Построение ROC-кривой по данным

При практическом построении ROC-кривой нам не нужно перебирать все вещественные пороги $\alpha$, поскольку мы работаем с конечной выборкой

$$(\mathbf{x}_1,y_1),(\mathbf{x}_2,y_2),...(\mathbf{x}_N,y_N).$$

Мы рассчитываем относительную дискриминантную функцию нашего классификатора $g(\mathbf{x})$ для каждого объекта и сортируем все объекты по возрастанию этой функции:

$$g\left(\mathbf{x}_{(1)}\right)\ge g\left(\mathbf{x}_{(2)}\right)\ge...\ge g\left(\mathbf{x}_{(N)}\right)$$

Далее ROC-кривая строится итеративно, стартуя из точки ($FPR_0,TPR_0$)=(0,0) при движении вдоль значений $g(\mathbf{x})$ справа-налево, перебирая в качестве пороговых $\alpha$ только следующие значения:

$$g\left(\mathbf{x}_{(N)}\right), g\left(\mathbf{x}_{(N-1)}\right),... g\left(\mathbf{x}_{(1)}\right), g\left(\mathbf{x}_{(1)}\right)-1$$

При переходе через объект положительного класса следующая точка ROC-кривой получается сдвигом вверх на $\frac{1}{N_+}$, поскольку на один верно-положительный объект стало больше, что повысит TPR на $\frac{1}{N_+}$ при том же уровне FPR.

А при переходе через отрицательный - сдвигом вправо на $\frac{1}{N_-}$, поскольку стало на один объект больше среди ложно-положительных срабатываний. FPR увеличится, а TPR останется неизменным.

Пример построения ROC-кривой показан на рисунке:

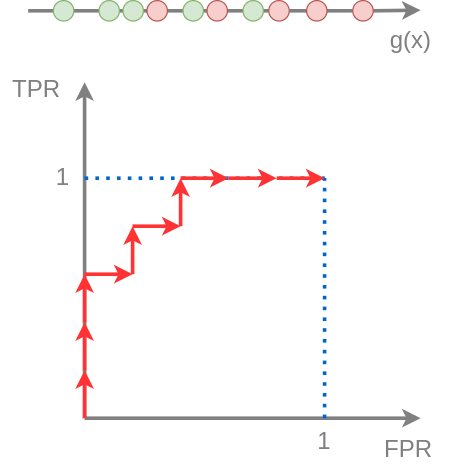
Далее ROC-кривая может сглаживаться линейной интерполяцией между точками.