Разложение на смещение и разброс

Разложение на смещение и разброс (bias-variance decomposition [1], впервые предложено в [2]) позволяет более формально описать недообучение (underfitting) и переобучение (overfitting) моделей машинного обучения.

Рассмотрим некоторую реальную задачу зависимость

y=f(\mathbf{x})+\varepsilon

где $y\in\mathbb{R}$ , $f(\mathbf{x})$ - некоторая функция, а $\varepsilon$ - случайный шум, не зависящий от объектов $\mathbf{x}$ и имеющий нулевой среднее.

Эту зависимость мы будем приближать модельной зависимостью $\widehat{f}(\mathbf{x})$ по имеющейся обучающей выборке

(X,Y)=\{(\mathbf{x}_{n},y_{n}),\,n=1,2...N\}

Зафиксируем объект $\mathbf{x}$ , для которого мы строим прогноз, и оценим ожидаемый квадрат ошибки $(\widehat{f}(\mathbf{x})-y(\mathbf{x}))^2$ , усредняя по реализациям случайного шума $\varepsilon$ и обучающей выборки $(X,Y)$ . Последнее представляет интерес, поскольку на практике в обучающую выборку попадают случайные объекты из генеральной совокупности.

Например, при классификации новостей мы выгружаем из интернета случайные $N$ новостей и их размечаем вручную. Но мы могли бы разметить и другие $N$ новостей, получив при этом другую обучающую выборку, по которой модель настроилась бы немного по-другому!

Лучшее, что мы можем сделать, это приблизить $\hat{f}(\mathbf{x})\approx f(\mathbf{x})$ , поскольку шум $\varepsilon$ не зависит от объектов и его мы прогнозировать не можем.

Разложение на смещение и разброс (bias-variance decomposition) декомпозирует ошибку прогноза на различные причины этой ошибки.

Разложение на смещение и разброс

\begin{aligned}\mathbb{E}_{X,Y,\varepsilon}\{[\widehat{f}(\mathbf{x})-y(\mathbf{x})]^{2}\}=&\left(\mathbb{E}_{X,Y}\{\widehat{f}(\mathbf{x})\}-f(\mathbf{x})\right)^{2}\\&+\mathbb{E}_{X,Y}\left\{ [\widehat{f}(\mathbf{x})-\mathbb{E}_{X,Y}\widehat{f}(\mathbf{x})]^{2}\right\} +\mathbb{E}\varepsilon^{2}\end{aligned}

Выражение в первой компоненте, возводимое в квадрат, называется смещением модели (bias) и показывает, насколько сильно модель будет систематически отклоняться от целевой зависимости $f(\mathbf{x})$ , если мы будем использовать различные обучающие выборки.
Вторая компонента разложения называется дисперсией модели (variance) и показывает, насколько сильно прогнозы модели будут различаться, если её настраивать на различных обучающих выборках.
Третья компонента называется неснижаемой ошибкой (irreducible error) и определяется шумом в данных, который мы предсказать не можем.

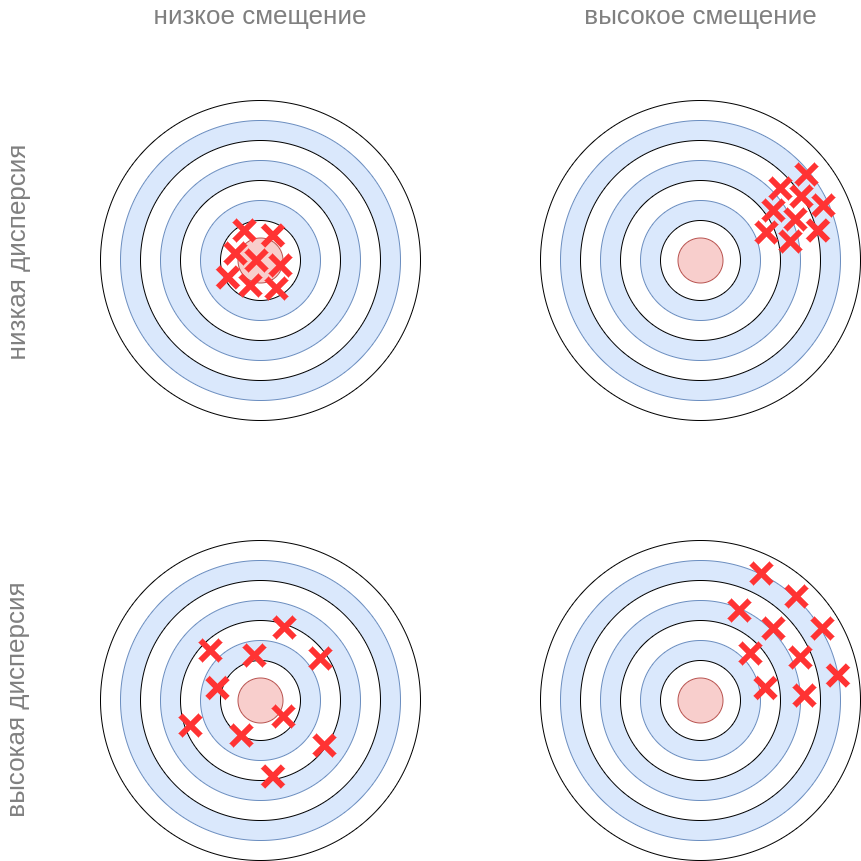
Это можно проиллюстрировать игрой в дартс, где мы стремимся попасть дротиком в центр цели. Ошибка попадания в цель может объясняться большим смещением (например, ветер систематически сдувает дротик в сторону) или большой дисперсией (неточные броски). Смещение и дисперсия могут присутствовать и совместно.

Рассмотрим задачу прогнозирования для квадратичной зависимости $y=x^2+\varepsilon$ .

У недообученных моделей (например, линейной регрессии от $y=w_0+w_1x$ ) ошибка будет вызвана высоким смещением, поскольку прямая будет систематически отклоняться от целевой квадратичной зависимости. При этом дисперсия модели будет невелика, поскольку в ней присутствуют всего два параметра $w_0,w_1$ и они будут примерно похожими для различных обучающих выборок.
У переобученных моделей (например, при прогнозировании квадратичной зависимости полиномом высокой степени или решающим деревом, которое мы строим до самого низа), напротив, смещение будет близким к нулю, поскольку они будут почти безошибочно подгоняться под обучающие данные, а ошибка прогнозирования будет вызвана высокой дисперсией, связанной с переобучением модели под конкретную реализацию обучающей выборки (модель её запоминает).

В следующей главе мы докажем разложение на смещение и разброс.

Разложение на смещение и разброс

Литература​

Литература