Нормализация признаков

Входные признаки в большинстве случаев будут иметь разный масштаб (диапазон изменения значений признака): одни признаки могут изменяться в диапазоне $[-0.01,0.01]$, другие в $[0,100]$ и т.д. Как мы впоследствии увидим из описаний методов машинного обучения, для большинства из них масштаб признаков будет оказывать влияние на прогноз. Для таких моделей чем выше разброс значений признака - тем сильнее он будет влиять на прогноз, перекрывая влияние других признаков.

Рассмотрим в качестве примера классификацию методом ближайшего соседа (nearest neighbor), который для каждого объекта $\mathbf{x}$ назначает тот класс, к которому принадлежит ближайший к нему объект из обучающей выборки. Для простоты рассмотрим классификацию на 2 класса (зелёный и красный) в двумерном пространстве признаков. Обучающая выборка состоит из двух объектов и требуется построить прогноз для точки в начале координат.

Исходная обучающая выборка приведена на рисунке слева.

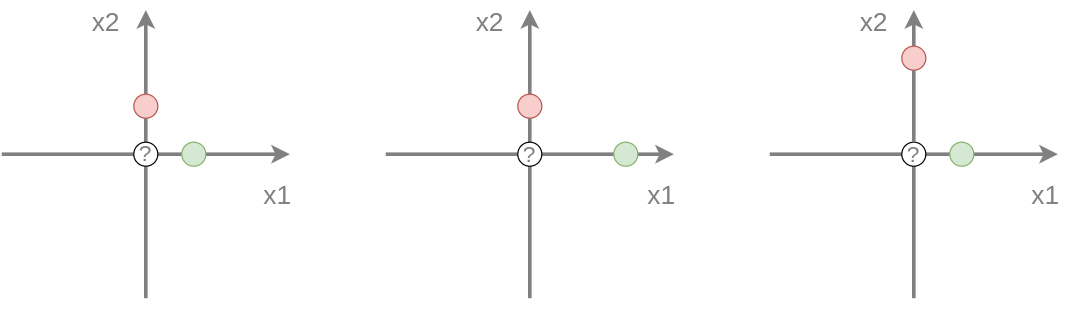
Как видим, обучающие объекты равноудалены от точки, для которой требуется сделать прогноз, поэтому оба класса равновероятны. Если мы умножим первый признак на два $x^1\to 2 x^1$, то прогнозом станет красный класс, как более близкий (в центре изображения). А если умножим на два второй признак $x^2\to 2 x^2$, то прогнозом будет зелёный класс (справа).

Чем выше разброс вдоль определённого признака, тем сильнее он влияет на прогноз, поэтому, чтобы влияние всех признаков было одинаковым, их необходимо нормализовать (привести к одному масштабу) одним из следующих способов:

Название	Преобразование	Выходные свойства
Стандартизация	$\frac{x^{j}-\mu_{j}}{\sigma_{j}}$	нулевое среднее и единичная дисперсия
Диапазонное шкалирование	$\frac{x^{j}-\min(x_{j})}{\max(x^{j})-\min(x^{j})}$	принадлежит интервалу [0,1]
Нормализация средним	$\frac{x^{j}-\mu_{j}}{\max(x^{j})-\min(x^{j})}$	нулевое среднее, с единичным диапазоном

Каждый вид шкалирования применяется независимо к каждому признаку (столбцу в матрице объекты-признаки X).

Самым популярным методом нормализации признака является стандартизация признака (standardization, standard scaler). Вторым по популярности является диапазонное шкалирование (min-max scaler). Оно хорошо тем, что значения признака из отрезка [0,MAX] переводятся в отрезок [0,1], причём ноль переходит в ноль, что полезно для разреженных данных (sparse data), в которых большинство значений - нули. Такие данные часто возникают на практике и эффективно кодируются разреженными матрицами (sparse matrix), которые их эффективно хранят и производят операции над ними, оперируя только ненулевыми элементами. Диапазонное шкалирование позволяет сохранить свойство разреженности.

Влияние выбросов

Наличие выбросов (аномально больших или малых значений) искажает результат нормализации, так наличие даже одного выброса может существенно сместить среднее, дисперсию, минимум или максимум. Поэтому важно предварительно отфильтровать выбросы из выборки. Либо применять робастную (устойчивую к выбросам) нормализацию, в которой используются другие статистики для оценки центра, разброса, минимума и максимума распределения:

неустойчивая статистика	робастный аналог	значение
$\frac{1}{N}\sum_{n=1}^N x^j$	$\text{median}\{x^j\}$	центр распределения
$\sqrt{\frac{1}{N}\sum_{n=1}^N (x^j_n)^2}$	$\text{median}\{\lvert x^j-\text{median}\{x^j\}\rvert\}$	разброс распределения
$\min$ $x^j$	1% перцентиль	минимум
$\max x^j$	99% перцентиль	максимум

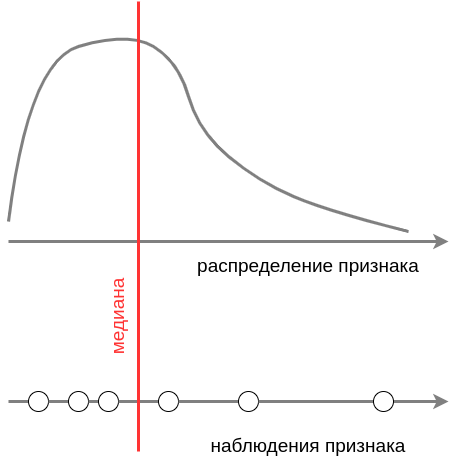
Медиана

Медиана (median) - метод, альтеранативный выборочному среднему (mean) для оценки центра распределения. Для выборки значений признака медиана - это такое значение, что половина наблюдений оказываются меньше, а другая половина - больше этого значения. Для вероятностного распределения медиана - это такое значение, что половина вероятностной массы лежит слева, а другая половина - справа от значения медианы.

p-процентная перцентиль

$p$-процентная перцентиль (percentile) - это такое значение, что

• для выборки наблюдений $p$ процентов наблюдений лежит слева, а $(1-p)$ процентов - справа от значения.

• для вероятностного распределения признак с вероятностью $p/100$ принимает значение меньше, а с вероятностью $(1-p)/100$ - больше значения перцентили.

$p$-квантиль - это по определению $(100*p)$-процентная перцентиль.