Предсказание вероятностей и преобразование SoftMax

Часто в прикладных задачах требуется хорошо предсказывать не только метку класса $\hat{y}\in\{1,2,...C\}$, но и вероятность каждого класса $p(c), c=1,2,...C.$ Например, в задачах прогноза погоды важно не только предсказать, будет ли ясная погода или дождь, но и вероятность дождя, поскольку даже если она меньше 50%, но близка к ней, то имеет смысл брать зонтик.

Для предсказания вероятностей классов нужно использовать их дискриминантные функции $g_c(\mathbf{x}), c=1,2,...C,$ характеризующие степень уверенности классификатора в том или ином классе. Поскольку дискриминантные функции могут принимать произвольные значения - как положительные, так и отрицательные, а сумма дискриминантных функций не обязательно равна единице, то к ним необходимо применить некоторое монотонно-возрастающее преобразование $F_{\tau}$, обеспечивающее два свойства:

• выходы должны быть неотрицательными,

• выходы должны суммироваться в единицу.

В качестве такого преобразования используют операцию SoftMax, используемую для перевода ненормированных рейтингов классов в их вероятности:

$$\begin{pmatrix} g_1(\mathbf{x}) \\ g_2(\mathbf{x}) \\ \cdots \\ g_C(\mathbf{x}) \\ \end{pmatrix} \longrightarrow \begin{pmatrix} \cfrac{e^{g_1(\mathbf{x})/\tau}}{\sum_{i=1}^C e^{g_i(\mathbf{x})/\tau}} \\ \cfrac{e^{g_2(\mathbf{x})/\tau}}{\sum_{i=1}^C e^{g_i(\mathbf{x})/\tau}} \\ \cdots \\ \cfrac{e^{g_C(\mathbf{x})/\tau}}{\sum_{i=1}^C e^{g_i(\mathbf{x})/\tau}} \\ \end{pmatrix} = \begin{pmatrix} \hat{p}(y=1|\mathbf{x}) \\ \hat{p}(y=2|\mathbf{x}) \\ \cdots \\ \hat{p}(y=C|\mathbf{x}) \\ \end{pmatrix}$$

Как вы думаете, на что влияет параметр $\tau$?

Параметр $\tau$, называемый температурой (temperature), определяет контрастность получаемых вероятностей. Чем $\tau$ выше, тем метод становится менее чувствительным к индивидуальным различиям дискриминантных функций, результирующее распределение вероятностей становится более близким к равномерному.

И наоборот, чем $\tau$ ниже, тем сильнее SoftMax реагирует на изменения рейтингов, а выходные вероятности становятся более контрастными.

Эти случаи показаны на рисунке:

Обобщение SoftMax-преобразования.

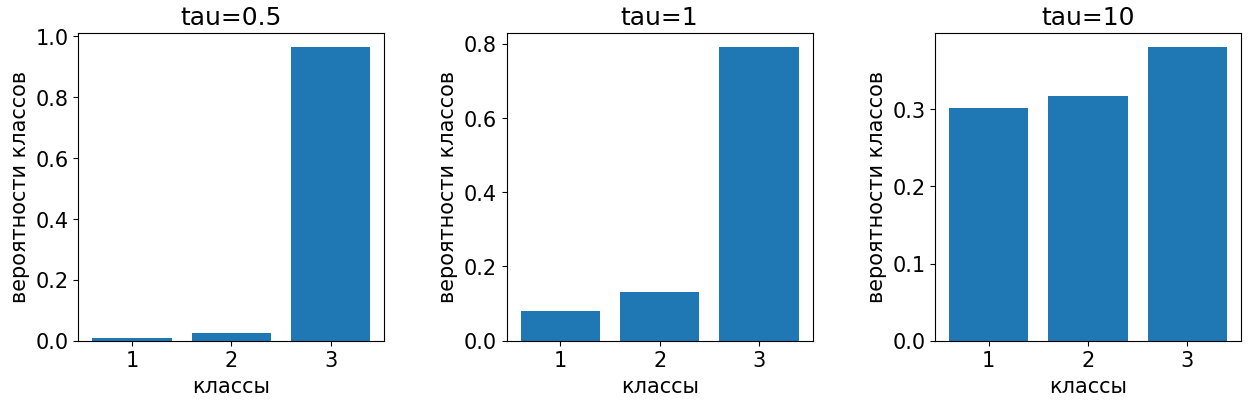
SoftMax-преобразование можно обобщить, применяя любую монотонно возрастающую функцию $F_{\tau}(\cdot)$, принимающую неотрицательные значения:

$$\begin{pmatrix} g_1(\mathbf{x}) \\ g_2(\mathbf{x}) \\ \cdots \\ g_C(\mathbf{x}) \\ \end{pmatrix} \longrightarrow \begin{pmatrix} \cfrac{F_{\tau}(g_1(\mathbf{x}))}{\sum_{i=1}^C F_{\tau}(g_i(\mathbf{x}))} \\ \cfrac{F_{\tau}(g_2(\mathbf{x}))}{\sum_{i=1}^C F_{\tau}(g_i(\mathbf{x}))} \\ \cdots \\ \cfrac{F_{\tau}(g_C(\mathbf{x}))}{\sum_{i=1}^C F_{\tau}(g_i(\mathbf{x}))} \\ \end{pmatrix} = \begin{pmatrix} \hat{p}(y=1|\mathbf{x}) \\ \hat{p}(y=2|\mathbf{x}) \\ \cdots \\ \hat{p}(y=C|\mathbf{x}) \\ \end{pmatrix} \tag{*}$$

В частном случае $F_\tau(g)=e^{g/\tau}$ получим операцию SoftMax.