Пулинг для последовательностей
Операция пулинга
Пулинг (pooling) - операция агрегации соседних значений последовательности или активаций свёртки, которая применяется для уменьшения длины промежуточного представления последовательности. Самые популярные - это максимизирующий и усредняющий пулинг.
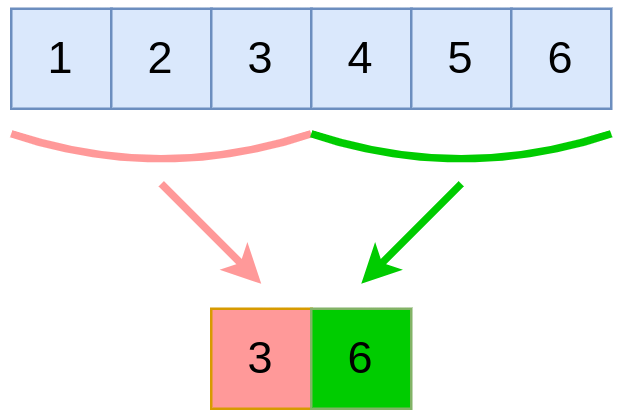
Максимизирующий пулинг (max pooling) агрегирует по области, возвращая максимальный элемент, как показано ниже для области из трёх соседних элементов:
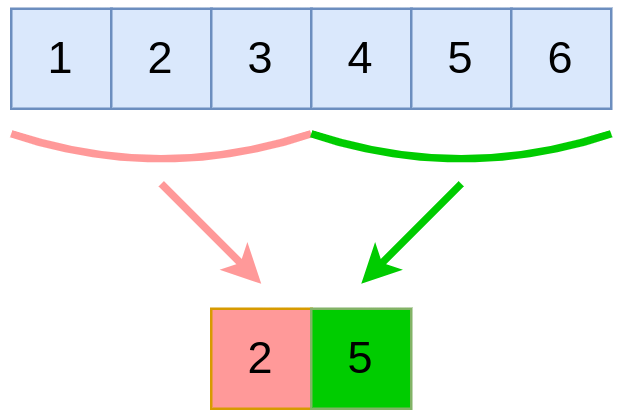
Усредняющий пулинг (average pooling) агрегирует по области, возвращая среднее значение элементов области, как показано ниже также для области из трёх соседних элементов:
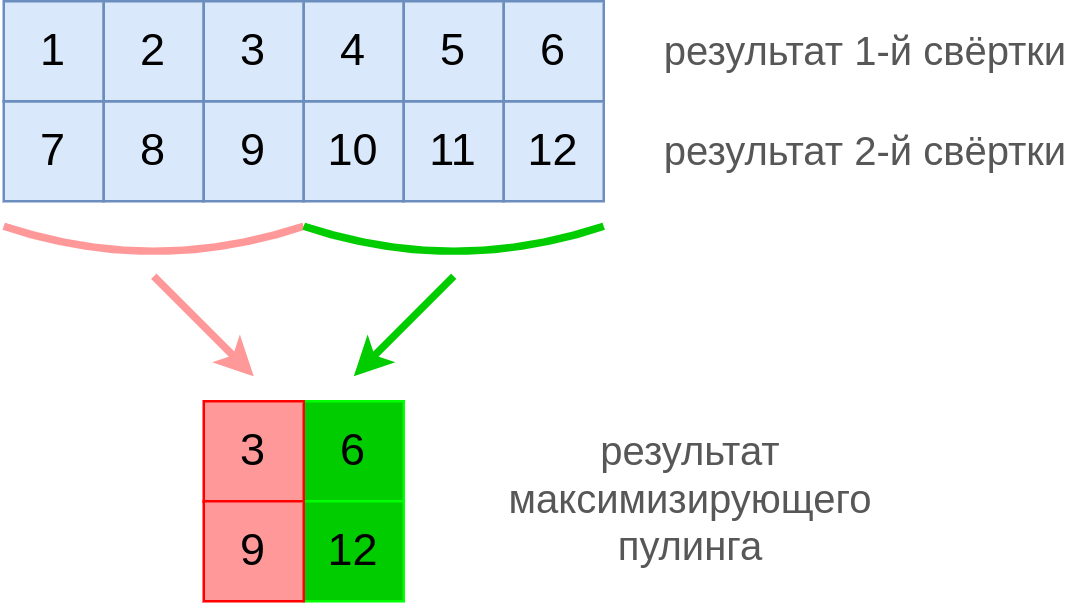
Если пулинг применяется к нескольким каналам (результатам действия нескольких свёрток), то он действует независимо для каждого канала:
Гиперпараметры
У пулинга отсутствуют настраиваемые параметры, но есть два гиперпараметра:
-
размер области, по которой производится агрегация (называется также размером ядра или kernel size). В примерах выше размер ядра был равен 3.
-
шаг смещения агрегируемой области для получения следующего выходного значения (stride). В примерах выше шаг был равен 3, и, как правило, его всегда выбирают равным размеру ядра.
Интуиция и преимущества пулинга
Пусть свёртка, к результатам которой применяется пулинг, извлекает некоторый признак.
Максимизирующий пулинг извлекает наличие интересуемого признака где-либо в агрегируемой области.
Усредняющий пулинг извлекает среднюю представленность интересуемого признака в агрегируемой области.
Обрабатываемые последовательности обычно имеют высокую размерность, и пулинг используется для того, чтобы эту размерность снизить. Например, пулинг с размером ядра 4 и сдвигом 4 уменьшит размерность выхода в 4 раза.
При обработке последовательностей существуют пулинги, которые возвращают не один, а сразу несколько значений агрегации. Например, top-1 и top-2 самых больших элемента в области.
Пулинг приближённо обеспечивает свойство инвариантности выходов нейросети к небольшим сдвигам. Например, если сдвинуть входную последовательность (с пролонгацией значений, то есть используя same padding) на примере ниже, то результат пулинга не изменится:
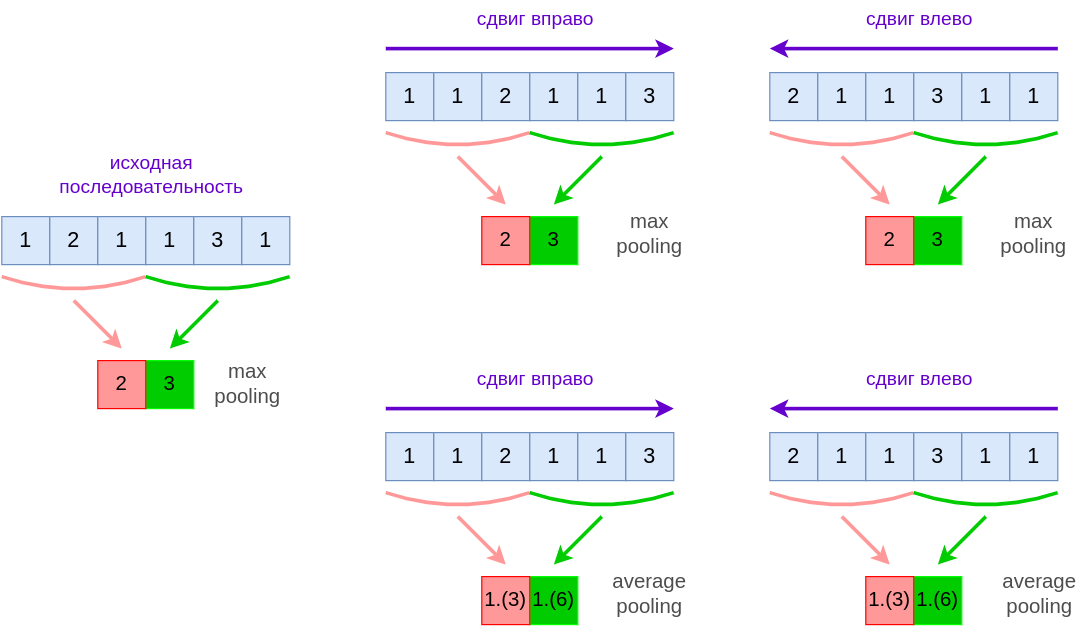
где 1.(3)=1.333..., а 1.(6)=1.666....
Пулинг обеспечивает лишь приближённую инвариантность к сдвигу. В случаях, когда резкие изменения происходят на границах агрегируемых областей, выходы пулинга могут существенно отличаться при сдвиге, однако это реализуется не так часто.
Построение эмбеддингов последовательности
Свёртка и пулинг, изученные ранее, переводят входную последовательность в выходную последовательность.
Часто возникает необходимость перевести последовательность произвольной длины в вектор фиксированного размера, называемый эмбеддингом последовательности (sequence embedding). Для этих целей используются глобальный и пирамидальный пулинг.
Глобальный пулинг
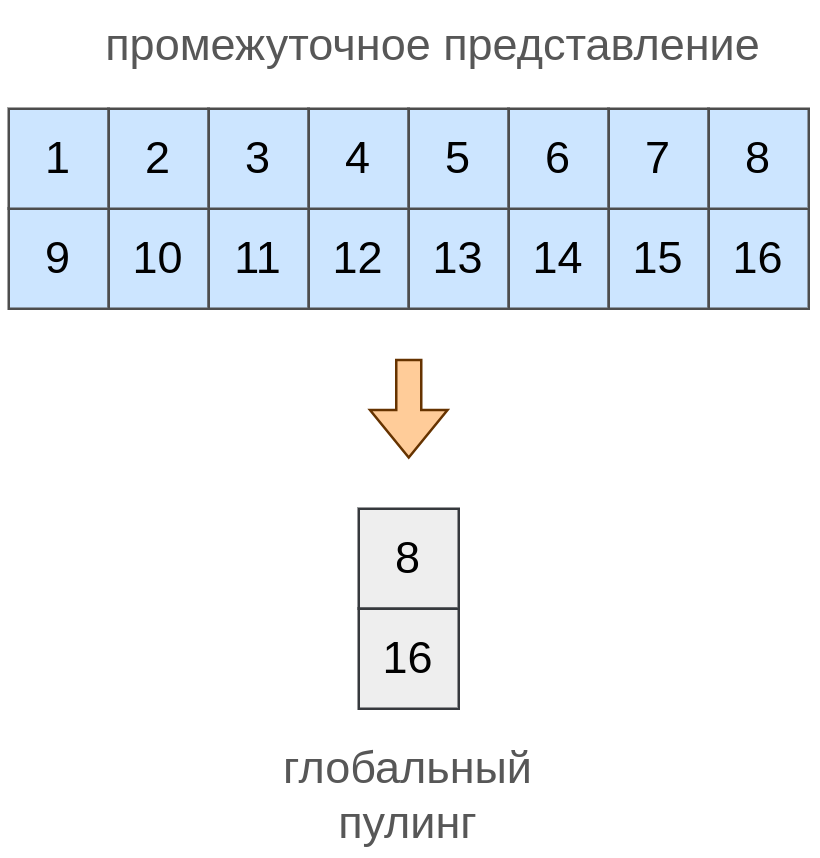
Глобальный пулинг (global pooling [1]) применяет агрегирующую операцию (усреднение или взятие максимума) ко всем значениям канала. А применяется он, как и обычный пулинг, к каждому каналу независимо. Таким образом, если свёрток предыдущего слоя сгенерировали последовательностей, то, применяя к каждой из них глобальный п�улинг, мы получим кодировку исходной последовательности произвольной длины -мерным вектором!
Если производить агрегацию взятием максимума, то получим глобальный максимизирующий пулинг (global max pooling), а если усреднением, то глобальный усредняющий пулинг (global average pooling).
Это удобно для последующей обработки последовательности многослойным персептроном, который ожидает на вход вектор признаков фиксированного размера.
Глобальный максимизирующий пулинг проиллюстрирован ниже (для двух каналов):
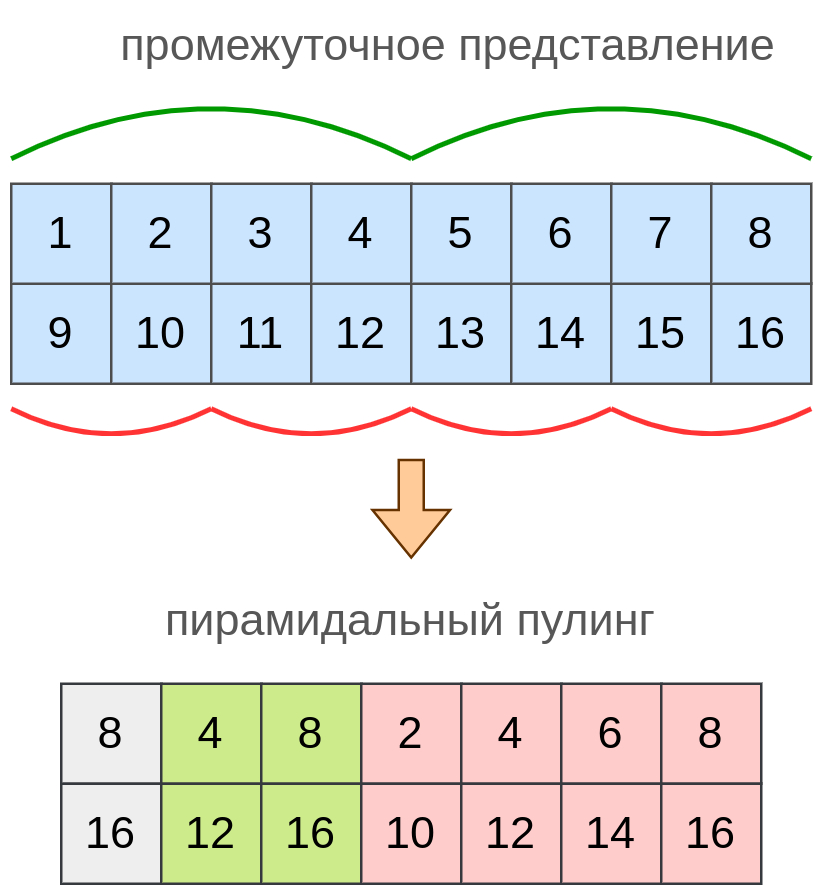
Пирамидальный пулинг
Глобальный пулинг успешно справляется с переводом последовательности произвольной длины в -мерный вектор. Однако при агрегации по всей длине последовательности полностью теряется пространственная информация о том, в каких именно участках достигались максимальные значения. Отчасти сохранить эту информацию позволяет пирамидальный пулинг (spatial pyramid pooling [2]), при котором последовательность вначале делится на блоков, и агрегация производится как глобальная, так и в рамках каждого блока, в результате чего каждый канал кодируется максимальными значениями для каждого из каналов. В результате входная последовательность произвольной длины кодируется -мерным вектором.
Ниже приведена работа максимизирующего пирамидального пулинга для двух каналов при . При таких настройках глобальный пулинг будет применяться сначала ко всей последовательности, з�атем к каждой из её половин, а потом к каждой из её четвертей, как показано на рисунке: