Свёртка для последовательностей

Операция свёртки

Пусть $\mathbf{x}=[x_1,x_2,...x_D]$ - обрабатываемая последовательность числовых значений.

Например, это может быть последовательность температур прибора, снимаемых каждые 10 секунд.

Свёртка (convolution) - это линейная операция, обладающая параметрами:

• $K=[K(-n),K(-n+1),...K(n-1),K(n)]\in\mathbb{R}^{2n+1}$ - ядро свёртки ( convolution kernel), обычно имеющая нечётный размеру (но может быть и чётным),

• смещение $b\in\mathbb{R}$.

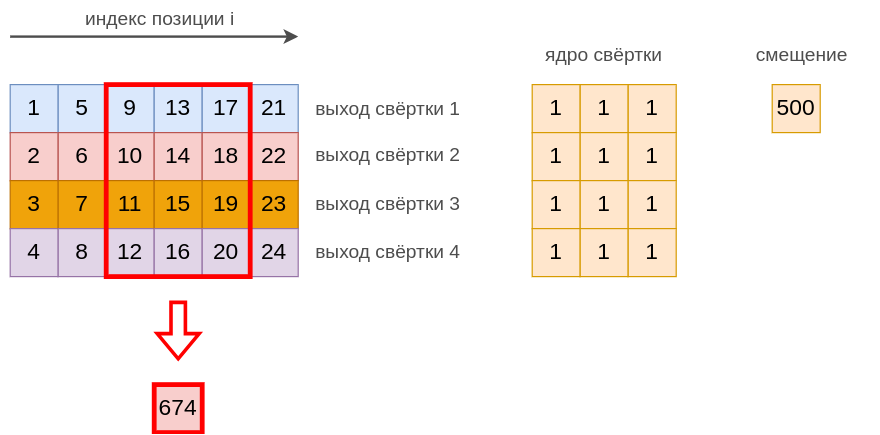
Выходом операции свёртки будет последовательность $y$ с элементами, считаемыми по формуле

$$y_j = \sum_{i=-n}^{n} K(i)x_{j+i}+b,\quad j=n+1,...D-n$$

Таким образом, свёртка генерирует последовательность, каждый элемент которой получается за счёт одного и того же линейного преобразования с $2n+2$ параметрами.

Рассмотрим пример вычисления свёртки для следующих данных:

Тогда выходной ряд будет строиться следующим образом:

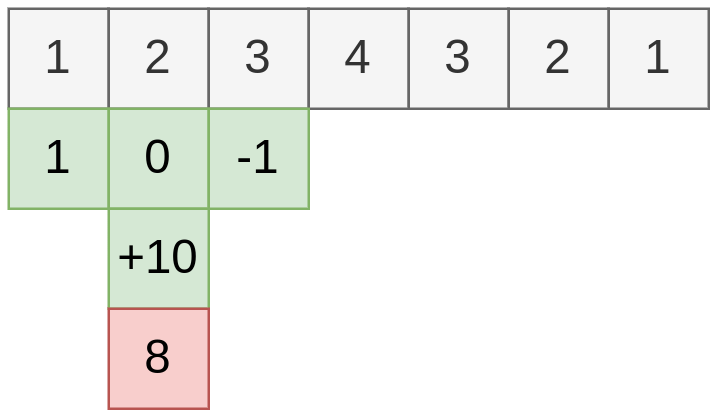
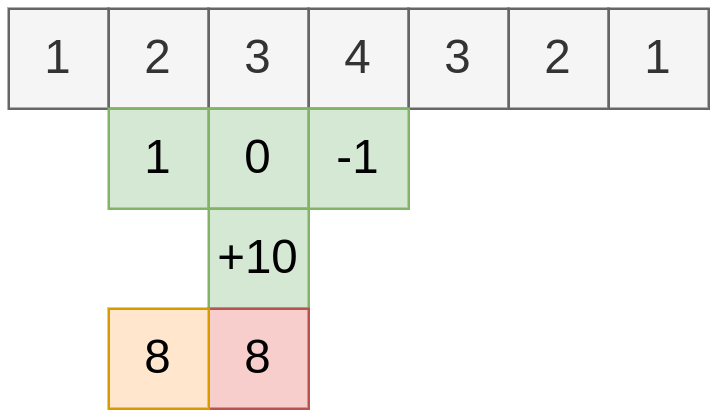
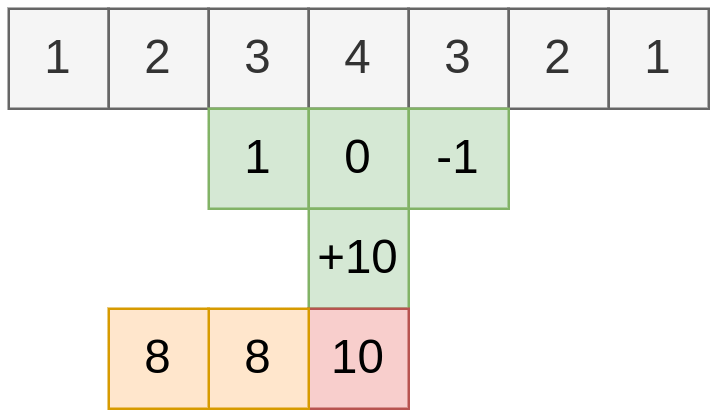
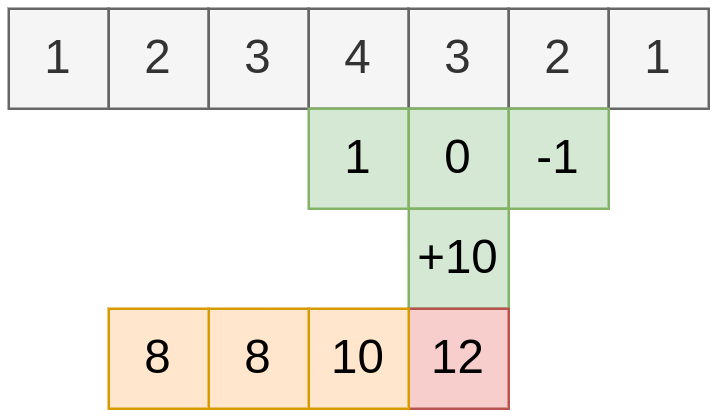
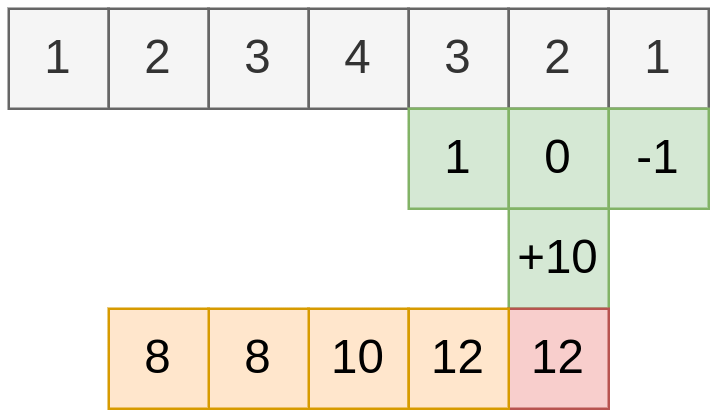
Примеры свёрток

Рассмотрим частные виды свёрток. Во всех примерах смещение $b$ равно нулю.

• $K=[\frac{1}{5},\frac{1}{5},\frac{1}{5},\frac{1}{5},\frac{1}{5}]$ отвечает равномерному усреднению, сглаживает временной ряд.

• $K=[0.1,0.2,0.4,0.2,0.1]$ - неравномерное усреднение, сглаживающее временной ряд, когда у центральных элементов вклад больше.

• $K=[-1,0,+1]$ вычисляет разностную производную $\Delta x_j = x_{j+1}-x_{j-1}$, то есть скорость изменения наблюдаемой величины.

• $K=[+1,-2,+1]$ вычисляет разностную вторую производную $\Delta x_j = (x_{j+1}-x_j)-(x_j-x_{j-1})$, то есть скорость изменения скорости наблюдаемой величины.

Автоматическая настройка

В ранних работах параметры свёрток подбирались вручную. Но если есть обучающая выборка, то эффективнее будет работать свёртка с автоматически настраиваемыми параметрами ядра и смещения - так операция будет лучше соответствовать данным и решаемой задаче.

Свойства свёртки

Свёртка извлекает один и тот же линейный признак, причём локально в каждой позиции. Это обеспечивает свойство эквивариантности к сдвигу (translation equivariance).

Сравнение свёртки с полносвязным слоем многослойного персептрона приведено ниже справа и слева соответственно (без смещений):

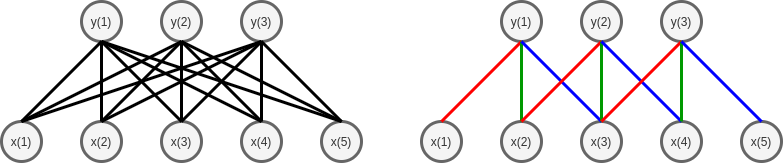
Как видим, свёртка предполагает существенно меньшее количество связей (sparse connections), что ускоряет вычисление и требует меньше параметров для обучения.

Дополнительное уменьшение параметров обеспечивается общностью весов (parameter sharing). На рисунке справа одинаковые веса обозначены одним цветом.

Свёртку можно применять к входным данным разной длины, причем число оцениваемых параметров будет одним и тем же - $2n+2$.

На многопроцессорных вычислительных устройствах, таких как видеокарта, вычисления производятся не последовательно один за другим, а параллельно, поэтому свёртка, вычисляемая независимо для разных позиций, считается очень быстро.

Также стоит обратить внимание, что выходная последовательность получается короче на $2n$, чем входная, поскольку ядро свёртки упирается в начало и конец входной временной последовательности.

Обработка динамического временного ряда

Обработка динамического временного ряда специфична тем, что наблюдения $x_1,x_2,...x_t$ поступают последовательно, а будущие наблюдения ещё неизвестны, когда нужно формировать выход $y_t$. Для такого рода данных свёртке разрешается использовать лишь последние располагаемые $n$ наблюдений:

$$y_t=\sum_{i=0}^{n-1} K(i)x_{t-i}+b,$$

а у самой свёртки остаются только $n+1$ параметров $K=[K(0),...K(n-1)]$ и $b$. Пример действия такой свёртки показан ниже:

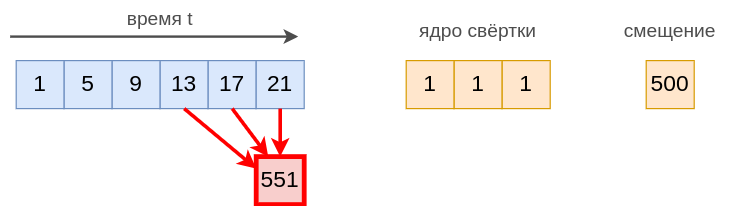
Такая свёртка может использоваться для прогнозирования будущих значений временного ряда.

Извлечение сложных нелинейных признаков

Наслаивая свёртки друг на друга, можно извлекать более сложные признаки с расширенной областью видимости (receptive field).

Ниже красным цветом показано, как результаты от более поздних свёрток зависят от более широкой окрестности значений входных данных:

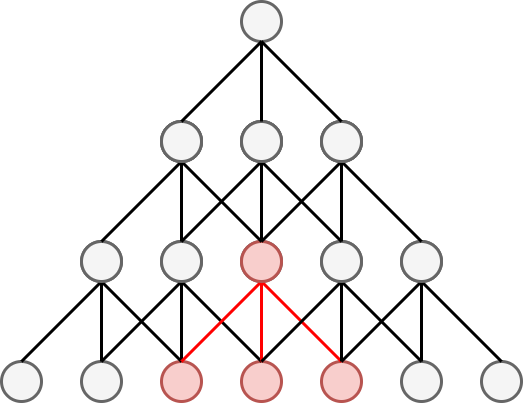
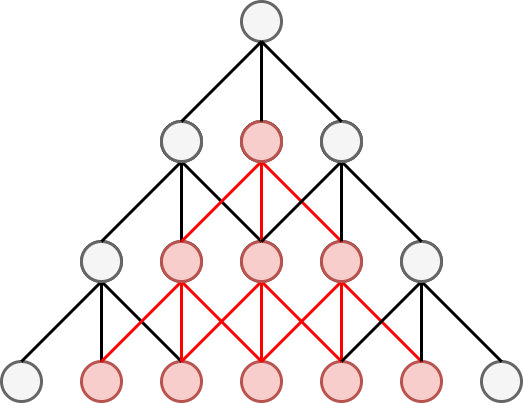
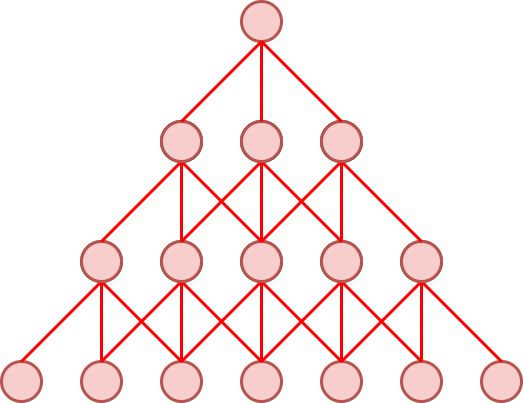
На каждом слое действует свёртка со своими индивидуальными параметрами.

Нелинейные признаки

Чтобы извлекаемые признаки получались нелинейными, после каждой свёртки применяют нелинейную функцию активации (иначе суперпозиция линейных функций снова даст линейную функцию!).

Суперпозиция свёрток с операциями нелинейности приводит к иерархичности признаковых представлений входной последовательности - более высокие слои будут извлекать более сложные признаки, зависящие от более широкой окрестности данных.

Чтобы извлечь более разнообразные признаки, на каждом слое применяют не одну, а сразу несколько свёрток (каждая - со своими параметрами):

$$\begin{aligned} y^1_j &= \sum_{i=-n}^{n} K^1(i)x_{j+i}+b^1 \\ y^2_j &= \sum_{i=-n}^{n} K^2(i)x_{j+i}+b^2 \\ \cdots \\ y^M_j &= \sum_{i=-n}^{n} K^M(i)x_{j+i}+b^M \end{aligned}$$

Тогда каждая свёртка следующего слоя будет определяться как локальная линейная комбинация результатов всех свёрток предыдущего слоя, и будет выполнять уже двумерную операцию:

$$z_j=\sum_{s=1}^M \sum_{i=-n}^n K(s,i)y^s_{j+i}+b$$

Графически это проиллюстрировано ниже: