Обработка графов

Рассмотрим основные задачи, которые решаются для данных, представимых в виде графа, с помощью нейронных сетей.

Понятие графа и его основные виды

Граф [1] в математике представляет собой коллекцию вершин (verteх) или узлов (node), соединённых друг с другом рёбрами (edge). Граф может быть направленным (directed graph) и ненаправленным (undirected graph) в зависимости от того, отношение связности действует в одну сторону или всегда в обе. Также граф может быть взвешенным (weighted graph), когда каждому ребру ставится в соответствие сила связи. Также ребрам можно ставить в соответствие и дискретные категории (тип связи) и вещественные признаки. Пример графа (источник):

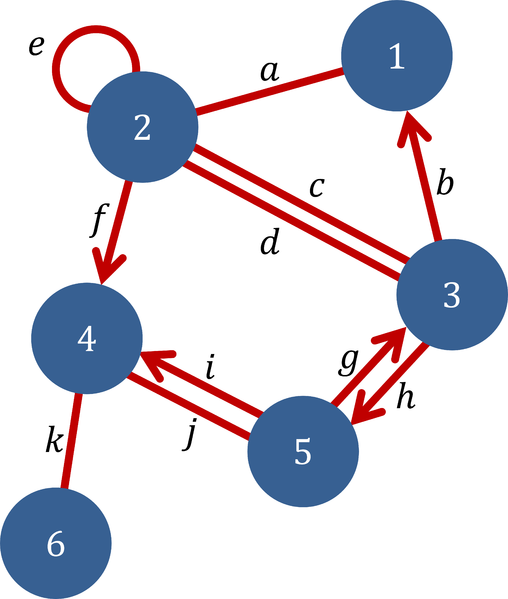
Примеры данных, представляемых в виде графа

Графы часто возникают на практике. Ниже приведены примеры данных, которые можно представить в виде графа:

социальная сеть, где узлами выступают люди, а связи - добавил ли человек другого человека в друзья или писал ли ему сообщения;
интернет, где узлами выступают веб-страницы, а связи отражают ссылки одних веб-страниц на другие;
научные публикации, где узлами выступают статьи, а рёбра проводятся, если одна статья ссылается на другую;
компьютерная сеть, где узлами выступают компьютеры и сетевые устройства, а ребра проводятся, если устройства соединены и посылают друг другу данные;
знания, где узлами выступают сущности, а ребра отражают связи между этими сущностями, как показано ниже (источник):
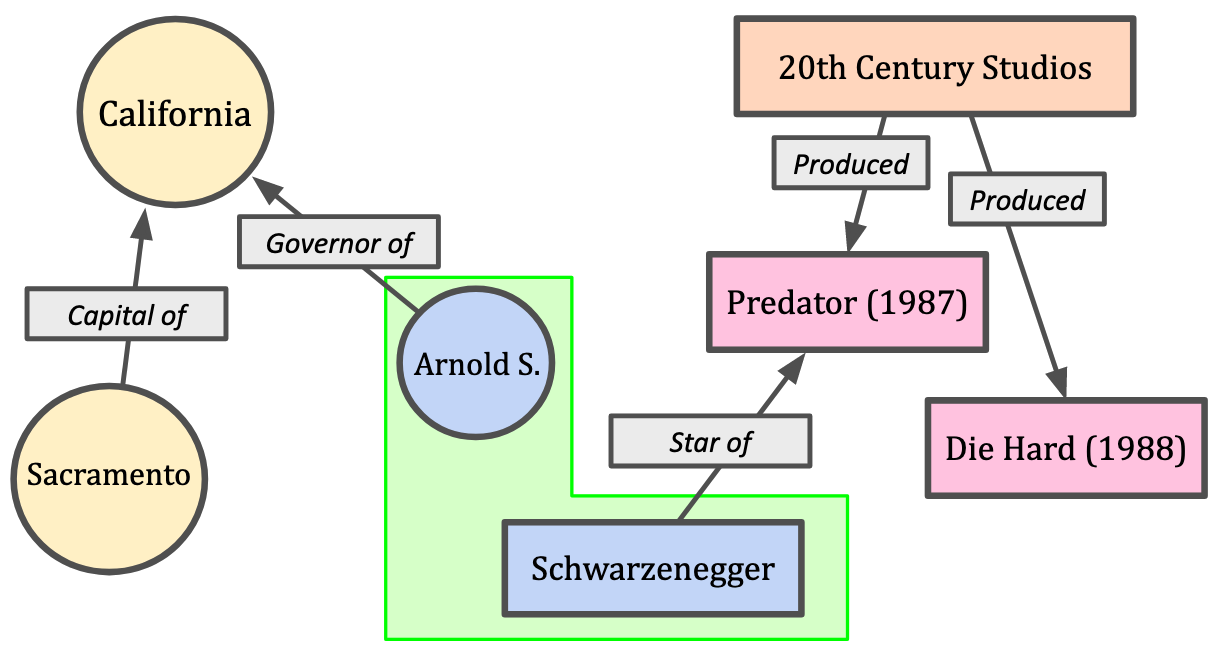
вещества, где узлами выступают молекулы, а связями - их химические соединения (источник):

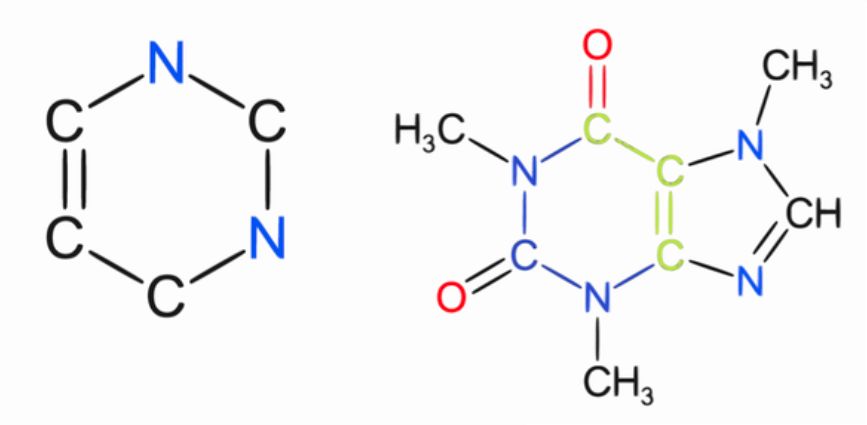
Задачи на графах, решаемый нейросетями

Опишем основные задачи, которые можно решать на графах с помощью нейросетей.

Классификация графа (graph classification [2]) - отнесение графа к одному из дискретных классов. Например, по химическому соединению лекарства предсказать, будет ли оно обладать лечебным эффектом. Также можно решать и задачу регрессии (graph regression [3]), например, по виду химического соединения определить его температуру плавления.

Классификация узлов графа (node classification [4]). Например, для графа социальной сети определять, является ли аккаунт ботом или реальным человеком.

Восстановление ребер на графе (link prediction [5]). Например, в графе научных работ предсказывать недостающие ссылки на связанные научные исследования.

Можно решать задачу классификации и регрессии на ребрах графа (edge classification / edge regression). Например, в графе социальной сети предсказывать, как часто друзья будут обмениваться сообщениями и будут ли посылать друг другу изображения, приглашать в группы и т.д.

Генерация графа, обладающего требуемыми свойствами (graph generation [6]). Например, нас может интересовать список химических соединений, обладающих как высокой прочностью, так и низкой плотностью для авиапромышленности. Либо в медицине интересны лекарственные вещества, обладающие максимальным лечебным действием при минимуме побочных эффектов.

Прогнозирование изменений во времени (dynamic / temporal graph prediction [7]). Например, предсказание, как будет эволюционировать социальная сеть, какие связи появятся или исчезнут в будущем, или как изменится структура молекулы при воздействии внешней среды.

Кластеризация графа (graph clustering [8]). Например, выделение сообществ пользователей в социальной сети, выявление функциональных групп атомов в молекуле или модулей в биологических сетях.

Сопоставление графов (graph matching / graph similarity [9]). Например, определение степени схожести двух химических соединений или поиск похожих подструктур в базе графов научных публикаций.

Обработке графов нейросетевыми методами посвящён отдельный раздел учебника.

Обработка графов

Понятие графа и его основные виды​

Примеры данных, представляемых в виде графа​

Задачи на графах, решаемый нейросетями​

Литература​

Понятие графа и его основные виды

Примеры данных, представляемых в виде графа

Задачи на графах, решаемый нейросетями

Литература