Снижение размерности методом LDA

Ранее мы изучили линейный дискриминантный анализ (Linear Discriminant Analysis, LDA) как вероятностную модель, основанную на предположении о нормальном распределении признаков внутри каждого класса с общей ковариационной матрицей $\Sigma$:

$$p(\boldsymbol{x} | y) = \frac{1}{(2\pi)^{D/2} |\Sigma|^{1/2}} \exp \left( -\frac{1}{2} (\boldsymbol{x} - \boldsymbol{\mu}_y)^T \Sigma^{-1} (\boldsymbol{x} - \boldsymbol{\mu}_y) \right)$$

Однако популярность этого метода обусловлена не только его свойствами классификатора, но и возможностью строить информативные проекции данных в пространство низкой размерности в режиме обучения с учителем (supervised), то есть учитывая метки классов.

Учёт меток позволяет находить направления, проекции на которые лучше дискриминируют классы, как показано на рисунке ниже, на котором показана главная компонента, извлечённая методом LDA и PCA:

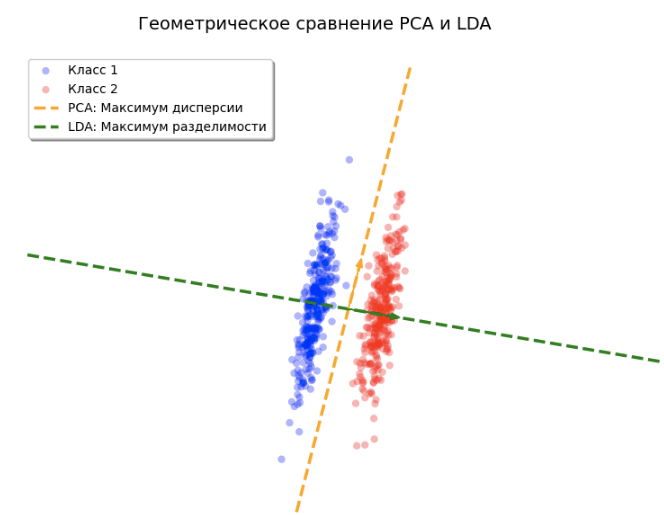
Главная компонента метода PCA учитывает только направления максимального разброса признаков, что не всегда сочетается с качеством разделения классов, как в приведённом случае.

Геометрия ближайших центроидов

Рассмотрим дискриминантную функцию LDA, полученную на промежуточном этапе вывода в прошлой главе:

$$g_y(\boldsymbol{x}) = -\frac{1}{2} (\boldsymbol{x} - \boldsymbol{\mu}_y)^T \Sigma^{-1} (\boldsymbol{x} - \boldsymbol{\mu}_y) + \ln p(y)$$

Здесь выражение $(\boldsymbol{x} - \boldsymbol{\mu}_y)^T \Sigma^{-1} (\boldsymbol{x} - \boldsymbol{\mu}_y)$ представляет собой квадрат расстояния Махаланобиса (Mahalanobis distance) между точкой $\boldsymbol{x}$ и центроидом класса $\boldsymbol{\mu}_y$.

Таким образом, LDA можно интерпретировать как метод ближайшего центроида (nearest centroid method), где расстояние измеряется с учётом корреляционной структуры данных ($\Sigma$), а выбор класса корректируется на априорную вероятность (prior probability) $p(y)$.

Декорреляция данных

Расстояние Махаланобиса кажется сложным, но его легко свести к обычному евклидову расстоянию через преобразование декорреляции (decorrelation):

$$\boldsymbol{x}^* = \Sigma^{-1/2} \boldsymbol{x}$$

Покажем, что в новом декоррелированном пространстве после указанного преобразования расстояние становится евклидовым:

$$d_{\Sigma}^2(\boldsymbol{x}, \boldsymbol{\mu}_y) = (\boldsymbol{x} - \boldsymbol{\mu}_y)^T \Sigma^{-1} (\boldsymbol{x} - \boldsymbol{\mu}_y)$$ $$= (\boldsymbol{x} - \boldsymbol{\mu}_y)^T (\Sigma^{-1/2})^T \Sigma^{-1/2} (\boldsymbol{x} - \boldsymbol{\mu}_y)$$ $$= (\Sigma^{-1/2}(\boldsymbol{x} - \boldsymbol{\mu}_y))^T (\Sigma^{-1/2}(\boldsymbol{x} - \boldsymbol{\mu}_y)) = \|\boldsymbol{x}^* - \boldsymbol{\mu}_y^*\|^2$$

Геометрическая интерпретация

Декоррелирующее преобразование $\Sigma^{-1/2}$ преобразует пространство таким образом, что эллипсоидальное облако исходных объектов превращается в распределение точек внутри сферы. Далее в этом пространстве вычисляется обычное евклидово расстояние.

Декоррелирование вектров-строк

Если $\boldsymbol{x}$ - вектор-строка (а не столбец, как обычно), то декоррелирующее преобразование будет получаться транспонированием:

$$\boldsymbol{x} = \boldsymbol{x} \Sigma^{-1/2}$$

Мы воспользовались свойством $(\Sigma^{-1/2})^T=\Sigma^{-1/2}$ для симметричном матрицы $\Sigma$.

Неявное снижение размерности

Важной особенностью LDA является скрытое снижение размерности. Если у нас есть $C$ центроидов $\boldsymbol{\mu}_1, \dots, \boldsymbol{\mu}_C$ в $D$-мерном пространстве, то они всегда лежат в некотором аффинном подпространстве размерности не более $C-1$.

При поиске ближайшего центроида (в сферическом пространстве) мы можем полностью игнорировать любые отклонения объекта, которые перпендикулярны этому подпространству, так как они вносят одинаковый вклад в расстояние до каждого класса. Следовательно, для работы LDA достаточно рассматривать данные только в подпространстве размерности $C-1$.

Метод проекций (Reduced-Rank LDA)

Если нам нужно снизить размерность до уровня $K < C-1$ (например, до $K=2$ для визуализации), мы должны выбрать наиболее информативное подпространство. Будем считать таким то подпространство, в котором проекции центроидов максимально разнесены с учётом мощности каждого центроида (числа объектов в соответствующем классе).

Для этого применяется метод главных компонент (PCA), но для центроидов с учётом их веса (числа объектов в соответствующем кластере):

1. Находится общая матрица ковариации $\Sigma$ исходных данных.
2. Вычисляется матрица центроидов $M\in\mathbb{R}^{C \times D}$.
3. Проводится декорреляция центроидов: $M^* = M \Sigma^{-1/2}$.
4. Вычисляется межклассовая матрица разброса $B^*$ для трансформированных средних с учётом частотности классов $\pi_y = p(y)$:

$$B^* = \sum_{y=1}^C \pi_y (\boldsymbol{\mu}_y^* - \bar{\boldsymbol{\mu}}^*)(\boldsymbol{\mu}_y^* - \bar{\boldsymbol{\mu}}^*)^T$$

Здесь $\bar{\boldsymbol{\mu}}^* = \sum \pi_y \boldsymbol{\mu}_y^*$ — общее среднее в новом пространстве.

Затем находится $K$ собственных векторов $\boldsymbol{v}^*_{k}$, $k=1,2,...K$ матрицы $B^*$, отвечающих $K$ максимальным собственным значениям (главные компоненты). Эти векторы определяют направления в декоррелированном пространстве, вдоль которых центроиды классов имеют максимальный разброс.

Ограничение на количество компонент

Метод LDA позволяет извлечь не более $C-1$ информативных направлений, поскольку справедливо следующее утверждение:

Утверждение:

Ранг матрицы $B^* = \sum_{y=1}^C \pi_y (\boldsymbol{\mu}_y^* - \bar{\boldsymbol{\mu}}^*)(\boldsymbol{\mu}_y^* - \bar{\boldsymbol{\mu}}^*)^T$ не превосходит $C-1$.

Доказательство:

Матрица $B^*$ является суммой $C$ внешних произведений векторов вида $(\boldsymbol{\mu}_y^* - \bar{\boldsymbol{\mu}}^*)$. Заметим, что по определению общего среднего $\bar{\boldsymbol{\mu}}^* = \sum \pi_y \boldsymbol{\mu}_y^*$ выполняется условие:

$$\sum_{y=1}^C \pi_y (\boldsymbol{\mu}_y^* - \bar{\boldsymbol{\mu}}^*) = \sum \pi_y \boldsymbol{\mu}_y^* - \bar{\boldsymbol{\mu}}^* \sum \pi_y = \bar{\boldsymbol{\mu}}^* - \bar{\boldsymbol{\mu}}^* = \boldsymbol{0}$$

Это означает, что векторы отклонений центроидов линейно зависимы. Следовательно, подпространство, натянутое на эти векторы, имеет размерность не более $C-1$. Ранг матрицы $B^*$ (количество её ненулевых собственных чисел) также ограничен этой величиной.

$\square$

Практическое следствие

Если в вашей задаче всего 2 класса (бинарная классификация), LDA всегда предложит только одну главную компоненту (проекцию на прямую), даже если исходных признаков тысячи. Для визуализации данных в 2D (на плоскости) методом LDA требуется наличие как минимум 3-х классов.

Направления в исходном пространстве

Чтобы спроецировать исходный объект $\boldsymbol{x}$ на $k$-ю дискриминантную ось, нам нужно найти соответствующий вектор весов $\boldsymbol{v}_{k}$ в исходном признаковом пространстве.

Как было показано ранее, результат проекции $z_{k}$ в сферическом пространстве равен:

$$z_{k} = (\boldsymbol{v}^*_{k})^T \boldsymbol{x}^* = (\boldsymbol{v}^*_{k})^T \Sigma^{-1/2} \boldsymbol{x} = (\Sigma^{-1/2}\boldsymbol{v}^*_{k})^T \boldsymbol{x}$$

Следовательно, искомый вектор направления выражается формулой:

$$\boldsymbol{v}_{k} = \Sigma^{-1/2} \boldsymbol{v}^*_{k}$$

Свойства метода

Векторы $\boldsymbol{v}^*_1, \dots, \boldsymbol{v}^*_K$, будучи главными компонентами в декоррелированном пространстве, имеют единичную норму и взаимно ортогональны:

$$(\boldsymbol{v}^*_i)^T \boldsymbol{v}^*_j = \mathbb{I}\{i=j\}$$

Однако это свойство не сохраняется для соответствующих дискриминантных направлений $\boldsymbol{v}_k$ в исходном пространстве.

Визуально в исходном пространстве оси LDA могут выглядеть как пересекающиеся под произвольным углом. Это происходит потому, что LDA «подстраивается» под эллиптическую форму облака данных.

Таким образом, при переходе к исходным признакам мы жертвуем привычной евклидовой ортонормированностью векторов ради сохранения сильных дискриминирующих свойств новых признаков.

Однако для этих векторов справедливо следующее свойство:

$$\begin{aligned} \boldsymbol{v}_i^T \Sigma \boldsymbol{v}_j &= (\Sigma^{-1/2} \boldsymbol{v}^*_i)^T \Sigma (\Sigma^{-1/2} \boldsymbol{v}^*_j) \\ &= (\boldsymbol{v}^*_i)^T (\Sigma^{-1/2})^T \Sigma \Sigma^{-1/2} \boldsymbol{v}^*_j \\ &= (\boldsymbol{v}^*_i)^T \Sigma^{-1/2} \Sigma \Sigma^{-1/2} \boldsymbol{v}^*_j \\ &= (\boldsymbol{v}^*_i)^T I \boldsymbol{v}^*_j = \mathbb{I}\{i=j\} \end{aligned}$$

Отсюда следует следующее важное свойство проекций на дискриминантные направления:

Утверждение: нескоррелированность признаков

Новые признаки $z^i$, полученные путём проекции центрированных данных на дискриминантные направления $\boldsymbol{v}_i$, нескоррелированы между собой и имеют единичную дисперсию.

Доказательство:

Рассмотрим ковариацию между двумя новыми признаками $z^i$ и $z^j$. Поскольку исходные признаки центрированы ($\mathbb{E}[\boldsymbol{x}] = \boldsymbol{0}$), математическое ожидание проекций также равно нулю: $\mathbb{E}[z^i] = \mathbb{E}[\boldsymbol{v}_i^T \boldsymbol{x}] = 0$.

Тогда ковариация записывается как:

$$\text{cov}(z^i, z^j) = \mathbb{E}[z^i z^j] = \mathbb{E}[(\boldsymbol{v}_i^T \boldsymbol{x})(\boldsymbol{x}^T \boldsymbol{v}_j)]$$

Воспользуемся линейностью математического ожидания и вынесем векторы весов за знак оператора:

$$\text{cov}(z^i, z^j) = \boldsymbol{v}_i^T \mathbb{E}[\boldsymbol{x} \boldsymbol{x}^T] \boldsymbol{v}_j = \boldsymbol{v}_i^T \Sigma \boldsymbol{v}_j$$

Используя ранее доказанное свойство $\boldsymbol{v}_i^T \Sigma \boldsymbol{v}_j = \mathbb{I}\{i=j\}$, получаем:

$$\text{cov}(z^i, z^j) = \mathbb{I}\{i=j\}$$

Таким образом, при $i \neq j$ ковариация (а значит, и корреляция) равна нулю. При $i = j$ дисперсия каждого нового признака равна единице.

$\square$