Метод главных компонент

Новые признаки как проекции

В машинном обучении мы привыкли работать с исходными признаками объекта $\boldsymbol{x} = (x^1, x^2, \dots, x^D)^T$. Однако часто гораздо полезнее рассматривать не сами значения признаков, а их линейные комбинации. Любую такую комбинацию можно представить как скалярное произведение вектора объекта $\boldsymbol{x}$ на некоторый вектор весов $\boldsymbol{v}$:

$$z = \sum_{i=1}^D v^i x^i = \langle \boldsymbol{x}, \boldsymbol{v} \rangle = \boldsymbol{v}^T \boldsymbol{x}$$

Рассмотрим примеры того, как линейные комбинации позволяют извлекать смысл из данных:

1. Средняя оценка: Если $\boldsymbol{x} = [5, 4, 3, 5, 4]$ — оценки студента по 5 предметам, а $\boldsymbol{v} = [1/5, 1/5, 1/5, 1/5, 1/5]^T$, то $z$ равен среднему баллу.

2. Разница стоимостей: Если $\boldsymbol{x} = [p_{today}, p_{yesterday}]$ — цены акции, а $\boldsymbol{v} = [1, -1]^T$, то $z$ характеризует суточное изменение цены.

3. Суммарная активность: Если $\boldsymbol{x}$ — количество действий пользователя в разные часы суток, значение $z$ покажет общую интенсивность за сутки.

4. Цветовой баланс: В обработке изображений проекция RGB-вектора на $[0.299, 0.587, 0.114]^T$ позволяет перевести цветной пиксель в яркость (оттенки серого).

Если мы ограничим вектор $\boldsymbol{v}$ условием единичной нормы ($\|\boldsymbol{v}\|=1$), то значение проекции $z$ объекта $\boldsymbol{x}$ на него можно удобно находить как скалярное произведение:

$$z = \boldsymbol{x}^T \boldsymbol{v} = \langle \boldsymbol{x}, \boldsymbol{v}\rangle$$

Почему так?

Это утверждение опирается на определение скалярного произведения и тригонометрию в прямоугольном треугольнике. Разберём это подробнее.

Скалярное произведение двух векторов $\boldsymbol{x}$ и $\boldsymbol{v}$ можно выразить через их длины и косинус угла $\theta$ между ними:

$$z = \langle \boldsymbol{x}, \boldsymbol{v} \rangle = \|\boldsymbol{x}\| \cdot \|\boldsymbol{v}\| \cdot \cos \theta$$

Если мы наложим условие единичной нормы на вектор $\boldsymbol{v}$, то есть $\|\boldsymbol{v}\| = 1$, формула упрощается:

$$z = \|\boldsymbol{x}\| \cdot \cos \theta$$

Последнее выражение как раз и равно длине проекции (со знаком, в зависимости от направления векторов).

Возникает вопрос: какие именно вектора $\boldsymbol{v}$ обеспечивают максимальное сохранение информации об исходных данных?

Метод главных компонент (Principal Component Analysis, PCA) решает эту задачу, предлагая последовательно находить направления, вдоль которых данные сохраняют наибольшую изменчивость.

Определение и свойства

Индивидуально каждая $k$-я главная компонента (Principal Component) определяется как направление $\boldsymbol{v}_k$, которое обеспечивает максимум дисперсии проекций данных на него при условии, что этот вектор ортогонален всем ранее найденным компонентам $\boldsymbol{v}_1, \dots, \boldsymbol{v}_{k-1}$.

Линейная оболочка первых $K$ главных компонент образует $K$-мерное подпространство наилучшей аппроксимации. Оно является оптимальным в глобальном смысле: среди всех возможных подпространств размерности $K$ именно это подпространство лучше всего описывает структуру исходных данных, максимизируя средний квадрат длин проекций на него и минимизируя средний квадрат длин ошибок аппроксимации исходных объектов их проекциями.

Метод порождает новое признаковое описание объектов в виде длин проекций объекта на первые $K$ главных компонент, компактно и информативно описывающих исходные данные.

Новые признаки обладают удобными свойствами:

• они являются нескоррелированными;
• они обладают свойством линейной независимости.

Это упрощает настройку последующих моделей на этих признаках, делая её более стабильной.

Аналитический вид главных компонент

Главные компоненты представляют собой собственные векторы $\boldsymbol{v}_1, \dots, \boldsymbol{v}_D$ матрицы $\Sigma$, которая является ковариационной матрицей признаков, предварительно центрированных относительно их среднего значения. При этом каждое соответствующее собственное значение (eigenvalue) $\lambda_k$ характеризует величину дисперсии (информативности), сосредоточенной вдоль выбранной компоненты.

Алгоритм применения

Процедура применения PCA на практике выглядит следующим образом:

1. Центрирование данных:

$$\boldsymbol{x}_n \leftarrow \boldsymbol{x}_n - \boldsymbol{\mu}$$

2. Вычисление ковариационной матрицы $\Sigma$ и её спектральное разложение:

$$\Sigma = \frac{1}{N} \sum_{n=1}^N \boldsymbol{x}_n \boldsymbol{x}_n^T = V \Lambda V^T$$

3. Переход к новым признакам:

$$\boldsymbol{z}_n = V_K^T \boldsymbol{x}_n$$

где $V_K$ — матрица, составленная из первых $K$ столбцов матрицы собственных векторов $V$ (первые $K$ главных компонент).

Аппроксимации в исходном признаковом пространстве

Если требуется получить вектор аппроксимации $\hat{\boldsymbol{x}}_n$, извлекаемый по первым $K$ главным компонентам исходного вектора $\boldsymbol{x}_n$, это можно сделать, вернувшись из базиса главных компонент в исходное признаковое пространство по следующей формуле:

$$\hat{\boldsymbol{x}}_n = \boldsymbol{\mu} + V_K \boldsymbol{z}_n = \boldsymbol{\mu} + \sum_{i=1}^K z_n^i \boldsymbol{v}_i$$

Это может быть полезным, например, для в задачах фильтрации данных от шума.

Применение метода на практике

Метод главных компонент (Principal Component Analysis, PCA) находит широкое применение в анализе данных, когда необходимо упростить структуру признакового пространства, сохранив при этом максимум полезной информации.

Рассмотрим основные способы его использования:

1. Визуализация данных: При $K=2$ или $K=3$ многомерные объекты можно отобразить на плоскости или в пространстве. Это позволяет визуализировать многомерные данные, увидеть на них кластеры, аномалии и общие закономерности.

2. Сжатие данных: Метод позволяет хранить основную информацию о многомерных объектах, используя небольшое число признаков. Например, в алгоритме Eigenfaces изображения человеческих лиц компактно представляются в комбинации небольшого числа «эталонных» лиц.

3. Фильтрация шума (noise filtering): Считается, что компоненты с очень малыми собственными числами $\lambda_i$ описывают случайный шум. Отбрасывая их, мы очищаем сигнал от помех.

4. Предварительная обработка: Метод главных компонент часто используется перед применением регрессионных моделей или нейросетей. Он решает проблему мультиколлинеарности признаков (ситуации, когда признаки сильно коррелируют друг с другом), вызывающей неустойчивости настройки весов модели.

5. Компактное информативное описание: Вместо исходного многомерного описания данных, которое часто бывает избыточным, метод генерирует компактное информативное описание данных, которое легче обрабатывать последующим алгоритмам. При этом, настраивая число используемых компонент $K$, можно эффективно управлять степенью переобучения модели: уменьшение $K$ снижает эффективную сложность модели, ограничивая её способность «подстраиваться» под шум в данных.

Предварительная подготовка признаков

Перед применением метода главных компонент крайне важно выполнить стандартизацию (standardization) признаков, включающую центрирование и приведение признаков признаков к одному масштабу.

Это важно по следующим причинам:

• Если не провести центрирование (вычитание глобального среднего значения из каждого объекта), первая главная компонента может указать не на направление максимального разброса, а на вектор, направленный из начала координат к центру облака точек. Тогда алгоритм не будет описывать внутреннюю структуру данных.

• Если один признак $\boldsymbol{x}^1$ измеряется в миллионах, а другой $\boldsymbol{x}^2$ — в долях единицы, метод ошибочно решит, что направление первого признака содержит всю информацию просто из-за разницы в масштабе.

Вычислительная сложность

Алгоритм состоит из трёх основных этапов: центрирование признаков, расчёт ковариационной матрицы и поиск её собственных векторов.

Сложность нахождения всех собственные векторы и собственных чисел матрицы размера $D \times D$ равна $O(D^3)$.

На практике нас чаще всего интересует не полное разложение, нахождение только первых $K$ главных компонент. В этом случае их можно вычислить с использованием степенного метода (power method) за $O(K D^2)$.

Также часто главные компоненты находят из сингулярного разложения (Singular Value Decomposition, SVD) матрицы данных $X$.

Оценка числа главных компонент

Для оценки информативности выбранных направлений и определения оптимального количества новых признаков используют два ключевых показателя: индивидуальную и накопленную доли объяснённой дисперсии.

Доля объяснённой дисперсии

Доля объяснённой дисперсии (Explained Variance Ratio, EVR) для конкретной $k$-й компоненты показывает, какую часть суммарного разброса данных описывает именно это направление:

$$EVR_k = \frac{\lambda_k}{\sum_{j=1}^D \lambda_j}$$

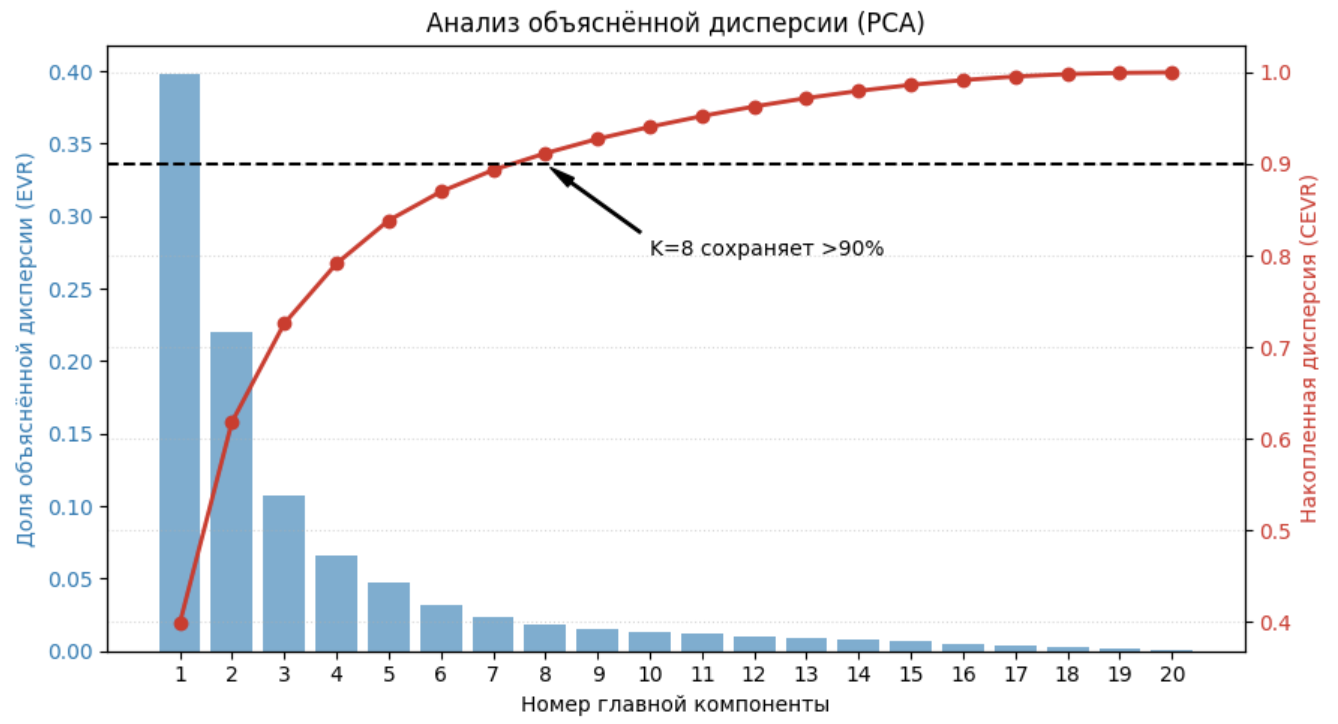
На практике строят график зависимости доли объяснённой дисперсии от номера компоненты, по которому подбирают, какое число главных компонент использовать. Обычно первые компоненты имеют высокое значение показателяЮ в отличие от последующих, и только их оставляют для дальнейшего анализа.

Накопленная доля объяснённой дисперсии

Накопленная доля объяснённой дисперсии (Cumulative Explained Variance Ratio, CEVR) характеризует суммарную информативность первых $K$ выбранных главных компонент:

$$CEVR_K = \frac{\sum_{i=1}^K \lambda_i}{\sum_{j=1}^D \lambda_j}$$

Данная величина монотонно возрастает с увеличением $K$ и достигает 1 (или 100%), когда число компонент становится равным исходной размерности признакового пространства $D$.

Эта величина также используется для подбора числа главных компонент: задают порог (90%, 95% или 99%), а далее выбирают минимальное число первых $K$ главных компонент, которые сохраняют заданную долю объяснённой дисперсии.

В последующих главах будут

• аналитически выведены главные компоненты;

• доказаны свойства проекций на главные компоненты;

• показана глобальная оптимальность первых $K$ главных компонент.

Поскольку данные описываются конечной выборкой объектов $\boldsymbol{x}_1,\boldsymbol{x}_2,...\boldsymbol{x}_N$, то операции математического ожидания и дисперсии в этих главах следует понимать в конечном пространстве исходов этой выборки, что соответствует операциям выборочного среднего и выборочной дисперсии.