Модель ResNet

Модель ResNet [1] стала победителем соревнования ILSVRC-2015, ансамбль из вариантов которой показал частоту ошибок 3.6%, что ниже, чем оцениваемая частота ошибок человека (5.1% из [2]).

Проблема глубоких сетей

Авторы модели проводили эксперименты по увеличению глубины свёрточной сети и обнаружили, что с некоторого момента добавление новых слоёв приводит к ухудшению качества прогнозов модели не только на тестовой, но и на обучающей выборке!

Это показано ниже для частоты ошибок на обучающей выборке (слева) и тестовой выборке (справа) датасета CIFAR-10 [3] при увеличении глубины сети от 20 до 56 слоёв [1]:

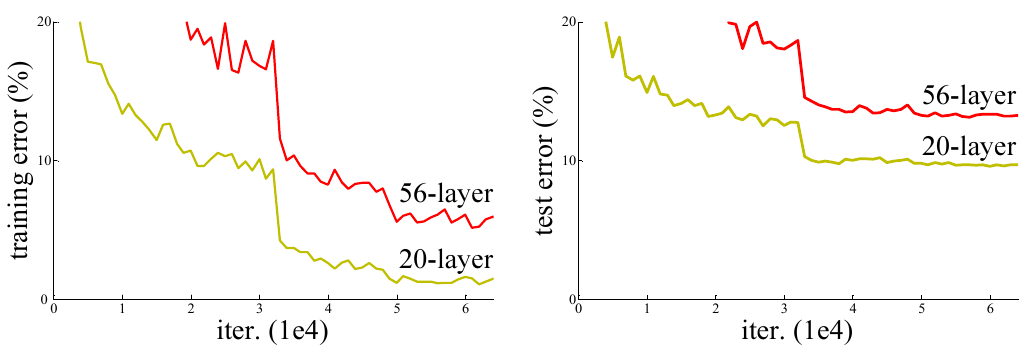
После каждой свёртки использовалась батч-нормализация, нормы градиентов не взрывались и не вырождались. Поэтому авторы пришли к выводу, что падение качества прогнозов вызвано чрезмерным замедлением скорости настройки весов.

Остаточный блок

Как мы увидели, простое наращивание числа слоёв может ухудшить качество модели по сравнению с неглубокой. В то же время легко воспроизвести качество неглубокой сети с помощью глубокой, просто дополнив неглубокую сеть новыми тождественными преобразованиями, не изменяющими входы. Это дало понимание того, что глубокой сети сложно воспроизвести тождественное преобразование. Чтобы ей посодействовать в этом, было предложено использовать остаточный блок (residual block), представленный ниже [1]:

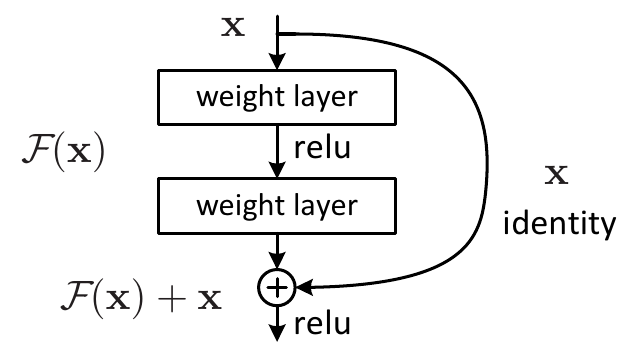
Результатом действия остаточного блока является сумма нелинейного преобразования и исходного входа $\mathcal{F}(\mathbf{x})+\mathbf{x}$. Такой конструкции гораздо проще воспроизвести тождественное преобразование, для чего достаточно задать нулями все веса преобразования $\mathcal{F}(\mathbf{x})$, превратив его в тождественный ноль.

Заключительный слой $\mathcal{F}(\mathbf{x})$ не содежит нелинейности ReLU. Вместо этого нелинейность ставится после выхода ResNet-блока. Это сделано для того, чтобы преобразование $\mathcal{F}(\mathbf{x})$ могло как повысить, так и понизить значение входа $\mathbf{x}$.

Эксперименты показали, что если наращивать сеть, добавляя в неё остаточные блоки, то точность прогнозов растёт, а не падает, как в обычной свёрточной архитектуре. Эта несложная идея сделало возможным применение очень глубоких сетей, содержащих 100 слоёв и более, а работа [1] стала одной из самых цитируемых в области глубокого обучения!

Архитектура ResNet

Для суммирования преобразования $\mathcal{F}(\mathbf{x})$ и входа $\mathbf{x}$ необходимо, чтобы число каналов и пространственные размеры в результате преобразования не изменялись. Поэтому в $\mathcal{F}(\mathbf{x})$ использовались свёртки 3x3 с шагом 1 и паддингом, равным единице.

Периодически пространственное разрешение уменьшалось в два раза, что реализовывалось свёрткой с шагом 2 в преобразовании $\mathcal{F}(\mathbf{x})$, а в тождественной связи применялась свёртка 1x1 также с шагом 2.

Ниже приведена архитектура VGG-19 (слева), её расширенная версия с большим числом слоёв (в центре) и она же, но с добавлением тождественных связей (справа) [1]:

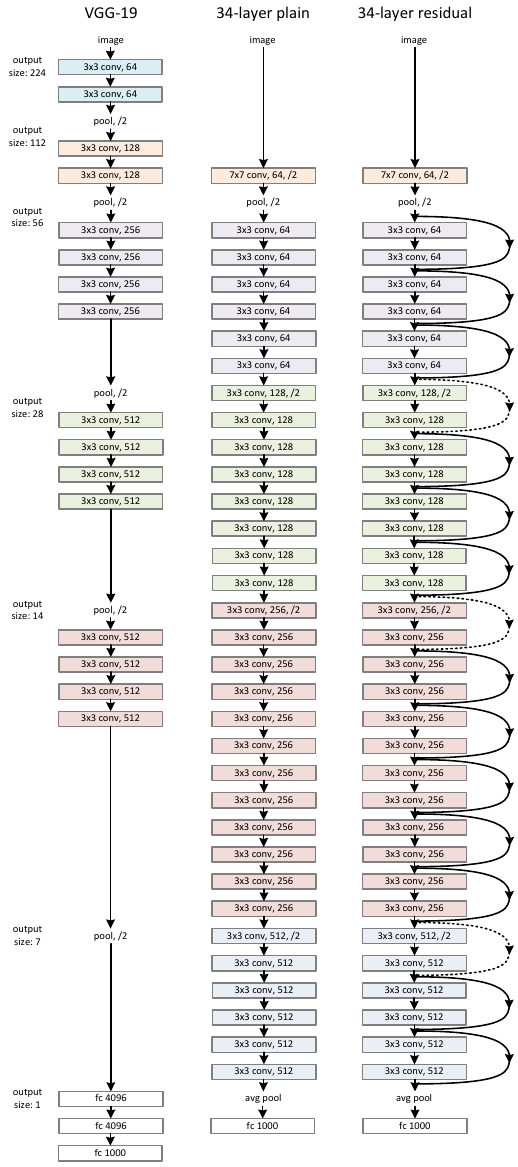
На рисунке обычные тождественные связи показаны сплошной линией, а тождественные связи, на которых пространственное разрешение уменьшается в 2 раза, - пунктиром.

После работы всех остаточных блоков их результат векторизуется глобальным усредняющим пулингом, к которому применяется всего один полносвязный слой.

Такая архитектура, несмотря на большее число слоёв, имеет гораздо меньше настраиваемых параметров, чем относительно неглубокая сеть VGG, использующая несколько полносвязных слоёв.

Варианты архитектуры

Тестировались архитектуры с разным числом слоёв - ResNet-18, ResNet-34, ResNet-50, ResNet-101, ResNet-152. Среди них самой точной оказалась архитектура с 152 слоями (частота ошибок 4.5% на датасете ImageNet):

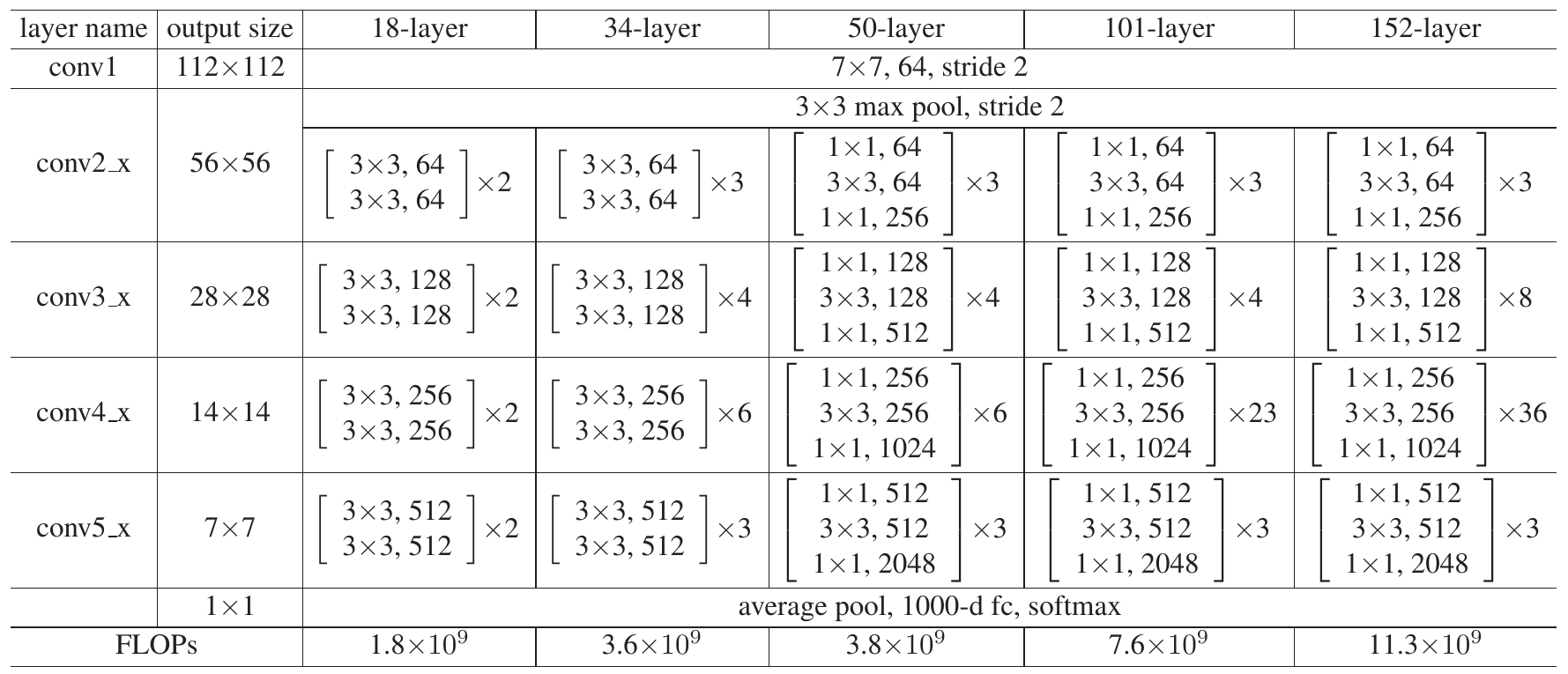
Нелинейные преобразования $\mathcal{F}(\mathbf{x})$ различались для числа слоёв 34,50 и 101,152. В первом случае они реализовывались двумя свёртками с пространственными размерами (размером ядра) 3x3, а во втором - тремя свёртками 1x1, 3x3, 1x1. Первая 1x1 свёртка уменьшала число каналов, снижая число параметров и количество операций второй свёртки 3x3, а третья - восстанавливала исходное число каналов. За счёт этого приёма число операций (нижняя строка таблицы) и параметров оказалось сравнимым для более и менее глубоких вариантов ResNet.

Этот приём называется "бутылочным горлышком" (bottleneck), с которым мы уже сталкивались в модели GoogLeNet.

подсказка

Изменение размерности в нелинейном преобразовании $\mathcal{F}(\mathbf{x})$

Если в нелинейном преобразовании изменяется число каналов, то его можно синхронно изменить в тождественной ветке, добавив в неё свёрточный слой из свёрток 1x1. Если же изменяется пространственная размерность, то в тождественную связь можно включить соответствующее перемасштабирование входа $\mathbf{x}$.

Преимущества ResNet

• Тождественные связи позволяют градиенту лучше распространяться назад при обучении модели, ускоряя настройку более ранних слоёв нейросети.

• Тождественные связи упрощают начальную инициализацию глубокой сети: веса нелинейных преобразований нужно инициализировать значениями, близкими к нулю, чтобы в начале оптимизации $\mathcal{F}(\mathbf{x})\approx 0$. Если оптимизатор сети сочтёт, что сети не хватает выразительной способности для обработки сложных объектов, он настроит $\mathcal{F}(\mathbf{x})$ нужным образом, причём только для тех блоков, которые действительно необходимы.

• ResNet позволяет одновременно обрабатывать как сложные объекты, так и простые. Для распознавания первых нужно много слоёв, а для вторых - мало. В последнем случае признаки извлекаются из сигнала, который прошёл через небольшое число нелинейных преобразований, а дальше распространялся в основном по тождественным связям.

• ResNet действует как ансамбль, поскольку каждый входной сигнал обрабатывается не по одной ветке обработки, а сразу по набору альтернативных веток, причем число альтернатив растёт экспоненциально с увеличением числа остаточных блоков. Это проиллюстрировано для трёх блоков в [4]:

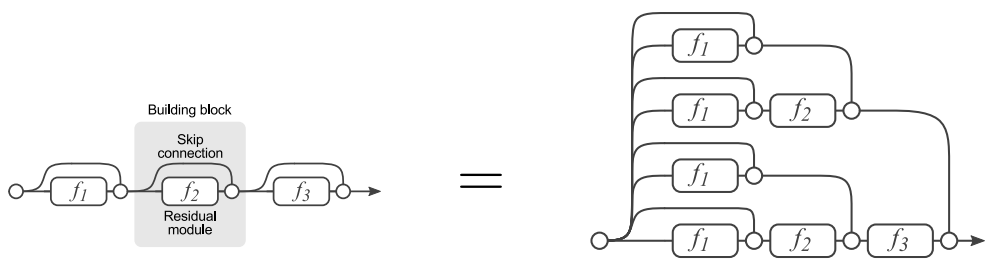
Литература

1. He K. et al. Deep residual learning for image recognition //Proceedings of the IEEE conference on computer vision and pattern recognition. – 2016. – С. 770-778.
2. Russakovsky O. et al. Imagenet large scale visual recognition challenge //International journal of computer vision. – 2015. – Т. 115. – С. 211-252.
3. CIFAR-10 dataset.
4. Veit A., Wilber M. J., Belongie S. Residual networks behave like ensembles of relatively shallow networks //Advances in neural information processing systems. – 2016. – Т. 29.