Пулинг для изображений

Локальный пулинг

Операция пулинга (pooling), как и для случая последовательностей, призвана уменьшить пространственную размерность выхода за счёт разбиения карты признаков (feature map) на фрагменты и применения агрегирующей операции к каждому фрагменту.

Чаще всего используются:

• максимизирующий пулинг (max pooling, агрегирующая операция - взятие максимума);

• усредняющий пулинг (average pooling, агрегирующая операция - усреднение).

Пример применения этих видов пулинга 2x2 приведён ниже для одного канала:

Пулинг применяется к каждому каналу независимо. Например, при его применении к RGB-изображению, он применяется независимо к R-,G- и B-каналу. У стандартных пулингов, приведённых выше, нет настраиваемых параметров, а гиперпараметрами выступает размер агрегируемой области (kernel size) и шаг (stride), причём шаг обычно выбирается равным стороне квадрата, по которому производится агрегация, то есть каждый раз агрегация производится по непересекающимся фрагментам, как на рисунке выше.

Как и в случае последовательностей и временных рядов, пулинг обеспечивает приближённую инвариантность к небольшим сдвигам.

Максимизирующий пулинг извлекает характеристику того, что исходный признак присутствует где-либо в области, по которой производилась агрегация. А усредняющий пулинг извлекает среднюю представленность признака в области.

Комбинация пулингов

В [1] предлагается возвращать в качестве результата взвешенное среднее от максимизирующего и усредняющего пулингов:

$$\mathbf{y}=a\cdot max(\mathbf{x})+(1-a)\cdot avg(\mathbf{x})$$

где $a$ - настраиваемый параметр либо функция, зависящая от обрабатываемого входа $\sigma(\mathbf{w}^T \mathbf{x})$.

Глобальный пулинг

Так же, как и для случая временных рядов, можно применять глобальную агрегацию (global pooling [2]) по всем пространственным координатам. Если на входе было $C$ каналов, то на выходе получим $C$-мерный вектор, состоящий из агрегированных значений каналов по всем пространственным координатам, как показано ниже:

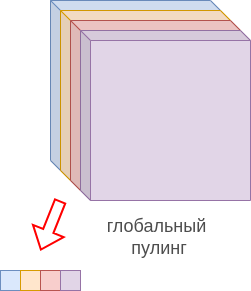
Это полезно, чтобы перевести изображение произвольного пространственного размера в вектор фиксированной размерности (эмбеддинг) перед его обработкой многослойным персептроном (например, для классификации изображений).

Интерпретируемость

Если число каналов совпадает с числом классов, то результат глобального пулинга можно трактовать как рейтинги предсказываемых классов, SoftMax-преобразование от которых приведёт к вероятностям классов. Этот подход обладает повышенной интерпретируемостью, поскольку, визуализируя канал, соответствующий каждому из классов, можно понять, какие области изображения голосуют за тот или иной класс, обладая максимальными значениями в областях карты признаков, к которой применяется глобальный пулинг.

Пирамидальный пулинг

Глобальный пулинг, агрегируя по всем пространственным координатам, теряет всю пространственную информацию. Если необходимо представить изображение в виде вектора фиксированного размера, сохранив хотя бы часть пространственной информации, то рекомендуется использовать пирамидальный пулинг (spatial pyramid pooling, [3]), как мы уже показывали при обработке последовательностей.

В этом виде пулинга в качестве гиперпараметров задаётся набор сеток фиксированного размера, например, 1x1 и 4x4, затем карта признаков изображения разбивается этими сетками на области, после чего к каждой области применяется глобальный пулинг (усредняющий или максимизирующий), а результаты этих пулингов объединяются (конкатенируются), как показано на рисунке:

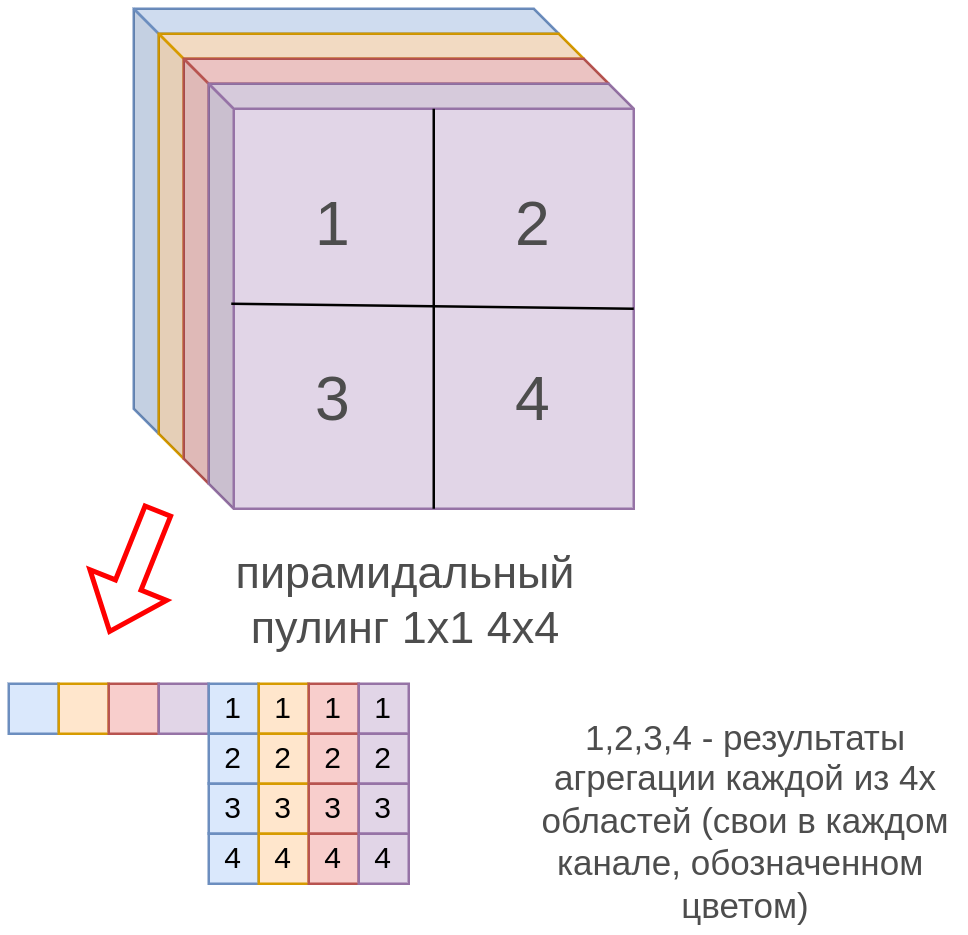
Например, в пирамидальном максимизирующем пулинге для четырёхканального представления изображения его выходом будут максимальные значения для каждого канала целиком, а также максимальные значения в рамках каждой области 1,2,3,4 для каждого канала, то есть вектор из 4+4*4=20 значений.

Пирамидальный пулинг также переводит изображение произвольного размера в вектор фиксированной размерности, но теперь пространственная информация частично сохранена, поскольку теперь известно, в какой области был достигнут каждый из максимумов.

В пирамидальный пулинг часто добавляют более мелкие сетки, такие как 8x8 и 16x16.

Литература

1. Lee C. Y., Gallagher P. W., Tu Z. Generalizing pooling functions in convolutional neural networks: Mixed, gated, and tree //Artificial intelligence and statistics. – PMLR, 2016. – С. 464-472.
2. Lin M., Chen Q., Yan S. Network in network //arXiv preprint arXiv:1312.4400. – 2013.
3. He K. et al. Spatial pyramid pooling in deep convolutional networks for visual recognition //IEEE transactions on pattern analysis and machine intelligence. – 2015. – Т. 37. – №. 9. – С. 1904-1916.