Нормализация слоя

Другим способом нормализации активаций сети для упрощения её настройки является нормализация слоя (layer normalization, [1]), сокращенно называемый LayerNorm.

Слой LayerNorm принимает на вход активации $z_1,...z_M$ предыдущего слоя и их линейно перемасштабирует:

$$\begin{align*} & z_1 \;&\to\quad &\gamma_1\frac{z_1-\mu}{\sqrt{\sigma^2+\delta}}+\beta_1 \\ & z_2 \;&\to\quad &\gamma_2\frac{z_2-\mu}{\sqrt{\sigma^2+\delta}}+\beta_2 \\ & \cdots & \cdots \\ & z_M \;&\to\quad &\gamma_M\frac{z_M-\mu}{\sqrt{\sigma^2+\delta}}+\beta_M \\ \end{align*}$$

где $\delta>0$ - малая константа, призванная исключить деление на ноль, а параметры $\mu$ и $\sigma$ вычисляются как выборочное среднее и стандартное отклонение по активациям всех нейронов слоя в рамках одного объекта:

$$\begin{align*} \mu &= \frac{1}{M}\sum_{m=1}^M z_m \\ \sigma &= \sqrt{\frac{1}{M}\sum_{m=1}^M (z_m-\mu)^2} \\ \end{align*}$$

Параметры $\{\beta_i\}_i$ и $\{\gamma_i\}_i$ настраиваются вместе с остальными весами нейросети.

Схематично работа LayerNorm представлена ниже:

Преимущество по сравнению с батч-нормализацией

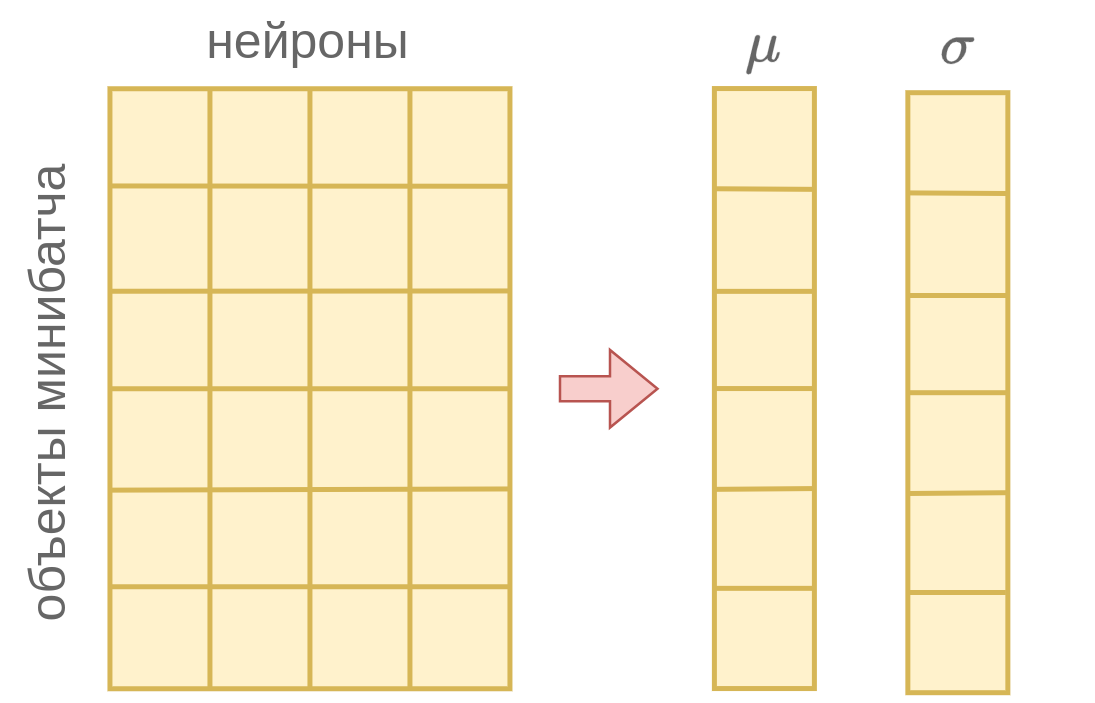
Поскольку усреднение для расчёта $\mu$ и $\sigma$ производится по активациям нейронов слоя в рамках одного объекта, то метод работает одинаково в режиме обучения и применения, что повышает обобщаемость настроенной модели на новые данные. Также нейросеть можно настраивать с любым размером мини-батча, даже по отдельным объектам.

Нормализация слоя была предложена для ускорения и повышения стабильности настройки рекуррентных нейросетей, а сейчас активно используется в архитектуре нейросетей-трансформетров.

Литература

1. Ba J. L., Kiros J. R., Hinton G. E. Layer normalization //arXiv preprint arXiv:1607.06450. – 2016.