Батч-нормализация

Идея метода

Классическим подходом к повышению качества прогнозов моделей является нормализация признаков, то есть приведение признаков к одинаковой шкале поскольку это выравнивает способность разных признаков влиять на прогноз.

Самым популярным методом нормализации является стандартизация (standardization), приводящая каждый признак $x^i$ со средним $\mu_i$ и стандартным отклонением $\sigma_i$ к его стандартизованной версии со средним ноль и единичной дисперсией:

x^i \longrightarrow \frac{x^i-\mu_i}{\sigma_i}

Нормализация также ускоряет настройку градиентными методами [1], поскольку делает линии уровня функции потерь менее вытянутыми и более скруглёнными, как показано на рисунке:

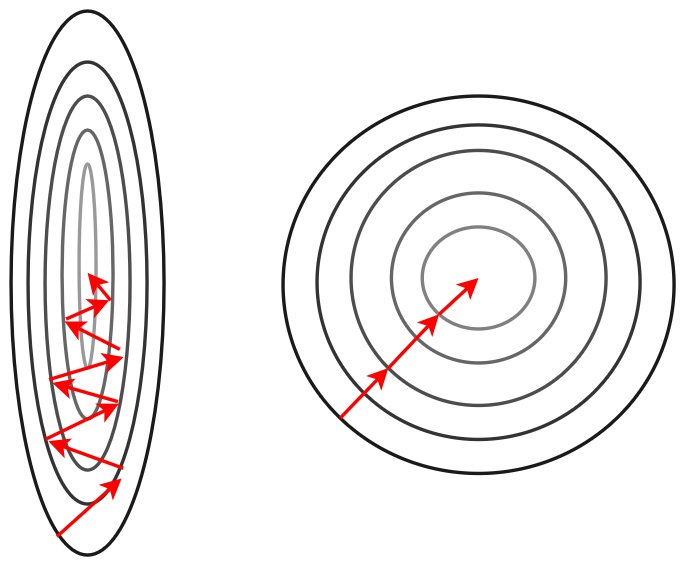
Батч-нормализация (batch-normalization, [1]) позволяет ускорить настройку сети за счёт нормализации не только входных признаков, но и активаций промежуточного слоя.

Слой батч-нормализации принимает на вход активации $z_1,...z_M$ предыдущего слоя и их линейно перемасштабирует таким образом, чтобы они имели средние $\beta_1,...\beta_M$ и стандартные отклонения $\gamma_1,...\gamma_M$ :

\begin{aligned} & z_1 \;&\to\quad &\gamma_1\frac{z_1-\mu_1}{\sqrt{\sigma_1^2+\delta}}+\beta_1 \\ & z_2 \;&\to\quad &\gamma_2\frac{z_2-\mu_2}{\sqrt{\sigma_2^2+\delta}}+\beta_2 \\ & \cdots & \cdots \\ & z_M \;&\to\quad &\gamma_M\frac{z_M-\mu_M}{\sqrt{\sigma_M^2+\delta}}+\beta_M \\ \end{aligned}

где

$\mu_1,...\mu_M$ - средние значения активаций $z_1,...z_M$ ;
$\sigma_1,...\sigma_M$ - стандартные отклонения активаций $z_1,...z_M$ ;
$\delta>0$ - малая константа, призванная исключить деление на ноль.

Слой батч-нормализации (batch-normalization layer), нормирующий активации предыдущего слоя, может включаться в любом месте сети.

Его используют многократно для более ранних и более поздних слоёв.

Параметры $\{\beta_i\}_i$ и $\{\gamma_i\}_i$ настраиваются вместе с остальными весами нейросети. Если для минимизации потерь действительно необходима стандартизация, то они настроятся на значения 0 и 1 соответственно. Если же стандартизация не нужна, то они настроятся на значения средних $\{\mu_i\}_i$ и стандартных отклонений $\{\sigma_i\}_i$ соответственно, и слой батч-нормализации будет действовать как тождественное преобразование. В общем же случае эти параметры будут принимать некоторые промежуточные значения.

Удаление лишних параметров

В линейном слое, применяемом к батч-нормализованным входам, необязательно использовать смещения (bias), поскольку нейроны уже смещаются на выучиваемые смещения $\{\beta_i\}_i$ из батч-нормализации.

Батч-нормализация будет по-разному действовать при обучении и применении нейросети. Рассмотрим эти различия.

Обучение нейросети

Если при стандартизации признаков мы могли предварительно вычислить их средние и стандартные отклонения, то для активаций промежуточных нейронов - уже нет, поскольку при настройке сети веса меняются, что изменяет распределение всех последующих нейронов!

Поэтому во время обучения сети (training) на каждом шаге обновления весов $\{\mu_i\}_i$ и $\{\sigma_i\}_i$ перевычисляются как выборочные средние и стандартные отклонения нейронов по текущему мини-батчу, как показано ниже:

Точность оценки

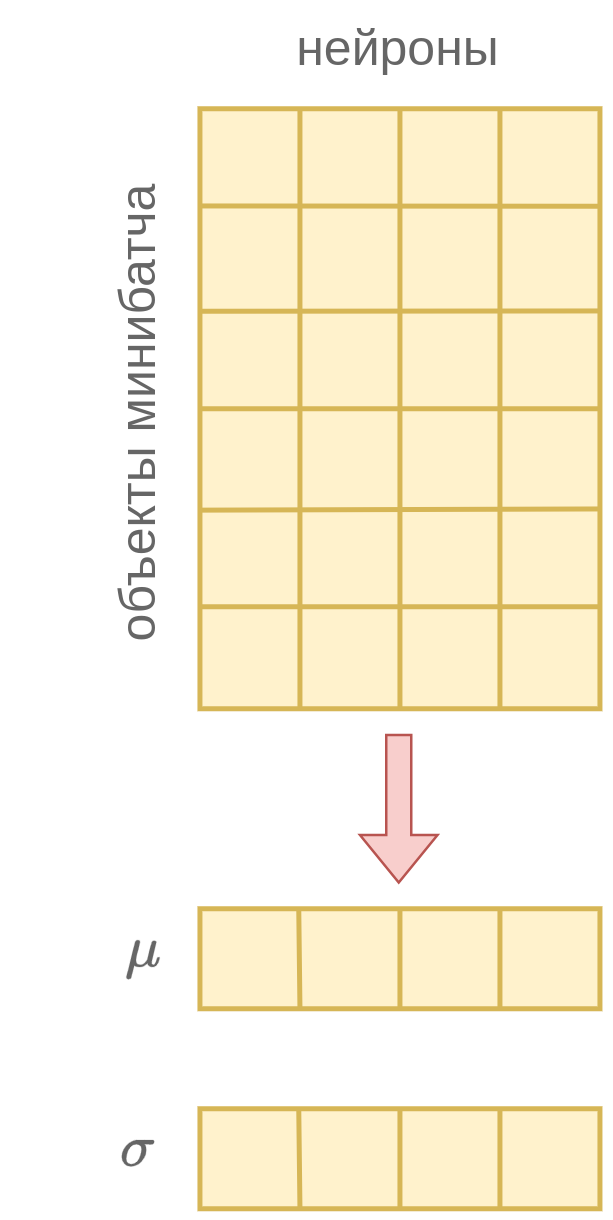
Для повышения точности оценки средних и стандартных отклонений (и, как следствие, повышения устойчивости батч-нормализации) рекомендуется настраивать нейросеть с повышенным размером мини-батчей.

Применение нейросети

Во время применения (inference) уже обученной сети мы уже могли бы вычислить средние и стандартные отклонения нейронов, поскольку веса сети уже настроены и зафиксированы, следовательно распределения промежуточных активаций зафиксированы и не меняются. Однако это предполагает дополнительный проход по обучающей выборке. На практике, чтобы его не делать, во время обучения вычисляются не только средние и стандартные отклонения по текущему мини-батчу, но и их сглаженные версии, используя экспоненциальное сглаживание. В результате к концу обучения мы просто подставляем вместо $\{\mu_i\}_i$ и $\{\sigma_i\}_i$ их сглаженные значения.

Обоснование метода

Если поместить батч-нормализацию перед функцией нелинейности, то при соответствующей инициализации параметров $\gamma$ и $\beta$ она будет приводить аргумент нелинейности в регион её существенных изменений (изгиб в функциях ReLU, LeakyReLU, tangh и т.д.).

Также батч-нормализация ускоряет настройку сети в целом за счёт ускорения настройки её более поздних слоёв. Как мы знаем, на каждой итерации оптимизации все веса сети обновляются одновременно. Но в контексте обновлённых весов более ранних слоёв распределение активаций более поздних слоёв поменялось, и обновления весов для поздних слоёв перестаёт быть актуальным! В итоге настройка сети замедляется, поскольку оптимизатору необходимо вначале настроить более ранние слои, и, когда они уже почти перестанут меняться, осуществлять предметную настройку зависящих от них более поздних слоёв.

Батч-нормализация упрощает и ускоряет одновременную настройку более ранних и более поздних слоёв за счёт того, что выходы слоя батч-нормализации, являющиеся входами последующего слоя, будут иметь предсказуемые средние и стандартные отклонения. Соответственно, слою, который эти выходы использует, будет проще под них настроить веса.