Перейти к основному содержимому

Обрезка градиента

Неустойчивость оптимизации​

Нейросети моделируют сложные нелинейные зависимости, вследствие чего рельеф функции потерь может быть сложным и подверженным резким изменениям, что может приводить к неустойчивой оптимизации весов как показано на рисунке [1]:

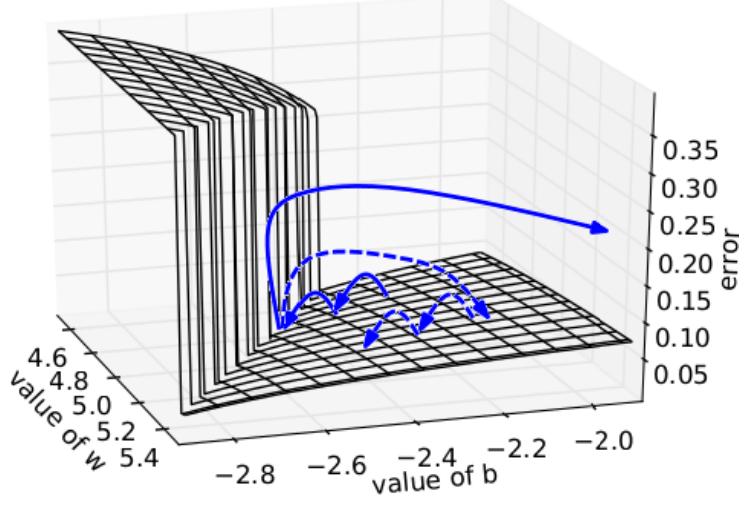
Для стабилизации обучения приходится снижать шаг обучения, замедляя его. Хотелось бы уменьшать сдвиг не постоянно, а только в областях резкого изменения функции, что достигается методом обрезки градиента.

Обрезка градиента​

Обрезка градиента (gradient clipping, [1]) - популярная процедура, повышающая стабильность и скорость обучения нейросетей. Поскольку при изменчивом ландшафте функции потерь могут возникать большие по норме градиенты, то перед каждым обновлением весов в методе стохастического градиентного спуска норма градиента сравнивается с некоторым порогом λ>0\lambda>0. Если норма меньше порога, то веса обновляются как обычно, а если больше - то норма градиента обрезается порогом λ\lambda перед обновлением весов:

w→{w−ε∇wL(y^i,yi),если ∥∇wL(y^i,yi)∥<λw−ελ∇wL(y^i,yi)∥∇wL(y^i,yi)∥,если ∥∇wL(y^i,yi)∥≥λ\mathbf{w}\to\begin{cases} \mathbf{w}-\varepsilon\nabla_{\mathbf{w}}\mathcal{L}(\widehat{y}_{i},y_{i}), & \text{если }\left\lVert \nabla_{\mathbf{w}}\mathcal{L}(\widehat{y}_{i},y_{i})\right\rVert <\lambda\\ \mathbf{w}-\varepsilon\lambda\frac{\nabla_{\mathbf{w}}\mathcal{L}(\widehat{y}_{i},y_{i})}{\left\lVert \nabla_{\mathbf{w}}\mathcal{L}(\widehat{y}_{i},y_{i})\right\rVert }, & \text{если }\left\lVert \nabla_{\mathbf{w}}\mathcal{L}(\widehat{y}_{i},y_{i})\right\rVert \ge\lambda \end{cases}

Этот приём позволил существенно повысить стабильность и скорость настройки рекуррентных нейронных сетей, в которых из-за многократно повторяемых слоёв с одинаковыми весами проблема нестабильных градиентов стоит особенно остро.

Адаптивная обрезка градиента​

Также можно использовать адаптивную обрезку градиента (adaptive gradient clipping, [2]):

w→{w−ε∇wL(y^i,yi),если ∥∇wL(y^i,yi)∥/∥w∥<λw−ελ∥w∥∇wL(y^i,yi)∥∇wL(y^i,yi)∥,если ∥∇wL(y^i,yi)∥/∥w∥≥λ\mathbf{w}\to\begin{cases} \mathbf{w}-\varepsilon\nabla_{\mathbf{w}}\mathcal{L}(\widehat{y}_{i}, y_{i}), & \text{если }\left\lVert \nabla_{\mathbf{w}}\mathcal{L}(\widehat{y}_{i},y_{i})\right\rVert /\left\Vert \mathbf{w}\right\Vert <\lambda\\ \mathbf{w}-\varepsilon\lambda\left\Vert \mathbf{w}\right\Vert \frac{\nabla_{\mathbf{w}}\mathcal{L}(\widehat{y}_{i},y_{i})}{\left\lVert \nabla_{\mathbf{w}}\mathcal{L}(\mathbf{\widehat{y}_{i}},y_{i})\right\rVert }, & \text{если }\left\lVert \nabla_{\mathbf{w}}\mathcal{L}(\widehat{y}_{i},y_{i})\right\rVert /\left\Vert \mathbf{w}\right\Vert \ge\lambda \end{cases}

В этом случае гораздо проще и интуитивнее задать порог λ\lambda, который теперь соответствует не максимальному абсолютному изменению весов, а их максимальному относительному изменению.

Например, мы можем задать ограничение, что на каждой итерации оптимизации веса не должны меняться больше, чем на 10% от их нормы.

Проблемой остаётся необходимость выбора единого порога λ\lambda, который не будет оптимальным для всех весов, поскольку часть из них изменяются в широком диапазоне значений, а другая часть - в узком. Поэтому лучше работает адаптивное ограничение градиента для каждого веса wiw_i (и его градиента) в отдельности:

wi→{wi−ε∇wiL(y^i,yi),если ∣∇wiL(y^i,yi)∣/∣wi∣∗<λwi−ελ∣wi∣∗∇wiL(y^i,yi)∣∇wiL(y^i,yi)∣,если ∣∇wiL(y^i,yi)∣/∣wi∣∗≥λw_{i}\to\begin{cases} w_{i}-\varepsilon\nabla_{w_{i}}\mathcal{L}(\widehat{y}_{i},y_{i}), & \text{если }\left| \nabla_{w_{i}}\mathcal{L}(\widehat{y}_{i},y_{i})\right| /\left| w_{i}\right| ^{*}<\lambda\\ w_{i}-\varepsilon\lambda\left| w_{i}\right| ^{*}\frac{\nabla_{w_{i}}\mathcal{L}(\widehat{y}_{i},y_{i})}{\left| \nabla_{w_{i}}\mathcal{L}(\widehat{y}_{i},y_{i})\right| }, & \text{если }\left| \nabla_{w_{i}}\mathcal{L}(\widehat{y}_{i},y_{i})\right| /\left| w_{i}\right| ^{*}\ge\lambda \end{cases}

В формуле ∣wi∣∗=max⁡(∣wi∣,ν)\left| w_{i}\right| ^{*}=\max\left(\left| w_{i}\right| ,\nu\right) , а ν=10−3\nu=10^{-3} - гиперпараметр для исключения деления на ноль.

В работе [2] замена батч-нормализации адаптивным ограничением градиента позволила обучить сеть ResNet быстрее и повысить качество её прогнозов.

Литература​

  1. Pascanu R., Mikolov T., Bengio Y. On the difficulty of training recurrent neural networks //International conference on machine learning. – Pmlr, 2013. – С. 1310-1318.
  2. Brock A. et al. High-performance large-scale image recognition without normalization //International conference on machine learning. – PMLR, 2021. – С. 1059-1071.