Контроль качества предсказания вероятностей

Калибровка вероятностей

Во многих задачах классификации важно не только уметь предсказывать метки классов, но и их вероятности. Например:

• При обнаружении неправомерных злонамеренных действий в сети важно оценивать их вероятность, чтобы балансировать между ложными срабатываниями и пропущенными инцидентами.

• При медицинской диагностике важно оценивать вероятность болезни по снимкам/анализам, чтобы принимать решение о дальнейшей диагностике.

Подбор преобразования $F_{\tau}(g)$ и его параметров $\tau$, переводящего рейтинг класса $g$ в его вероятность, называется калибровкой вероятностей (probability calibaration).

График калибровки

Для контроля качества калибровки бинарной классификации строят график калибровки (calibration-plot), показанный ниже [1]:

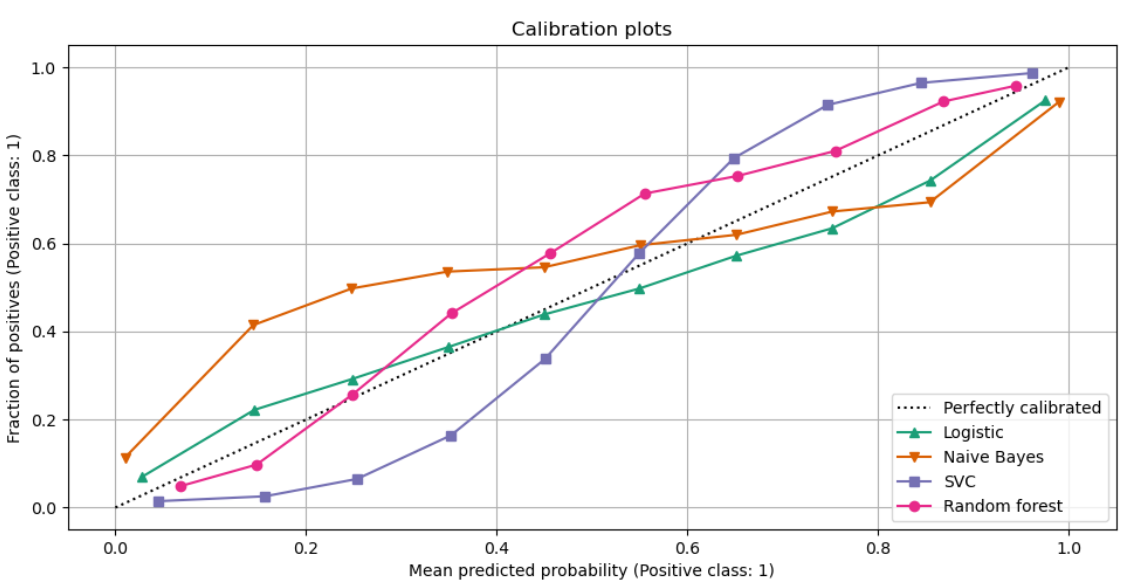
По оси X откладывают предсказанную вероятность положительного класса, а по оси Y - фактическую. Чем получаемая зависимость ближе к диагонали Y=X, тем лучше классификатор предсказывает вероятности.

Например, на графике выше видно, что метод Naive Bayes недооценивает истинную вероятность, когда предсказывает её малое значение, и, наоборот, переоценивает вероятность, когда предсказывает её большое значение.

Поскольку в обучающей выборке нам даны только истинные классы, а не их вероятности, то для расчета истинных вероятностей множество предсказанных вероятностей разбивают на отрезки, например:

$$\hat{p}(y=+1|\mathbf{x})\le 0.1,\quad 0.1<\hat{p}(y=+1|\mathbf{x})\le 0.2,\quad ...\quad 0.9<\hat{p}(y=+1|\mathbf{x})$$

В рамках каждого отрезка вычисляют фактическую вероятность положительного класса как долю объектов, принадлежащих этому классу.

Качество прогнозов меток и вероятностей классов

Подчеркнём, что даже если классификатор хорошо предсказывает метки классов, вероятности классов он может предсказывать плохо, как, например, на рисунке ниже:

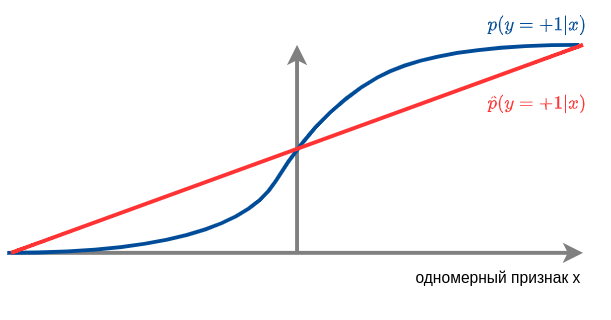
Классификатор верно настроился на то, что:

• При $x<0$ вероятность положительного класса меньше 0.5, и надо предсказывать отрицательный класс.

• При $x>0$ положительный класс более вероятен, и нужно предсказывать его.

Поэтому точность предсказания меток класса будет высокой, однако вероятности классов предсказываются неверно, поскольку $\hat{p}(y=+1|x)\ne p(y=+1|x)$!

Базовые меры качества классификации, такие как accuracy, error rate, precision, recall и др., оценивают только качество предсказания меток классов.

Для оценки качества предсказания вероятностей можно использовать среднее значение логарифма правдоподобия или оценку Бриера. Эти меры будут описаны ниже.

Переобучение

Во избежание переобучения необходимо, как и для других мер качества, проводить оценку на внешней выборке, а не на обучающей (по которой настраивались параметры) и валидационной (по которой настраивались гиперпараметры)!

Средний логарифм правдоподобия

Наша вероятностная модель $f_\mathbf{w}(\mathbf{x})$ сопоставляет каждому наблюдению $(\mathbf{x},y)$ вероятность пронаблюдать именно такой класс $\hat{p}_\mathbf{w}(y|\mathbf{x})$. При предположении, что объекты выборки распределены независимо, вероятность пронаблюдать ответы на всей выборке $(X,Y)$ факторизуется в произведение вероятностей пронаблюдать ответ на каждом объекте выборки:

$$\hat{p}_\mathbf{w}(Y|X)=\prod_{n=1}^N \hat{p}_\mathbf{w}(y|\mathbf{x})$$

Чем выше правдоподобие [2], тем больше прогнозы модели согласуются с фактическими наблюдениями, и тем лучше модель прогнозирует вероятности классов. Поскольку произведение большого числа вероятностей будет вырождаться в машинный ноль из-за ограничения точности переменных с плавающей запятой, то на практике анализируют средний логарифм правдоподобия (log-likelihood):

$$\frac{1}{N}\sum_{n=1}^N \log \hat{p}_\mathbf{w}(y|\mathbf{x})$$

Оценка Бриера

Оценка Бриера представляет собой другой популярный способ оценки качества предсказанных вероятностей с помощью функции потерь Бриера (Brier score [3]), равной среднему квадрату отклонений вектора предсказанных вероятностей от вектора истинных вероятностей по L2-норме.

Пусть $\hat{\mathbf{p}}(y|\mathbf{x})\in\mathbb{R}^C$ - вектор предсказанных моделью вероятностей, а $\mathbf{p}(y|\mathbf{x})\in\mathbb{R}^C$ - вектор истинных вероятностей.

Например, если для объекта $\mathbf{x}$ реализуется $i$-й класс, то $\mathbf{p}(y|\mathbf{x})$ будет представлять собой вектор из нулей, в котором на $i$-й позиции стоит единица.

Тогда оценка Бриера вычисляется по формуле:

$$\text{Brier Score} = \frac{1}{N}\sum_{n=1}^N \|\hat{\mathbf{p}}(y_n|\mathbf{x}_n)-\mathbf{p}(y_n|\mathbf{x}_n)\|_2^2$$

Вопрос

Правдоподобие выборки, логарифм правдоподобия и оценка Бриера измеряют степень ошибки (чем больше, тем хуже) или качество прогноза вероятностей (чем больше, тем лучше)?

Для лучшего понимания процесса калибровки вероятностей рекомендуется ознакомиться с демонстрационным кодом [4].

Литература

1. Документация sklearn: probability calibration.

2. Wikipedia: функция_правдоподобия.

3. Wikipedia: Brier score.

4. Kaggle: probability calibration tutorial.