Базовые меры качества многоклассовой классификации

Ранее мы уже рассматривали оценку качества регрессионных прогнозов, когда целевой отклик - вещественное число $y\in\mathbb{R}$. Теперь рассмотрим оценку качества прогнозов в задаче классификации, в которой целевая величина принимает одно из $C$ дискретных величин:

$$y\in\{1,2,...C\}$$

Несмещённая оценка

Напомним, что качество классификации необходимо оценивать не на обучающей, а на отдельной валидационной выборке, иначе мы смещённую оценку качества! Если же валидационная выборка также использовалась для настройки гиперпараметров, то для оценки качества потребуется третья независимая выборка, которая не использовалась ни для настройки параметров, ни для настройки гиперпараметров.

Далее будут приведены различные стандартные меры оценки качества классификации. При этом важно отслеживать их связь с конечными мерами качества определяющими эффективность задачи, решаемой классификационными моделями.

Точность и частота ошибок

Самой простой и популярной мерой качества является точность классификации (accuracy), которая измеряет долю верных предсказаний:

$$\text{accuracy}=\frac{1}{N}\sum_{n=1}^N \mathbb{I}\{\hat{y}(\mathbf{x}_n)=y_n\}$$

Максимизация точности эквивалентна минимизации частоты ошибок (error rate) классификатора, поскольку они связаны следующим соотношением:

$$\begin{align*} \text{error rate} &=\frac{1}{N}\sum_{n=1}^N \mathbb{I}\{\hat{y}(\mathbf{x}_n)\ne y_n\} \\ &=\frac{1}{N}\sum_{n=1}^N (N-\mathbb{I}\{\hat{y}(\mathbf{x}_n)= y_n\}) \\ &=1-\text{accuracy} \end{align*}$$

Матрица ошибок классификации

Точность и частота ошибок дают агрегированную картину по всем классам, по которой мы не можем понять, на каких именно классах модель чаще всего ошибалась.

Для более детального анализа используется матрица ошибок (confusion matrix) $A\in\mathbb{R}^{C\times C}$ , где каждый элемент $a_{ij}$ показывает количество случаев, когда истинный класс был равен $i$, но при этом был предсказан классом $j$.

На диагонали будут находиться корректные классификации, а внедиагональные элементы будут показывать число ошибок разных типов.

Ниже приведён пример этой матрицы для 3-х классов:

	$\hat{y}=1$	$\hat{y}=2$	$\hat{y}=3$
$y=1$	10	3	0
$y=2$	0	20	15
$y=3$	2	5	30

По этой матрице видно, что в целом классификатор хорошо справился с прогнозированием (диагональные элементы относительно большие). А большая часть ошибок классификатора вызвана тем, что объекты 2-го класса он ошибочно классифицирует 3-м классом. Если классов много, то полезно визуализировать матрицу ошибок в виде тепловой карты значений (heatmap), как на примере ниже:

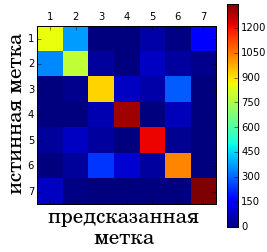
Как по матрице ошибок вычислить точность классификации (accuracy)?

Для расчёта точности нужно просуммировать все диагональные элементы (общее число верных классификаций) и разделить его на сумму всех элементов матрицы (равную общему числу объектов выборки).

Матрица цен

Ошибки классификации различаются тем, какой класс с каким был перепутан. Чаще всего эти ошибки неравноценны между собой.

Например, при классификации электронных писем на "важные", "рассылки" и "спам" не так страшно принять спам за важное письмо и его оставить. Гораздо неприятнее принять важное письмо за спам и его удалить.

Цена ошибки при классификации рассылок меньше, чем при классификации важных писем. Поэтому определяется понятие матрицы ошибок $\Lambda\in\mathbb{R}^{C\times C}$, где каждый элемент $\lambda_{ij}$ показывает штраф за неверную классификацию объекта $i$-го класса $j$-м классом. Диагональные элементы матрицы полагаются равными нулю, поскольку они соответствуют корректным классификациям. Используя матрицу цен, можно вычислять средний штраф (average cost) при классификации всей выборки:

$$\text{average cost} = \frac{1}{N}\sum_{n=1}^N \lambda_{y_n \hat{y}_n} = \frac{1}{N}\sum_{i=1}^C \sum_{j=1}^C a_{ij}\lambda_{ij}$$

При какой матрице цен средний штраф совпадёт с частотой ошибок?

При штрафе равном нулю для верных классификаций и единице для неверных.