Перейти к основному содержимому

Лучший классификатор на ROC кривой

ROC-кривая описывает семейство классификаторов, параметризованных параметром α∈R\alpha\in \mathbb{R}:

y^(x)=sign(g(x)−α)={+1,g(x)≥α−1,g(x)<α\hat{y}(\mathbf{x}) = \text{sign}(g(\mathbf{x})-\alpha) = \begin{cases} +1, & g(\mathbf{x})\ge \alpha \\ -1, & g(\mathbf{x})< \alpha \\ \end{cases}

Но как выбрать лучший экземпляр этого семейства?

В бинарной классификации y∈{+1,−1}y\in\{+1,-1\}, поэтому есть только два типа ошибок:

  • Назначить объекту положительного класса отрицательный класс, что реализуется с вероятностью p(y^=−1∣y=+1)=1−TPRp(\widehat{y}=-1|y=+1)=1-TPR. Обозначим штраф за такую ошибку λ+\lambda_+.

  • Назначить объекту отрицательного класса положительный класс, что реализуется с вероятностью p(y^=+1∣y=−1)=FPRp(\widehat{y}=+1|y=-1)=FPR. Штраф за эту ошибку обозначим λ−\lambda_-.

Тогда средние потери классификатора будут

L=p(y^=−1,y=+1)⋅λ++p(y^=+1,y=−1)⋅λ−=p(y=+1)p(y^=−1∣y=+1)⋅λ++p(y=−1)p(y^=+1∣y=−1)⋅λ−=p(y=+1)(1−TPR)⋅λ++p(y=−1)FPR⋅λ−\begin{aligned} L &= p(\hat{y}=-1,y=+1)\cdot\lambda_+ + p(\hat{y}=+1,y=-1)\cdot\lambda_- \\ &= p(y=+1)p(\widehat{y}=-1|y=+1)\cdot\lambda_{+}+p(y=-1)p(\widehat{y}=+1|y=-1)\cdot\lambda_{-} \\ &= p(y=+1)(1-TPR)\cdot\lambda_{+}+p(y=-1)FPR\cdot\lambda_{-} \end{aligned}

Отсюда в осях FPR,TPRFPR,TPR можно получить изолинии потерь (loss isolines), т.е. множество точек (FPR,TPR), приводящих к одинаковому уровню средних потерь LL:

TPR=1+λ−1p(y=−1)FPR−Lλ+1p(y=+1)TPR=1+\frac{\lambda_{-1}p(y=-1)FPR-L}{\lambda_{+1}p(y=+1)}

Поскольку полученная зависимость TRP(FPR) линейна, то это будет прямая линия с положительным наклоном, а более высоким линиям будут отвечать более низкие ожидаемые потери, как показано на рисунке:

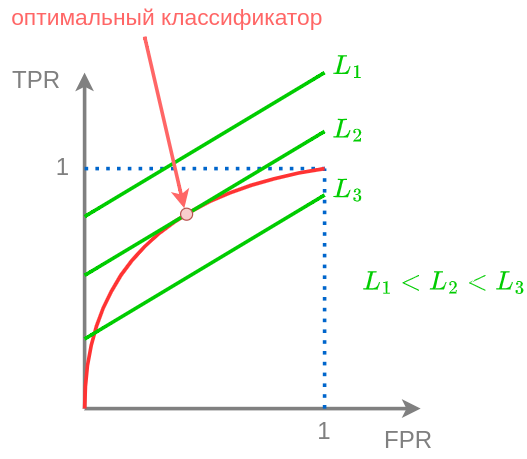
optimal-classifier-on-ROC-curve.png

Отсюда следует, что оптимальным классификатором при заданных парамерах

λ−,p(y=−1) и λ+,p(y=+1)\lambda_-, p(y=-1) \text{ и }\lambda_+,p(y=+1)

будет классификатор, соответствующий точке касания изолинии потерь и ROC-кривой.

При изменении одного из этих параметров необязательно перенастраивать модель, а достаточно выбрать другую точку на ROC-кривой, т.е. взять классификатор с другим пороговым значением α\alpha.

Например, в задаче кредитного скоринга в кризис вероятность невозврата кредита p(y=−1)p(y=-1) существенно вырастает, а для адаптации к этому изменению достаточно лишь изменить порог α\alpha.