Решающие деревья
Решающее дерево (decision tree [1]) представляет собой алгоритм прогнозирования, основанный на применении иерархической системы правил. Пример простого решающего дерева для банковской задачи кредитного скоринга показан ниже:
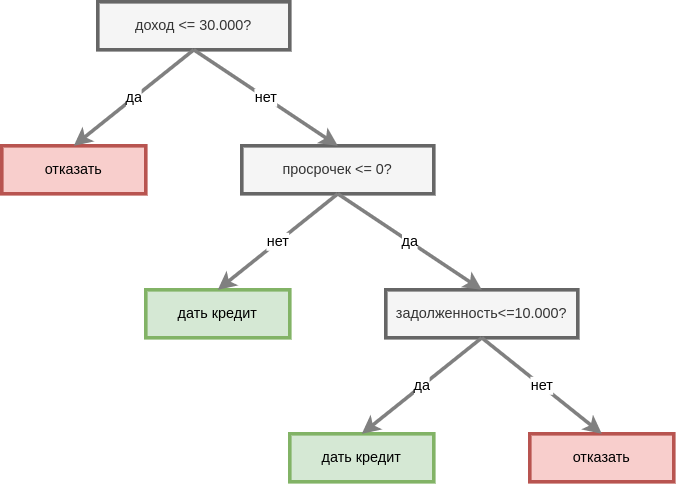
Для построения прогноза объект спускается вниз по дереву, начиная с корневой вершины. При спуске по определённому маршруту объект проходит внутренние узлы (inner nodes), а заканчивается спуск на одном из терминальных узлов (листья, terminal nodes, leaves) внизу дерева.
-
Во внутренних узлах производится проверка условия вида "признакпорог". Если условие выполнено, то осуществляется спуск в левую дочернюю вершину, а если не выполнено, то в правую, пока не дойдём до терминальной вершины.
-
Каждой терминальной вершине сопоставлен константный прогноз:
-
в случае регрессии - это число;
-
в случае классификации - это метка класса либо вектор распределения вероятностей классов.
-
Работу решающего дерева можно представить непересекающейся системой правил. Например, для дерева из иллюстрации это будет:
ЕСЛИ (доход 30.000) ИЛИ (есть просрочки) И (задолженность>10.000) ТО отказать.
ЕСЛИ (доход>30.000) ИЛИ (нет просрочек) ИЛИ (есть просрочки) И (задолженность 10.000) ТО дать кредит.
Существует целый класс правиловых алгоритмов машинного обучения (rule induction), которые строят интерпретируемые, но не очень точные прогнозы. Сейчас из них используются, в основном, только решающие деревья, недостаточную точность которых компенсируют применением не одного, а целого набора решающих деревьев (ансамбля). Построению ансамблей моделей и, в частности, алгоритму бустинга посвящены отдельные разделы учебника.
Здесь будет рассматриваться самый популярный алгоритм решающего дерева CART (classification and regression tree, [2], впервые предложен в [3]). Тем не менее, существуют и другие алгоритмы, такие как ID3 и C4.5, в которых число потомков внутренних вершин может быть больше двух, а внутри вершин могут применяться другие решающие правила.
Далее мы рассмотрим примеры и особенности работы решающих деревьев для задачи регрессии и классификации, алгоритм обучения и обрезки решающих деревьев, а также изучим, как оценивать важность признаков по решающему дереву. В конце изучим основные достоинства и недостатки этого метода.