Функции неопределённости решающих деревьев

Задача регрессии

При предсказании вещественного отклика $y\in\mathbb{R}$ в качестве функции неопределённости (impurity function) используется дисперсия откликов:

$$\phi(t)=\frac{1}{\left|I_{t}\right|}\sum_{i\in I_{t}}\left(y_{i}-\text{mean}_{i\in I_{t}}(y_{i})\right)^{2}$$

где

• $I_{t}=\{i_{1},...i_{K}\}$ - множество индексов объектов, попадающих в узел $t$,

• $K=|I_t|$ - количество таких объектов,

• $\text{mean}_{i\in I_{t}}(y_{i})$ - выборочное среднее по откликам объектов, попадающих в узел $t$.

Также используется среднее абсолютное отклонение (mean absolute deviation):

$$\phi(t)=\frac{1}{\left|I_{t}\right|}\sum_{i\in I_{t}}|y_{i}-\text{median}_{i\in I_{t}}(y_{i})|,$$

где $\text{median}_{i\in I_{t}}(y_{i})$ - выборочная медиана откликов объектов узла $t$.

Для более неопределённых данных с изменяющимся откликом обе меры неопределённости будут давать высокие значения. А в случае одинаковых откликов они будут равны нулю.

Задача классификации

Для классификации функции неопределённости $\phi(t)$ будут зависеть от вероятностей классов для объектов, попавших в узел $t$. Ниже представлены популярные варианты этих функций:

название	на английском	формула
классификационная ошибка	classification error	$1-\max\{p_1,p_2,...p_C\}$
критерий Джини	Gini	$\sum_{i=1}^{C}p_{i}(1-p_{i})$
энтропийный критерий	entropy	$-\sum_{i=1}^{C}p_{i}\ln p_{i}$

Обоснование функций неопределённости

Рассмотрим бинарную классификацию и некоторый узел дерева $t$.

Пусть вероятность положительного класса $p(y=+1|t)=p$, а отрицательного $p(y=-1|t)=1-p$.

Зависимости функций неопределённости от $p$ приведены ниже:

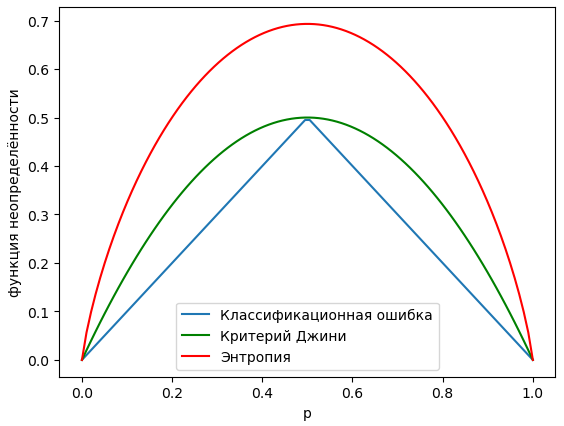
Как видим, максимальная неопределённость функций достигается в наиболее неопределённом случае, когда $p=0.5$ и оба класса равновероятны. А минимум неопределённости достигается, когда $p=0$ либо $p=1$. В этих случаях все объекты узла принадлежат одному из классов, и неопределённость классификации отсутствует.

Для многоклассового случая представленные функции также измеряют степень неопределённости классов, достигая максимума при равномерном распределении классов, когда $p_1=p_2=...=p_C=\frac{1}{C}$, а минимума, когда все объекты принадлежат одному из классов:

$$p_1=0,\, ...\, p_{i-1}=0,\, p_i=1,\, p_{i+1}=0,\, ...\, p_C=0$$

Интуитивно это можно понять следующим образом:

Классификационная ошибка измеряет ожидаемое число ошибок при классификации всех объектов максимально вероятным классом, у которого вероятность появления $p_{max}=\max \{p_1,p_2,...p_C\}$. Очевидно, что вероятность ошибки при такой классификации будет $1-p_{max}$. Классификация будет безошибочной, когда в узле присутствуют объекты только одного класса, а максимум ошибок будет достигаться, когда все классы будут равновероятны.

Критерий Джини (Gini criterion) измеряет вероятность ошибки при случайном угадывании класса по правилу:

$$\hat{y}= \begin{cases} 1,& \text{ с вероятностью }p_1, \\ 2,& \text{ с вероятностью }p_2, \\ \cdots & \cdots \\ C, & \text{ с вероятностью }p_C. \\ \end{cases}$$

Тогда, расписывая вероятность ошибки по формуле полной вероятности [1], как раз и получим критерий Джини:

$$p(\hat{y}\ne y)= \sum_{c=1}^C p(\hat{y}\ne y|y=1)p(y=1)= \sum_{c=1}^C (1-p_c)p_c$$

Эта ошибка будет максимальной, когда все классы равновероятны, и равняться нулю, когда все объекты принадлежат одному из классов.

Энтропийный критерий (entropy criterion) вычисляет энтропию случайной величины $y$:

$$y= \begin{cases} 1,& \text{ с вероятностью }p_1, \\ 2,& \text{ с вероятностью }p_2, \\ \cdots & \cdots \\ C, & \text{ с вероятностью }p_C. \\ \end{cases}$$

которая служит мерой её неопределённости. Покажем это.

Определим количество информации, которую мы получаем при случайном событии, реализующимся с вероятностью $p$, по формуле

$$\text{Info(событие с вероятностью p)}=-\ln p$$

График этой зависимости показан ниже:

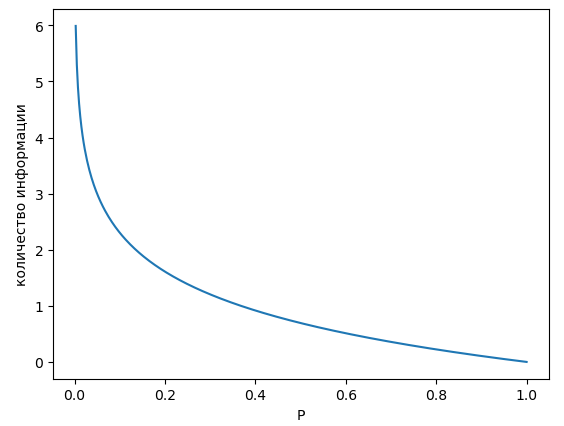
Именно так определить получаемую информацию разумно, поскольку такая функция:

• будет выдавать нулевую информацию при реализации события, у которого вероятность наступления равна 1 (происходит всегда);

• стремится к бесконечности при $p\to 0$ (событие происходит редко);

• для двух независимых событий $A$ и $B$ будет выполнено свойство аддитивности:

$$\text{Info}(A,B)=\text{Info}(A)+\text{Info}(B)$$

Тогда энтропия случайной величины $y$ будет равна ожидаемому количеству информации, которую мы получим, узнав реализацию этой случайной величины:

$$\text{entropy(y)}=\mathbb{E}\{\text{Info(y)}\} = -\sum_{c=1}^C p_c \ln p_c$$

Максимум информации мы будем получать для случая, когда все классы равновероятны, а минимум - когда реализуется всегда только один из классов.

Задача

Докажите формально, что энтропия максимизируется, когда все классы равновероятны. Для этого нужно её промаксимизировать при ограничении, что вероятности суммируются в единицу. Технически для этого используется метод множителей Лагранжа [2].

Литература

1. Wikipedia: формула полной вероятности.

2. Wikipedia: метод множителей Лагранжа.