Обрезка решающих деревьев

Идея метода

В итеративном построении решающих деревьев сверху вниз мы анализировали различные правила остановки, и был приведён пример, когда ранняя остановка может приводить к неоптимальным решениям, поскольку начальные правила разбиения не приводят к снижению неопределённости, а последующие - приводят.

Это ситуация весьма распространена на практике, поэтому для повышения точности прогнозов:

деревья строят до самого низа (пока в узлах не останется по одному объекту или все объекты листа не будут иметь один и тот же отклик);
потом обрезают лишние ветви дерева, что называется обрезкой дерева (tree pruning).

Простые подходы

В обрезке дерева его поддеревья заменяются их корнями, которые назначаются листовыми вершинами (с константным прогнозом). Делать это можно полным перебором, сравнивая качество прогнозов полного решающего дерева с обрезанным на валидационной выборке, однако придётся перебирать слишком много вариантов.

Поэтому в качестве кандидатов на обрезку можно перебирать только предпоследние вершины, потом предпредпоследние и так далее снизу вверх по дереву, однако это также требует большого числа вычислений.

Чтобы сделать поиск кандидатов на обрезку более направленным и эффективным используется алгоритм обрезки по минимальной цене.

Алгоритм обрезки по минимальной цене

В алгоритме обрезки по минимальной цене (minimal cost complexity pruning), являющегося составной частью алгоритма CART [1] дерево строится до самого низа (хотя также можно применять досрочный останов, например, по минимальному числу объектов в листьях), после чего для каждой внутренней вершины полного дерева оценивается целесообразность разрастания вершины до поддерева, сравнивая 2 ситуации:

когда эта вершина имеет под собой исходное поддерево;
когда эта вершина является терминальной (без поддерева под ним).

Эти ситуации проиллюстрированы ниже для вершины $t$ :

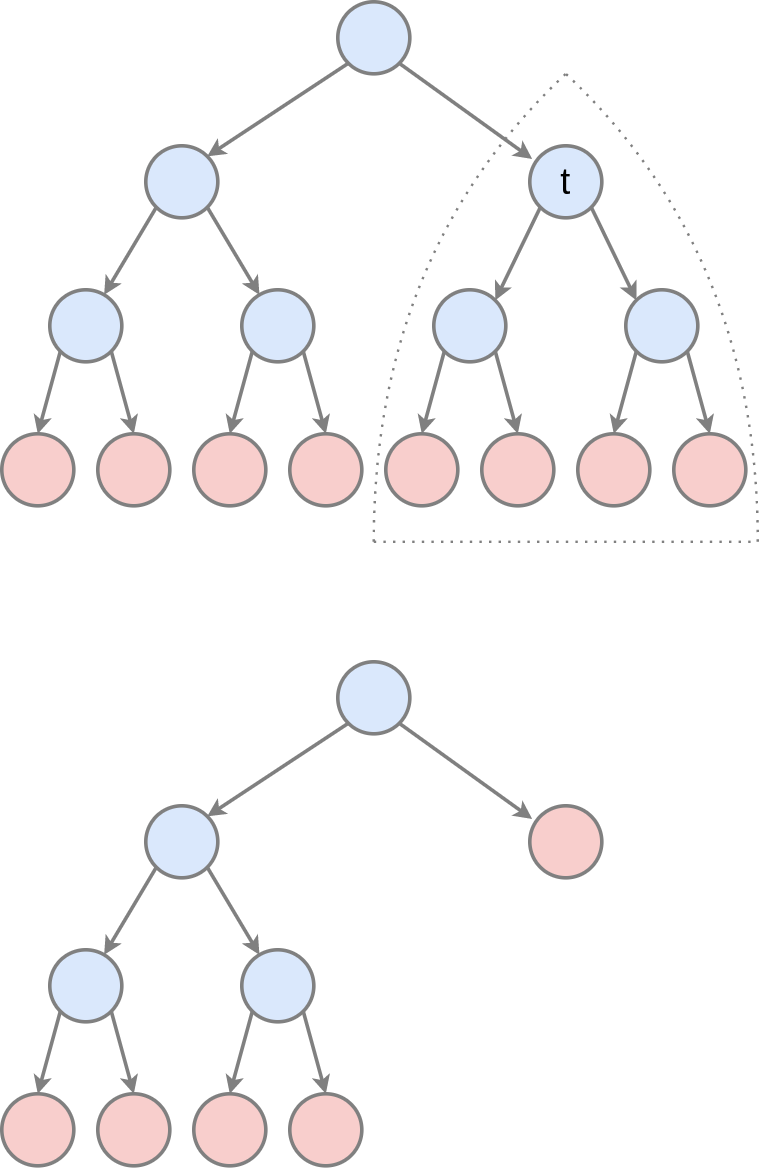
Обозначим через $A_t$ поддерево с корнем во внутренней вершине $t$ . Зададим штраф $R(A_t)$ , вычисляющий неточность прогнозов поддерева $A_t$ как среднюю функцию неопределённости в листовых вершинах поддерева $A_t$ . Например, для регрессии это может быть дисперсия откликов, а для классификации - частота ошибок. Усреднение необходимо производить пропорционально числу объектов, попадающих в каждый лист дерева.

Дополнительно определим регуляризованный штраф $R_\alpha(A_t)=R(A_t)+\alpha M(A_t)$ , который, помимо штрафа за неточность прогнозов, штрафует поддерево за сложность, вычисляемую как количество листьев $M(A_t)$ в этом поддереве. Гиперпараметр $\alpha>0$ обозначает штраф за каждый дополнительный лист поддерева.

Найдём равновесное значение $\alpha^*$ , при котором регуляризованный штраф за поддерево $A_t$ совпадёт с регуляризованным штрафом, когда поддерево $A_t$ заменяется на его корень $t$ (в котором сразу будет строиться прогноз, как на рисунке выше):

R_{\alpha^*}(A_t)=R_{\alpha^*}(t)

Это можно переписать в виде

R(A_t)+\alpha^* M(A_t)=R(t)+\alpha^*,

поскольку поддерево $t$ состоит всего из одного листа.

Отсюда равновесное $\alpha^*$ будет равно:

\alpha^*=\frac{R(t)-R(A_t)}{M(A_t)-1}

Равновесное $\alpha^*$ задаёт целесообразность разрастания внутренней вершины $t$ в поддерево $A_t$ .

Если оно равно нулю, то разрастание полностью нецелесообразно, поскольку одиночная вершина $t$ и образованное из неё поддерево $A_t$ даёт одинаковый уровень ошибок. Но чем выше $\alpha^*$ , тем построение поддерева $A_t$ целесообразнее, поскольку, чтобы компенсировать более высокую точность поддерева по сравнению с корнем, приходится сильнее штрафовать увеличение числа листов.

В алгоритме обрезки по минимальной цене вычисляются целесообразности $\alpha^*$ для каждого поддерева $A_t$ полного дерева, после чего удаляется поддерево с минимальной целесообразностью. Далее $\alpha^*$ пересчитываются для всех оставшихся вершин (достаточно пересчитывать не для всех, а только для поддеревьев, затронутых удалением с предыдущего шага), и процесс повторяется до тех пор, пока не останется одна корневая вершина исходного дерева. Таким образом, алгоритм выдаст систему вложенных друг в друга поддеревьев:

T_1\supset T_2 \supset ... \supset T_K=\text{корень первоначального дерева},

среди которых выбирается поддерево, дающее максимальную точность на валидационной выборке.

Дополнительно об алгоритмах обрезки решающих деревьях вы можете прочитать в [2]. В [3] подробно разобран пример расчёт алгоритма обрезки по минимальной цене и приведены вариации алгоритма. В [4] описано применение алгоритма в библиотеке sklearn.

Обрезка решающих деревьев

Идея метода​

Простые подходы​

Алгоритм обрезки по минимальной цене​

Литература​

Идея метода

Простые подходы

Алгоритм обрезки по минимальной цене

Литература