Бинарная логистическая регрессия

Идея метода

Логистическая регрессия (logistic regression) - это частный случай линейной классификации, когда для оценки весов используется логистическая функция потерь.

Достоинством метода является то, что он может выдавать не только метки классов, но и их вероятности.

Для удобства обозначений включим дополнительный признак, равный тождественной единице, в число признаков:

$$\begin{align*} \mathbf{x}&=[1,x^1,x^2,...x^D] \\ \mathbf{w}&=[w_0,w_1,w_2,...w_D] \end{align*}$$

Тогда линейный бинарный классификатор можно переписать в более компактном виде:

$$\hat{y}=\text{sign}(\mathbf{w}^T \mathbf{x})$$

Эквивалентно логистическая регрессия может быть переформулирована в виде вероятностной модели, выдающей вероятность положительного класса по правилу:

$$p(y=+1|\mathbf{x})=\sigma(\mathbf{w}^{T}\mathbf{x}),$$

где график сигмоидной функции $\sigma(z)$ представлен ниже:

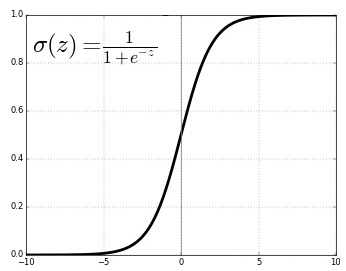
Она удовлетворяет следующему свойству:

$$1-\sigma(z)=1-\frac{1}{1+e^{-z}}=\frac{e^{-z}}{1+e^{-z}}=\frac{1}{1+e^{z}}=\sigma(-z),$$

поэтому

$$p(y=-1|\mathbf{x})=1-p(y=+1|\mathbf{x})=\sigma(-\mathbf{w}^{T}\mathbf{x})$$

Таким образом, для $y\in\{+1,-1\}$ вероятностный прогноз строится по правилу:

$$p(y|\mathbf{x})=\sigma(y \mathbf{w}^T \mathbf{x})$$

Оценим $\mathbf{w}$ методом условного максимального правдоподобия:

$$P(Y|X)=\prod_{n=1}^{N}p(y_{n}|\mathbf{x}_{n})=\prod_{n=1}^{N}\sigma(\mathbf{w}^T \mathbf{x}_{n} y_{n})=\prod_{n=1}^{N}\frac{1}{1+e^{-\mathbf{w}^T \mathbf{x}_{n} y_{n}}}\to\max_{\mathbf{w}}$$

Поскольку максимизация положительной функции эквивалентна минимизации обратной к ней, то исходная задача эквивалентна следующей:

$$\prod_{n=1}^{N}\left(1+e^{-\mathbf{w}^T \mathbf{x}_{n} y_{n}}\right)\to\min_{\mathbf{w}}$$

Прологарифмировав критерий, получим классическую задачу минимизации эмпирического риска с логистической функцией потерь (logistic loss):

$$\sum_{n=1}^{N}\log_{2}(1+e^{-\mathbf{w}^T \mathbf{x}_{n} y_{n}})\to\min_{\mathbf{w}}$$

Пример запуска в Python

Логистическая регрессия для бинарной классификации:

from sklearn.linear_model import LogisticRegression
from sklearn.metrics import brier_score_loss
from sklearn.metrics import accuracy_score

X_train, X_test, Y_train, Y_test = get_demo_classification_data()  
model = LogisticRegression(C=1, penalty='l2')    # инициализация модели, (1/C) - вес при регуляризаторе
model.fit(X_train, Y_train)     # обучение модели   
Y_hat = model.predict(X_test)   # построение прогнозов
print(f'Точность прогнозов: {100*accuracy_score(Y_test, Y_hat):.1f}%')  

P_hat = model.predict_proba(X_test)  # можно предсказывать вероятности классов

loss = brier_score_loss(Y_test, P_hat[:,1])  # мера Бриера на вероятности положительного класса
print(f'Мера Бриера ошибки прогноза вероятностей: {loss:.2f}')  

Больше информации. Полный код.

Настраивать логистическую регрессию можно различными численными методами. Их сравнение приводится в [1]. В следующей главе мы рассмотрим обобщение логистической регрессии для решения задачи многоклассовой классификации.

Больше информации о логистической регрессии вы можете прочитать в [2], [[3]](Дьяконов А.Г. Машинное обучение и анализ данных: линейные классификаторы.) и [4].

Литература

1. Minka T. P. A comparison of numerical optimizers for logistic regression //Unpublished draft. – 2003. – С. 1-18.