Оценка весов линейного классификатора

Отступ линейного бинарного классификатора

Как выводилось ранее, отступ бинарного классификатора $\hat{y}=\text{sign}(g(\mathbf{x}))$ с относительной дискриминантной функцией $g(\mathbf{x})$ определяется как

$$M(\mathbf{x},y)=yg(\mathbf{x})$$

В случае линейного бинарного классификатора $\hat{y}=\text{sign}(w_0+\mathbf{w}^T\mathbf{x})$ он записывается как

$$M(\mathbf{x},y)=y(w_0+\mathbf{w}^T \mathbf{x}),$$

где $y\in\{+1,-1\}$.

По смыслу отступ служит непрерывной мерой качества классификации объекта $(\mathbf{x},y)$ - чем он выше, тем классификация лучше. Если $M(\mathbf{x},y)>0$, то классификация корректна, а если $M(\mathbf{x},y)<0$, то некорректна.

Численная оценка весов линейного бинарного классификатора

Как подобрать оптимальные параметры $w_0$ и $\mathbf{w}$? В общем случае оптимальные веса нельзя найти аналитически, поэтому для их нахождения используются численные методы.

Их можно было бы подбирать таким образом, чтобы минимизировать число неправильных классификаций, что эквивалентно критерию

$$\frac{1}{N}\sum_{n=1}^N \mathbb{I}\{M(\mathbf{x}_n,y_n) \le 0\}=\frac{1}{N}\sum_{n=1}^N \mathcal{L}(M(\mathbf{x}_n,y_n)) \to \min_{w_0,\mathbf{w}}$$

c функцией потерь $\mathcal{L}(\mathbf{x}_n,y_n)=\mathbb{I}\{y_n(w_0+\mathbf{w}^T \mathbf{x}_n)\le 0\}$.

Однако эта функция принимает всего два значения: единицу с одной стороны разделяющей гиперплоскости $w_0+\mathbf{w}^T \mathbf{x}=0$ и ноль с другой. В результате критерий получится кусочно-постоянной (ступенчатой) функцией, у которой почти всюду градиент по весам будет равен нулю, вследствие чего мы не сможем найти веса численными методами, основанными на градиенте функции!

Поэтому на практике используется не представленная выше кусочно-постоянная функция потерь, а другие гладкие (непрерывно-дифференцирируемые) функции с невырожденными градиентами на широком спектре значений.

Основные функции потерь

Основные функции потерь, используемые для настройки линейных бинарных классификаторов, приведены ниже:

название	английское название	формула $\mathcal{L}(M)$
экспоненциальная	exponential	$e^{-M}$
функция персептрона	perceptron	$[-M]_{+}$
шарнирная	hinge	$[1-M]_{+}$
логистическая	logistic	$\log_{2}\left(1+e^{-M}\right)$

Графики функций потерь показаны ниже:

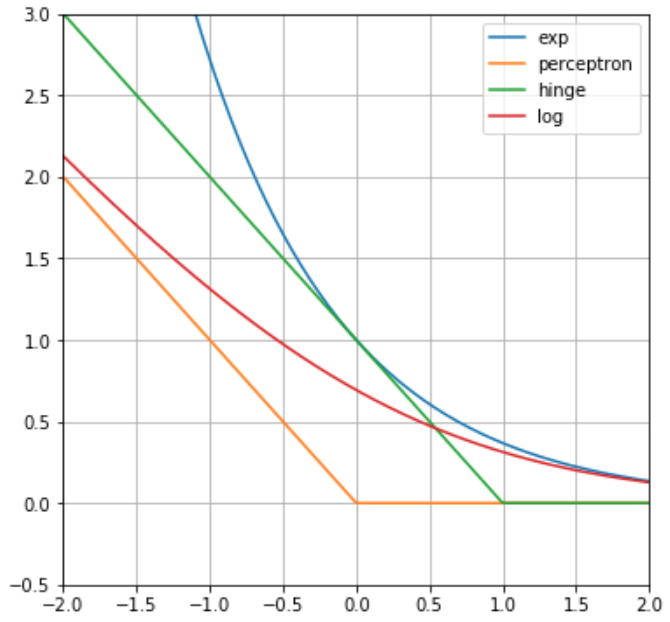
Какая из представленных функций остановит обучение весов сразу, как только точность классификации достигнет 100% точности на обучающей выборке?

Функция персептрона, поскольку для верно классифицированных объектов отступ $M$ будет положителен, а функция потерь станет равной нулю. Это не является оптимальной стратегией, поскольку граница между классами может пройти очень близко к объектам, а новые объекты тестовой выборки могут попадать уже с неверной стороны от разделяющей гиперплоскости и неверно классифицироваться.

Другие же функции потерь продолжат обучение, чтобы провести линейную гиперплоскость дальше даже от верно классифицированных объектов. В результате они окажутся глубже в областях своих классов. И при появлении новых объектов, похожих на обучающие, они всё равно будут классифицироваться правильно.

Какая из представленных функций наименее устойчива к [нетипичным объектам-выбросам](../Data-preprocessing/Outlier-filtering)?

Объект-выброс лежит далеко от основной массы объектов и, соответственно, будет, скорее всего, лежать далеко от разделяющей гиперплоскости и иметь высокий отступ по абсолютной величине. А если он неверно классифицируется, то отступ будет большим по модулю и отрицательным. Сильнее всего это будет штрафоваться экспоненциальной функцией потерь. Поэтому эта функция потерь не рекомендуется на практике, если в выборке могут быть нетипичные объекты-выбросы.

Регуляризация

Как и в случае линейной регрессии, при настройке линейных классификаторов рекомендуется использовать регуляризацию:

$$\frac{1}{N}\sum_{n=1}^N \mathcal{L}(M(\mathbf{x}_n,y_n)) {\color{red}+\lambda R(\mathbf{w})} \to \min_{w_0,\mathbf{w}}$$

Гиперпараметр $\lambda>0$ контролирует сложность (гибкость) модели. L1- и ElasticNet-регуляризации способны отбирать признаки, зануляя часть коэффициентов при признаках, а L2-регуляризация - нет. Однако L2-регуляризация равномернее распределяет влияние на отклик похожих признаков.

Влияние масштаба признаков

Прогнозы линейного классификатора без регуляризации не зависят от масштабирования признаков (при последующей перенастройке модели). Но если использовать регуляризацию, то больший эффект начинают оказывать признаки с большим разбросом значений.

Почему?

Потому что признакам с малым разбросом будут соответствовать более высокие по модулю значения весов, которые будут сильнее подвергаться регуляризации и прижиматься к нулю. Поэтому соответствующие признаки будут влиять на прогноз слабее.

В связи с этим рекомендуется предварительное приведение всех вещественных признаков к одному масштабу одним из методов нормализации признаков.

---

Далее мы рассмотрим частные случаи бинарного классификатора - метод опорных векторов и логистическую регрессию, после чего обобщим логистическую регрессию на многоклассовый случай. В отдельном разделе учебника будут рассмотрены методы численной настройки параметров моделей.

Дополнительно погрузиться в тему вы можете, прочитав соответствующие главы учебника ШАД [1] и учебника А.Г. Дьяконова [2].

Литература

1. Учебник ШАД: линейные модели.

2. Дьяконов А.Г. Машинное обучение и анализ данных: линейные классификаторы.