Функции расстояния

Преимуществом метрических методов является то, что их можно применять с любой функцией расстояния (distance function) между объектами $\rho(\mathbf{x},\mathbf{z})$. По смыслу расстояние измеряет непохожесть объектов между собой, и его не надо путать с функцией похожести (similarity function) $S(\mathbf{x},\mathbf{z})$, принимающей более высокие значения между более похожими объектами.

Взаимосвязь расстояния и похожести

Мы всегда можем преобразовать расстояние в похожесть и наоборот, применяя некоторую убывающую функцию $K(\cdot)$:

$$S(\mathbf{x},\mathbf{z})=K(\rho(\mathbf{x},\mathbf{z}))$$

Например, $S(\mathbf{x},\mathbf{z})=1-\rho(\mathbf{x},\mathbf{z})$ или $S(\mathbf{x},\mathbf{z})=1/\rho(\mathbf{x},\mathbf{z})$.

Сравнение векторов вещественных чисел

Если $\mathbf{x},\mathbf{z}\in\mathbb{R}^D$, то часто используются следующие функции расстояния:

Название	$\rho(\mathbf{x},\mathbf{z})$
Евклидово	$\sqrt{\sum_{i=1}^{D}(x^{i}-z^{i})^{2}}$
$L_1$ (Манхэттенская)	$\sum_{i=1}^{D}\lvert x^{i}-z^{i}\rvert$
$L_{\infty}$	$\max_{i=1,2,...D}\lvert x^{i}-z^{i} \rvert$
$L_p$	$\sqrt[p]{\sum_{i=1}^{D}\left\lvert x^{i}-z^{i}\right\rvert^{p}}$
Канберра	$\frac{1}{D}\sum_{i=1}^{D}\frac{\lvert x^{i}-z^{i}\rvert}{\left\lvert x^{i}\right\rvert+\left\lvert z^{i}\right\rvert}$
Ланса-Уильямса	$\frac{\sum_{i=1}^{D}\vert x^{i}-z^{i}\vert}{\sum_{i=1}^{D}\left\vert x^{i}+z^{i}\right\vert}$

Косинусная мера близости

Очень популярна косинусная мера близости [1]:

$$S(\mathbf{x},\mathbf{z})=\frac{\mathbf{x}^{T}\mathbf{z}}{\left\lVert \mathbf{x}\right\rVert \left\lVert \mathbf{z}\right\rVert }=\frac{\sum_{i=1}^{D}x^{i}z^{i}}{\sqrt{\sum_{i=1}^{D}\left(x^{i}\right)^{2}}\sqrt{\sum_{i=1}^{D}\left(z^{i}\right)^{2}}},$$

измеряющая косинус угла между векторами $\mathbf{x}$ и $\mathbf{z}$, поэтому принимающая значения на отрезке $[-1,1]$.

Согласно этой мере объекты близки, если угол между ними мал, а, соответственно, косинус этого угла близок к единице. Косинусная мера близости не зависит от длин сравниваемых векторов (докажите!).

Это полезно в некоторых приложениях, таких как анализ текстов, кодируемых счётчиками встречаемости в них слов. Если продублировать документ, то счётчики всех слов увеличатся вдвое, как и длина вектора признаков, кодирующего документ. Поскольку дублирование текста не оказывает влияние на смысл документа, то оно не должно изменять попарные расстояния между документами, что и наблюдается для косинусной меры близости.

Расстояние Махаланобиса

Для сравнения векторов, элементы которых сильно скоррелированы между собой, используется Евклидово расстояние, но не между исходными объектами $\mathbf{x},\mathbf{z}$, а между их декоррелированными версиями:

$$\mathbf{x}'=\Sigma^{-1/2}(\mathbf{x}-\bm{\mu}), \mathbf{z}'=\Sigma^{-1/2}(\mathbf{z}-\bm{\mu}), \text{ где } \Sigma^{-1/2}=(\Sigma^{-1})^{1/2}=(\Sigma^{1/2})^{-1}$$

Задача

Докажите, что $\mathbf{x}'$ и $\mathbf{z}'$ будут иметь нулевое среднее и единичную матрицу ковариаций, т.е. отдельные элементы векторов будут не скоррелированы между собой.

Графически процесс перевода из скоррелированного пространства (A) в декоррелированное (B) показан ниже:

В терминах исходных векторов это расстояние выражается как

$$\rho(\mathbf{x},\mathbf{z})=\sqrt{(\mathbf{x}-\mathbf{z})^{T}\Sigma^{-1}(\mathbf{x}-\mathbf{z})}$$

и называется расстоянием Махаланобиса [2].

Задача

Докажите, что Евклидово расстояние между декореллированными версиями объектов $\mathbf{x}$ и $\mathbf{z}$ будет считаться по формуле выше.

В более общем случае расстояние можно определить через произвольную неотрицательно-определённую матрицу $M$, которую можно настраивать по данным (metric learning [3]):

$$\rho(\mathbf{x},\mathbf{z})=\sqrt{(\mathbf{x}-\mathbf{z})^{T}M(\mathbf{x}-\mathbf{z})}$$

Сравнение бинарных векторов

Для бинарных векторов, состоящих только из нулей и единиц, часто используют расстояние Хэмминга [4]:

$$\rho(\mathbf{x},\mathbf{z})=\sum_{n=1}^N \mathbb{I}\{x^i \ne z^i\}$$

Сравнение множеств

Для сравнения двух множеств X и Z (например наборов товаров, купленных в магазине по двум чекам) используется мера близости Жаккара (Jaccard index [5]), равная числу элементов в пересечении множеств, нормированному на число элементов в их объединении:

$$S(X,Z)=\frac{\vert X \cap Z\vert}{\vert X \cup Z \vert}$$

Мера принимает значения в отрезке $[0,1]$.

Сравнение строк

Для сравнения строк часто используется редакторское расстояние (edit distance), называемое также расстоянием Левенштейна (Levenstein distance [6], предложена в [7]). Для двух строк $x$ и $z$ оно вычисляется как минимальное число операций вставки символа, удаления символа и замены одного символа другим, необходимое для перевода одной строки в другую. Например, расстояние между строками "вагон" и "авто" будет 4, поскольку минимально требуется 4 операции для преобразования одной строки в другую:

	операция	результат
		ВАГОН
1	удаление В	АГОН
2	замена Г на В	АВОН
3	вставка Т	АВТОН
4	удаление Н	АВТО

Строки могут быть произвольной длины, содержать пробелы и описывать целые тексты!

Существует эффективный алгоритм, позволяющий найти минимальное количество редакторских операций за полиномиальное время от длин строк [8], предложенный в [9].

Сравнение временных рядов

Временные ряды можно сравнивать как вектора их последовательных значений, но только в случае, когда они состоят из одинакового количества элементов. Перед сравнением может применяться приведение их значений к одному масштабу (например, нулевое среднее и единичная дисперсия).

Также динамику рядов можно раскладывать по базису некоторых функций, а ряды представлять в виде коэффициентов разложения по базису и сравнивать обычными функциями расстояния между векторами признаков.

Если временные ряды разные по длительности, то можно более короткий временной ряд растянуть до длины более длинного временного ряда.

Альтернативно можно использовать алгоритм динамической трансформации временной шкалы (dynamic time warping [10]), в котором перед сравнением ищется оптимальное локальное растяжение участков каждого из рядов, чтобы они лучше подходили друг к другу, как показано ниже на рисунке справа (источник):

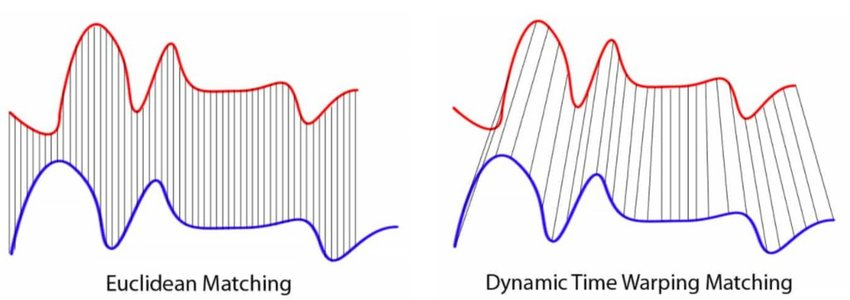
Этот алгоритм позволяет сравнивать временные ряды разной длины по наличию в них схожей динамики, даже если она происходила с разной скоростью. Расчёт расстояния также может быть эффективно произведён за полиномиальное время от длин сравниваемых рядов.

Литература

1. Wikipedia: cosine similarity.

2. Wikipedia: Mahalanobis distance.

3. Kulis B. et al. Metric learning: A survey //Foundations and Trends® in Machine Learning. – 2013. – Т. 5. – №. 4. – С. 287-364.

4. Wikipedia: Hamming distance.

5. Wikipedia: Jaccard index.

6. Wikipedia: Levenshtein distance.

7. Левенштейн В. И. Двоичные коды с исправлением выпадений, вставок и замещений символов //Доклады Академии наук. – Российская академия наук, 1965. – Т. 163. – №. 4. – С. 845-848.

8. Wikipedia: edit distance.

9. Kukich K. Techniques for automatically correcting words in text //ACM computing surveys (CSUR). – 1992. – Т. 24. – №. 4. – С. 377-439.

10. Wikipedia: dynamic time warping.