Метод K ближайших соседей

Идея метода

Метод K ближайших соседей (K nearest neighbors, [1]) умеет решать как задачу классификации, так и задачу регрессии. Обучение метода заключается лишь в сохранении обучающих объектов в памяти. На этапе построения прогноза для объекта $\mathbf{x}$ ищутся $K$ ближайших к нему объектов обучающей выборки ("ближайшие соседи"), после чего

• для классификации: назначается самый частый класс среди $K$ ближайших объектов;

• для регрессии: назначается средний отклик по откликам среди $K$ ближайших объектов.

Иллюстрация для двумерного пространства признаков и задачи регрессии приведена ниже:

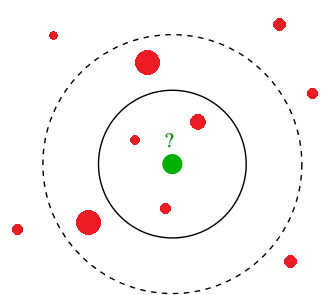
Каждый объект обучающей выборки обозначен красным шаром, а радиус шара - величина отклика. Требуется построить прогноз для тестового объекта, обозначенного зелёным шаром. Его отклик (радиус) определяется средним значением откликов (радиусов) среди K ближайших объектов.

Выбор $K$ влияет на результат. Например, увеличение $K$ с 3 до 5 приводит к увеличению прогноза.

На следующем рисунке показана иллюстрация для задачи классификации. Класс обозначен цветом и формой. Требуется построить прогноз для объекта, обозначенного зелёным шаром.

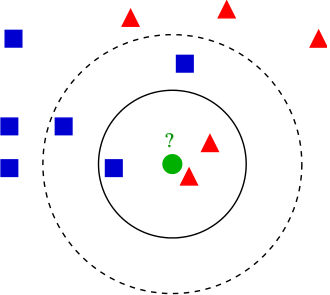
Здесь также видно, что выбор $K$ влияет на результат. При $K=3$ целевому объекту будет назначен красный класс, а при $K=5$ - уже синий.

Прогноз вероятностей классов

Метод K ближайших соседей может выдавать и вероятности классов. Для этого достаточно усреднить частоты попадания классов в число ближайших соседей.

Анализ метода

Рассмотрим работу метода для задачи классификации двумерных объектов с различным выбором гиперпараметра $K$.

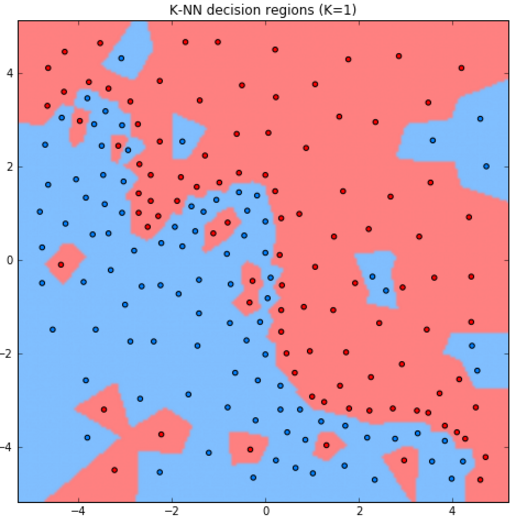
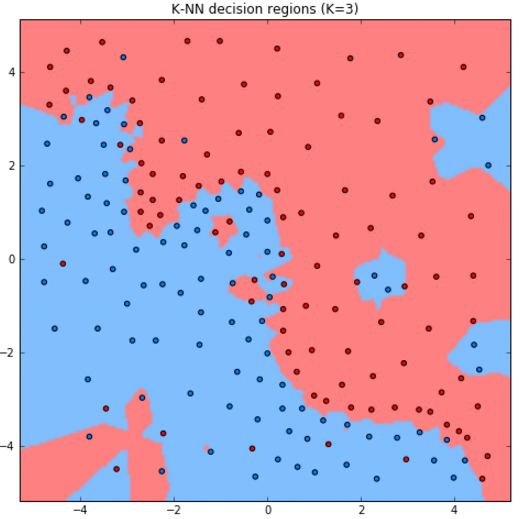
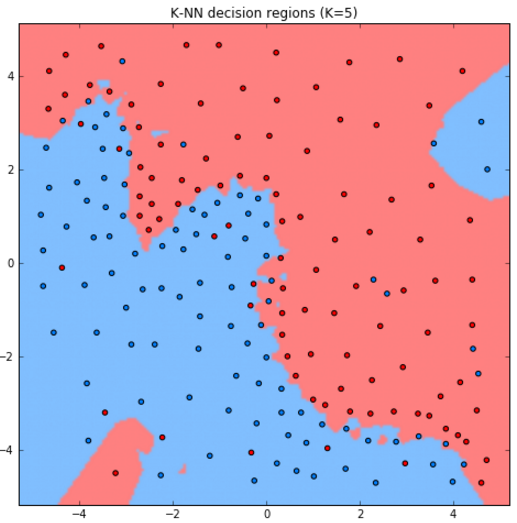
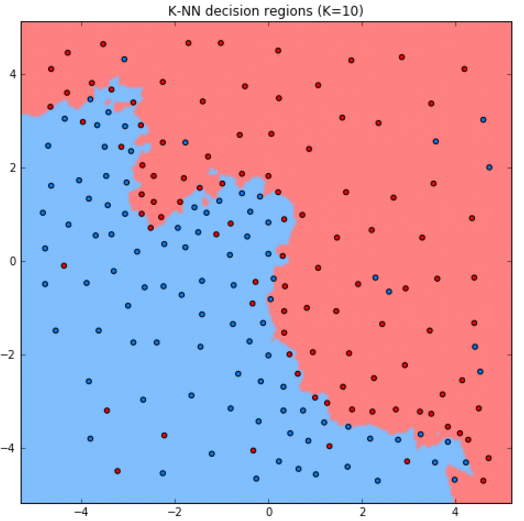
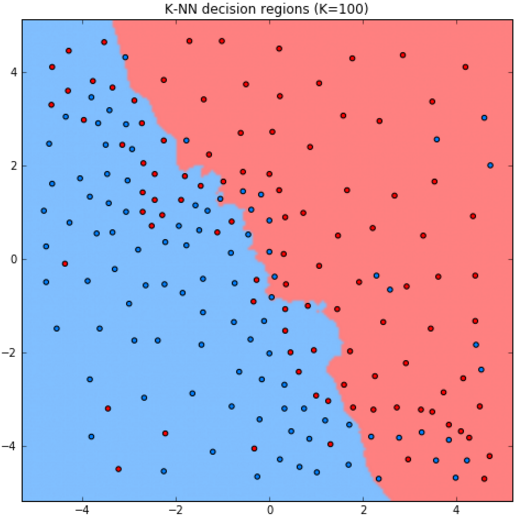
Как видим, при увеличении $K$ модель становится более простой (менее гибкой), поскольку усреднение производится по более широкой окрестности объектов.

Как будет работать метод при K=N?

При K=N в качестве прогноза будет производиться агрегация сразу по всем объектам выборки, и метод выродится в константный прогноз, назначающий всем объектам самый распростаранённый класс в обучающей выборке.

В качестве другого примера рассмотрим задачу регрессии по одному признаку, где истинный отклик генерируется по формуле $y=\sin x+\varepsilon$, а $\varepsilon$ - случайный нормально распределённый шум. Обучающие объекты обозначены черными точками, а целевая зависимость - пунктирной линией. Сплошной линией обозначен прогноз метода $K$ ближайших соседей при различных значениях гиперпараметра $K$.

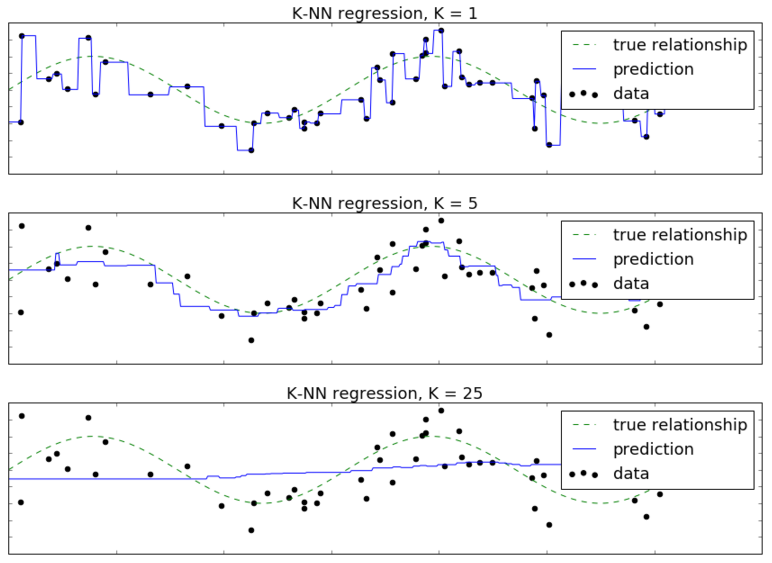
Здесь также видно, что при малом $K$ метод чересчур гибкий и переобучается под шум в данных. А при больших $K$ - недостаточно гибкий и недообучается.

Почему гиперпараметр K нельзя подбирать по обучающей выборке?

Гиперараметр K определяет гибкость модели. Чем он ниже, тем модель получается более гибкой и тем точнее настраивается на данные. Соответственно, при выборке $K$ на основе обучающей выборки всегда будет оказываться, что наилучшим значением параметра будет $K=1$, при котором достигается 100% точность. Поэтому $K$ и является гиперпараметром (а не параметром, подбираемым на обучающей выборке), и выбирать его следует только на основе прогнозов на внешней валидационной выборке.

При $K=1$ метод называется методом ближайшего соседа (nearest neighbor method).

Родственный метод

В качестве альтернативы можно усреднять не по фиксированному числу ближайших объектов, а по всем объектам, попавшим в $\varepsilon$-окрестность целевого объекта $\mathbf{x}$, сколько бы их ни оказалось (radius nearest neighbor). В чем-то этот метод логичнее, поскольку позволяет контролировать похожесть объектов, по которым будет строиться прогноз.

Однако он используется реже в связи со сложностью выбора радиуса окрестности $\varepsilon$. Если она слишком велика, то будет производиться усреднение по избыточному количеству объектов. А если слишком мала, то в окрестность может не попасть ни один объект!

Указанный метод также допускает обобщение на произвольную функцию расстояния.

Более детально о теории метода ближайших соседей можно прочитать в [2], а также в документации библиотеке sklearn [3] вместе с описанием реализации. Также идея метода и основные методы повышения скорости его работы описаны в учебнике ШАД [4].

Пример запуска в Python

Метод K ближайших соседей для классификации:

from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import accuracy_score
from sklearn.metrics import brier_score_loss

X_train, X_test, Y_train, Y_test = get_demo_classification_data()  
model = KNeighborsClassifier(n_neighbors=3)  # инициализация модели
model.fit(X_train,Y_train)                   # обучение модели                
Y_hat = model.predict(X_test)                # построение прогнозов
print(f'Точность прогнозов: {100*accuracy_score(Y_test, Y_hat):.1f}%')  

P_hat = model.predict_proba(X_test)  # можно предсказывать вероятности классов

loss = brier_score_loss(Y_test, P_hat[:,1])  # мера Бриера на вер-ти положительного класса
print(f'Мера Бриера ошибки прогноза вероятностей: {loss:.2f}')

Больше информации. Полный код.

Метод K ближайших соседей для регрессии:

from sklearn.neighbors import KNeighborsRegressor
from sklearn.metrics import mean_absolute_error

X_train, X_test, Y_train, Y_test = get_demo_regression_data()  
model = KNeighborsRegressor(n_neighbors=3)  # инициализация модели
model.fit(X_train,Y_train)                  # обучение модели                
Y_hat = model.predict(X_test)               # построение прогнозов
print(f'Средний модуль ошибки (MAE): \
            {mean_absolute_error(Y_test, Y_hat):.2f}')   

Больше информации. Полный код.

Далее мы проанализируем достоинства и недостатки метода K ближайших соседей, рассмотрим его обобщение, при котором ближайшие объекты по-разному будут влиять на прогноз, а также рассмотрим основные функции расстояния в машинном обучении.

Литература

1. Wikipedia: k-nearest neighbors algorithm.
2. Webb A. R., Copsey K.D. Statistical pattern recognition. – John Wiley & Sons, 2011: k-nearest-neighbour method.
3. Документация sklearn: nearest neighbors.
4. Учебник ШАД: метрические методы.