Веса в метрических методах

Веса $w_i$ с которыми учитываются ближайшие соседи, должны быть неотрицательными и убывать с ростом расстояния до ближайшего соседа.

Их можно сделать зависимыми от порядкового номера $k\in\{1,2,...K\}$ ближайшего соседа:

$$w_{k}=\alpha^{k},\quad\alpha\in(0,1) - \text{гиперпараметр}$$

Тогда они будут убывать по экспоненциальному закону от порядкового номера соседа.

Также их можно сделать убывающими по линейному закону:

$$w_{k}=\frac{K+1-k}{K}$$

Более естественно сделать веса зависящими от расстояния до ближайшего соседа $\rho(\mathbf{x},\mathbf{x}_k)$, а не от его порядкового номера. Пусть $(\mathbf{x}_{1},y_{1}),(\mathbf{x}_{2},y_{2}),...(\mathbf{x}_{K},y_{K})$ - ближайшие соседи в обучающей выборке для целевого объекта $\mathbf{x}$, для которого мы строим прогноз.

Веса можно сделать убывающими по гиперболическому закону:

$$w_{k}=\frac{1}{\rho(\mathbf{x}_{k},\mathbf{x})}$$

В чём недостаток такого выбора весов и как его исправить?

При приближении к соседу его вес будет неограниченно возрастать, в результате чего отклик на этом объекте начнёт перевешивать отклики на других соседях. Чтобы воспрепятствовать неограниченному возрастанию весов, нужно его ограничить сверху некоторой константой $M>0$:

$$w_{k}=\min\left\{ M; \frac{1}{\rho(\mathbf{x}_{k},\mathbf{x})} \right\}$$

Также можно сделать веса убывающими по линейному закону:

$$w_{i}=\begin{cases} \frac{\rho(\mathbf{x}_{K},\mathbf{x})-\rho(\mathbf{x}_{i},\mathbf{x})}{\rho(\mathbf{x}_{K},\mathbf{x})-\rho(\mathbf{x}_{1},\mathbf{x})}, & \rho(\mathbf{x}_{K},\mathbf{x})\ne\rho(\mathbf{x}_{1},\mathbf{x})\\ 1 & \rho(\mathbf{x}_{K},\mathbf{x})=\rho(\mathbf{x}_{1},\mathbf{x}) \end{cases}$$

В более общем виде веса определяются по формуле:

$$w_i=K\left(\frac{\rho(\mathbf{x},\mathbf{x}_i)}{h}\right)$$

для некоторой убывающей функции $K(\cdot)$, называемой ядром (kernel) и зависящей от расстояния между объектами $\rho(\mathbf{x},\mathbf{x}_i)$, нормированной на параметр ширины окна $h$ (bandwidth), который в общем случае представляет собой не константу, а тоже функцию от $\mathbf{x}$.

Графики популярных ядер $K(\cdot)$ приведены ниже вместе с формулами для их расчёта (источник).

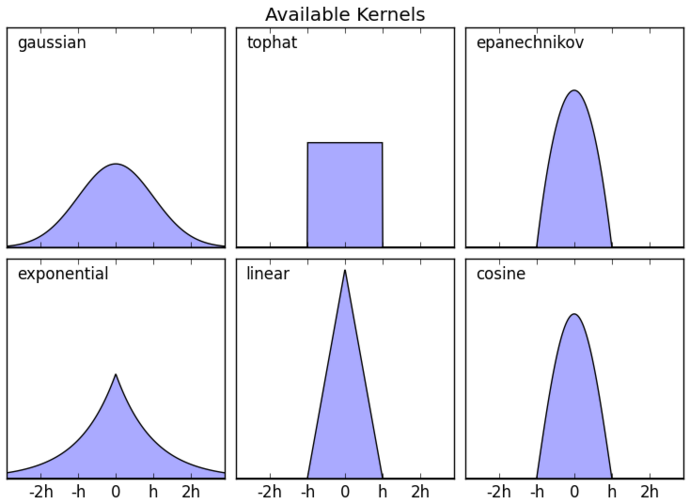
Ядро	Формула
top-hat	$\mathbb{I}[\vert u \vert<1]$
линейное	$\max\{0,1-\vert u \vert\}$
Епанечникова	$\max\{0,1-u^{2}\}$
экспоненциальное	$e^{-\vert u \vert}$
Гауссово	$e^{-\frac{1}{2}u^{2}}$
квартическое	$(1-u^{2})^{2}\mathbb{I}[\vert u \vert<1]$

Гиперпараметр ширины окна $h$ определяет, насколько сильно меняются веса при изменении расстояний до объектов. Чем $h$ выше, тем слабее веса зависят от расстояний, а при $h\to\infty$ веса стремятся к равномерным, и взвешенный метод ближайших соседей стремится к обычному (без весов).

Ширину окна можно варьировать в зависимости от целевого объекта, поэтому в общем случае она записывается как $h(\mathbf{x})$.