Латентный семантический анализ

Методы, основанные на совстречаемости слов, выдают эмбеддинги длины $S$ (число уникальных слов словаря). При раздельном учёте левого и правого контекста эмбеддинг будет размера $2S$. Поскольку число уникальных слов велико, то эмбеддинги будут получаться очень длинными, а работа с такими длинными эмбеддингами будет неэффективной, поскольку

• потребуется много вычислений,

• полученная перепараметризованная модель будет переобучаться.

Поэтому после получения высокоразмерного эмбеддинга его сжимают до значительно более низкой размерности $D\sim 300$.

Усечённое сингулярное разложение

Для этого к матрице совстречаемости $M$ применяют усечённое сингулярное разложение (truncated singluar values decomposition, truncated SVD [1]), являющееся наиболее точным низкоранговым приближением исходной матрицы по норме Фробениуса [2]:

$$M \approx U\cdot \Sigma \cdot V^T, \quad U^T\cdot U = I, \; V^T\cdot V = I, \Sigma=\text{diag}\{\sigma_1, \sigma_2, ...\sigma_D\},$$

где $I$ обозначает единичную матрицу размера $D\times D$, а $\text{diag}\{\sigma_1,\sigma_2,...\sigma_D\}$ - диагональную с элементами $\sigma_1\ge \sigma_2\ge...\ge\sigma_D\ge0$, называемыми сингулярными числами (singluar values).

Размеры соответствующих матриц: $U,V\in\mathbb{R}^{S\times D},\Sigma\in\mathbb{R}^{D\times D}$, а $D$ является выбираемым гиперпараметром.

Чем $D$ выше, тем приближение матрицы будет менее экономичным, зато более точным. Безошибочная точность достигается, когда $D$ больше либо равна ранга матрицы $M$.

Графически сингулярное разложение можно представить следующим образом (рядом с каждой матрицей указан её размер):

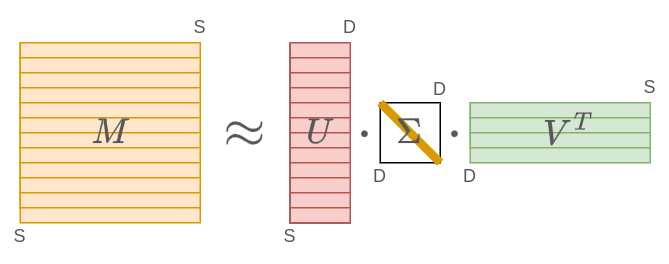
Интуиция сингулярного разложения

В методах совстречаемости $i$-му слову соответствует $i$-й полноразмерный эмбеддинг в виде $i$-й строки матрицы $M$. Из сингулярного разложения следует, что все эмбеддинги представляются линейной комбинацией строк матрицы $V^T$. Можно показать, что это первые $D$ главных компонент [3] для эмбеддингов всех слов. Интуитивно эти строки показывают основные темы или высокоуровневые смысловые концепции, линейно комбинируя которые, можно получить эмбеддинг любого слова с высокой точностью.

Например, при анализе новостей такими концепциями могут быть темы политики, экономики, спорта, культуры и т.д.

$i$-й элемент матрицы $\Sigma$ будет весом, на который домножается каждая тема. По смыслу этот коэффициент показывает важность темы для восстановления полноразмерных эмбеддингов (состоящих из всех слов).

А $i$-ая строка матрицы $U$ будет обозначать коэффициенты, с которыми каждую из тем нужно сложить/вычесть, чтобы (приближённо) получить исходный полноразмерный эмбеддинг.

Построение низкоразмерных эмбеддингов

Чтобы эффективно представить $i$-ое слово, достаточно перейти от его полноразмерного эмбеддинга к сокращённому - $i$-й строке матрицы $U$.

По сути при этом мы перейдём от описания слова по контекстным словам, с которыми оно часто встречается, к его описанию в терминах семантически высокоуровневых тем, к которым оно принадлежит. Такой подход называется латентным семантическим анализом (Latent Semantic Analysis, LSA).

Классический LSA

Более часто подход LSA используется не для построения эмбеддингов слов, а для построения эмбеддингов документов:

1. Каждый документ представляется $S$-мерным эмбеддингом по тому, насколько часто в нём встречается каждое слово языка (в виде счётчиков встречаемости, частоты встречаемости либо TF-IDF [4] представления).

2. Эти эмбеддинги конкатенируются в матрицу $M\in\mathbb{R}^{N\times S}$, где $N$ - число документов.

3. Далее точно так же к матрице $M$ применяется метод LSA, в результате которого каждый документ кодируется уже сокращенным $D$-мерным эмбеддингом, представляющим собой степени представленности каждой темы уже не в слове, а в документе среди тем, заданных строками матрицы $V^T$.

---

Пока мы изучили построение эмбеддингов слов методами классического машинного обучения. Далее мы изучим нейросетевой подход Word2vec для построения эмбеддингов слов, а также нейросетевой метод для построения эмбеддингов целых параграфов в тексте.

Литература

1. Wikipedia: Сингулярное разложение.
2. Wikipedia: Норма матрицы.
3. Wikipedia: Метод главных компонент.
4. Wikipedia: TF-IDF.