Оптимизация Skip-Gram

Для качественной настройки эмбеддингов слов в модели Skip-Gram её нужно настраивать на гигантских коллекциях текстовых данных (100 миллионов слов и больше). Это связано с вычислительными трудностями, поскольку при расчёте вероятностей каждого слова приходится вычислять знаменатель следующей дроби:

$$p(w_{t+i}|w_{t})=\frac{\exp\left(u_{w_{t}}^{T}v_{w_{t+i}}\right)}{{\color{red}\sum_{w=1}^{S}\exp\left(u_{w_{t}}^{T}v_{w}\right)}},$$

равный сумме величин для всех уникальных слов языка $S$, а их очень много!

Поэтому для ускорения настройки Skip-Gram используются специальные вычислительно эффективные методы - иерархический SoftMax либо негативное сэмплирование [1].

CBOW

В модели CBOW присутствует такая же проблема и для её оптимизации используются свои усовершенствованные методики оптимизации. Здесь они не рассматриваются, т.к. на практике в основном используется Skip-Gram как более эффективная, т.к. в ней контекст вычисляется по одному слову, а не по совокупности.

Иерархический SoftMax

В методе Hierarchical SoftMax строится бинарное дерево, каждому листу которого ставится в соответствие уникальное слово языка. Таким образом, в дереве будет $S$ листов, а если его строить сбалансированным (так, что расстояние до каждого листа одно и то же), то его глубина будет $\log_2 S$.

Ниже приведён пример такого дерева:

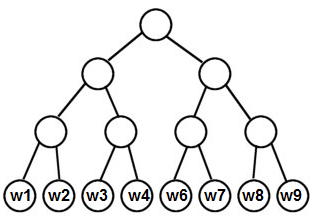
Вместо выходных эмбеддингов каждого слова $\{v_w\}_w$ вычисляются выходные эмбеддинги $\{v_j\}_j$ для каждого внутреннего узла $j$ бинарного дерева.

Пусть нам нужно посчитать вероятность $p(w_O|w_I)$. Эту вероятность можно посчитать не за $O(S)$, а за $O(\log S)$, осуществляя спуск по бинарному дереву от корня до предсказываемого слова $w_O$.

Вероятность из каждого узла $j$ перейти в левого и правого потомка задаётся как

$$\begin{align*} p(\text{left}|j) &= \sigma\left(v_{j}^{T}u_{w_I}\right),\\ p(\text{right}|j) &= 1-\sigma\left(v_{j}^{T}u_{w_I}\right)=\sigma\left(-v_{j}^{T}u_{w_I}\right), \end{align*}$$

где $\sigma(\cdot)$ - сигмоидная функция.

а целевая вероятность $p(w_O|w_I)$ считается как произведение этих вероятностей при спуске от корня до слова $w_O$.

После настройки Skip-Gram этим методом в конечном итоге используются входные эмбеддинги слов $\{u_w\}_w$, поскольку выходные эмбеддинги соответствуют не словам, а узлам дерева.

Дополнительное ускорение

Метод Hierarchical SoftMax можно дополнительно ускорить, строя не сбалансированное дерево, а несбалансированное дерево Хаффмана, которое более частым словам будет назначать более короткие пути на дереве от корня до соответствующего листа.

Негативное сэмплирование

Метод негативного сэмплирования (negative sampling) представляет собой альтернативный подход к настройке Skip-Gram модели. В нём для известного слова $w_t$ и предсказываемого $w_{t+i}$ максимизируется не логарифм вероятности $p(w_{t+i}|w_t)$, а минимизируется другая суррогатная, зато быстро вычислимая функция.

Как и раньше, мы сканируем текст скользящим окном. Для каждого положения окна и известного слова $w_t$ в его центре, а также для предсказываемого соседнего слова $w_{t+i}$ сэмплируется $D$ случайных слов $w_{j(1)},w_{j(2)},...w_{j(D)}$, после чего производится одна итерация оптимизационного алгоритма, максимизирующего следующий критерий:

$$\ln\underset{\sigma\left(\mathbin{\color{red}+}u_{w_{t}}^{T}v_{w_{t+i}}\right)}{\underbrace{\left(\frac{1}{1+e^{\mathbin{\color{red}-}u_{w_{t}}^{T}v_{w_{t+i}}}}\right)}}+\sum_{k=1}^{K}\ln\underset{\sigma\left(\mathbin{\color{red}-}u_{w_{t}}^{T}v_{w_{t+i}}\right)}{\underbrace{\left(\frac{1}{1+e^{\mathbin{\color{red}+}u_{w_{t}}^{T}v_{w_{t+i}}}}\right)}}\to\text{max}_{u_{w_{t}},v_{w_{t+i}}}$$

Первое слагаемое сближает эмбеддинги слов, которые являются соседями, а второе - раздвигает эмбеддинги выбранного слова и случайных слов, которые (в общем случае) не попали в его контекст.

Случайные слова можно сэмплировать из априорного распределения:

$$w\sim p(w),$$

то есть из вероятности встречи каждого слова в тексте самого по себе. Однако метод работает эффективнее, когда чаще сэмплируются более редкие слова, что достигается сэмплированием $p\left(w_{j(k)}\right)\propto p(w)^{3/4}$. Гиперпараметр $D$ берётся из диапазона 2-5.

Метод негативного сэмплирования является более распространённым, чем иерархический SoftMax, поскольку одна его итерация работает за $O(K)$, а не за $O(\log S)$, а $K$ можно выбрать небольшим (рекомендуется порядка 2-20). При этом оба метода обеспечивают примерно одинаковое качество итоговых эмбеддингов.

Литература

1. Mikolov T. et al. Distributed representations of words and phrases and their compositionality //Advances in neural information processing systems. – 2013. – Т. 26.