Моделирующие способности нейросети

Двухслойный персептрон

Сколько слоёв достаточно для моделирования произвольной регрессионной или классификационной зависимости? Теоретические результаты в статьях [1-4] показывают, что двухслойная нейросеть является универсальным аппроксиматором, то есть способна приблизить любую регулярную зависимость для широкого класса функций активации, включая все изученные, кроме тождественной.

В частности, в статье [2] доказывается теорема:

Теорема (Цыбенко, 1989): для любой непрерывной функции $f(\mathbf{x}): \mathbb{R}^m \to \mathbb{R}$ и для любого $\varepsilon>0$ найдётся число $N$, вектора $\mathbf{w}_1,...\mathbf{w}_N$ и числа $b_1,...b_N$, $\alpha_1,...\alpha_N$, для которых

$$\left| f(\mathbf{x})-\sum_{i=1}^N\alpha_i\sigma(\mathbf{x}^T w_i+b_i)\right|<\varepsilon$$

для любых объектов $\mathbf{x}$ из единичного куба: $0 \le x^1\le 1, 0 \le x^2\le 1, ... 0 \le x^D\le 1$.

Таким образом, двухслойной сети с сигмоидными функциями активации достаточно, чтобы с любой заданной точностью моделировать любую непрерывную функцию в ограниченной (компактной) области. Аналогичные утверждения справедливы и для других изученных нелинейных функций активации.

В этом можно убедиться на практике, моделируя, например, следующую целевую функцию:

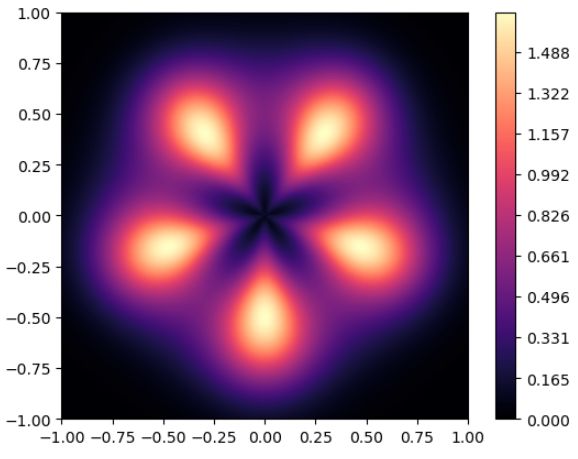
Попробуем её приближать с помощью двухслойного персептрона c $K$ нейронами на скрытом слое, использующим активации LeakyReLU:

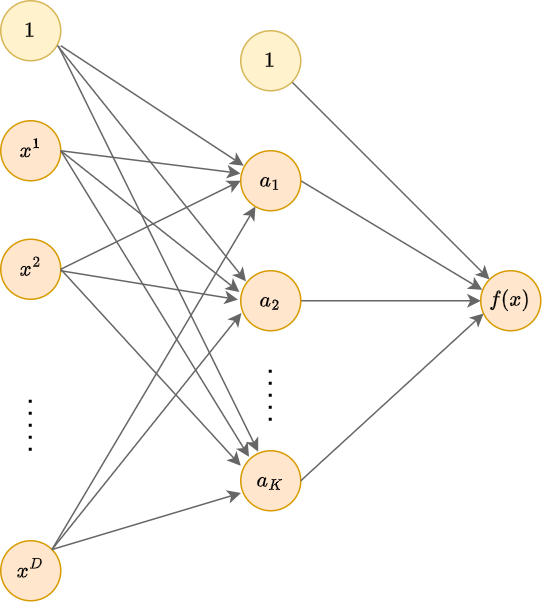
При $K=5$ (у модели будет 21 параметр) получаем не очень точную аппроксимацию:

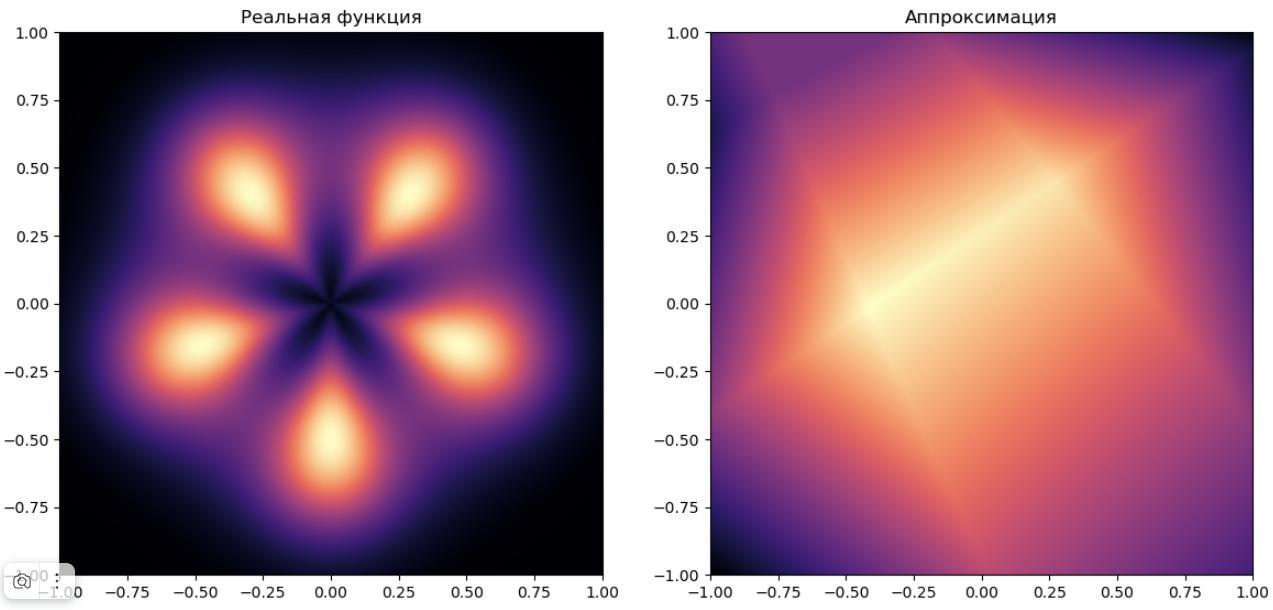
При K=50 (у модели уже 201 параметр) качество аппроксимации вырастает:

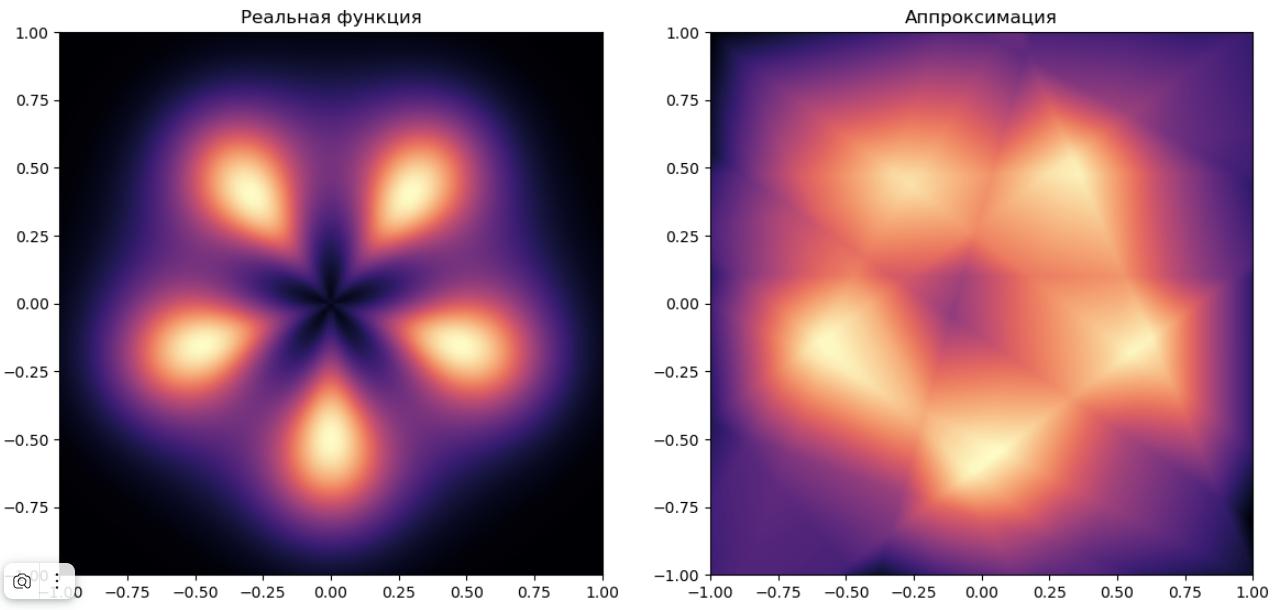
При $K=15000$ (60001 параметр) получим очень высокое качество:

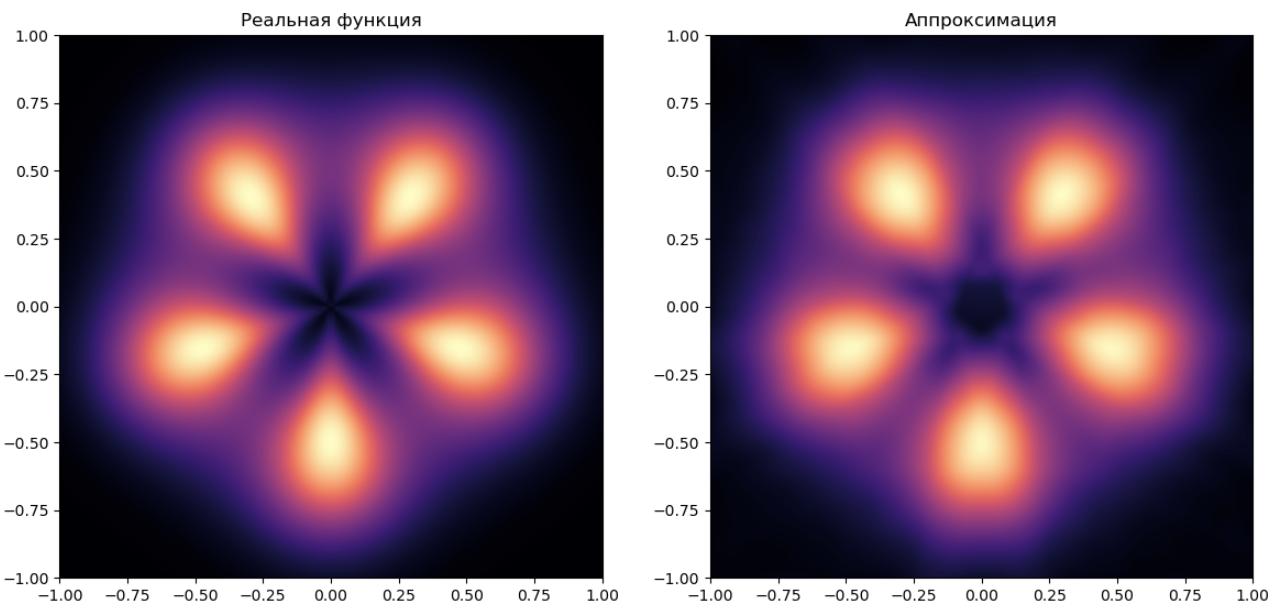
Оно всё же пока неидеальное (см. аппроксимацию чёрной звезды в центре изображения), но может и дальше улучшаться за счёт дальнейшего повышения числа нейронов в скрытом слое $K$.

Глубокие нейросети

Применим принцип глубокого обучения, когда признаки автоматически настраиваются для итоговой прогностической модели. Для этого применим 5-слойный персептрон с 360, 80, 20, 5, 1 нейронами на слоях и активациями LeakyReLU (кроме выходного слоя с тождественной активацией).

Получим ещё более качественную аппроксимацию:

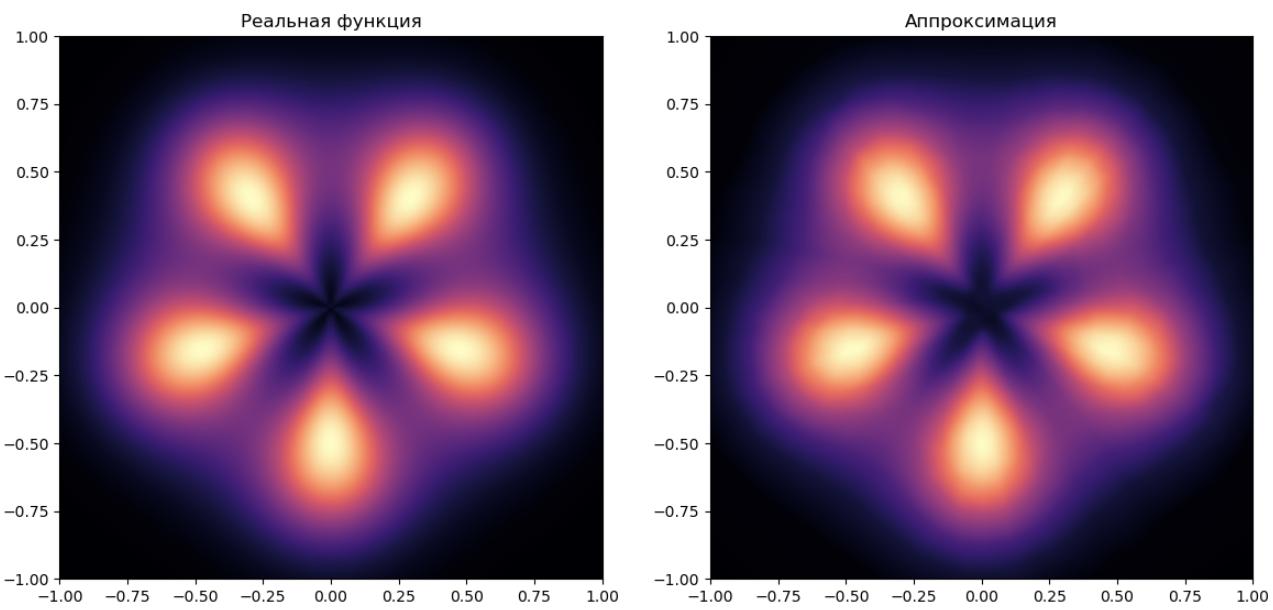
Визуально видно, что чёрная звезда в центре аппроксимируется лучше.

По формальным критериям (RMSE) качество выросло более, чем в 3 раза, при этом в модели настраивался всего 31691 параметр - почти в 2 раза меньше, чем в двухслойном персептроне с максимальным числом нейронов!

Это объясняется тем, что если неглубокой сети приходилось генерировать много простых признаков (грубо говоря, выделяющих полуплоскости), то в глубокой сети признаки получаются более сложными, за счёт чего исходную функцию удалось качественно приблизить меньшим числом таких признаков. Также в неглубокой сети простые признаки комбинировались лишь линейно, в то время как в глубокой сети высокоуровневые признаки нелинейно переиспользовались много раз. Это позволило описать сложную закономерность более экономично с меньшим числом параметров!

Извлечение сложных высокоуровневых признаков, позволяющих компактно описать сложные зависимости в данных, называется обучением представлений (representation learning).

Построение архитектуры, выделяющей качественные промежуточные представления для решения смежных задач, представляет собой отдельное направление исследований.

Литература

1. Funahashi, K. 1989. “On the approximate realization of continuous mappings by neural networks.” Neural Networks 2 (3): 183–192.

2. Cybenko, G. 1989. “Approximation by superpositions of a sigmoidal function.” Mathematics of Control, Signals and Systems 2:304–314.

3. Hornik, K., M. Stinchcombe, and H. White. 1989. “Multilayer feedforward networks are universal approximators.” Neural Networks 2 (5):359–366.

4. Leshno, M., V. Y. Lin, A. Pinkus, and S. Schocken. “Multilayer feedforward networks with a nonpolynomial activation function can approximate any function.” Neural Networks 6:861–867.