Модель нейрона

Нейронные сети (neural networks) изначально появились как попытка моделировать работу человеческого мозга, который состоит из нейронов, связанные друг с другом аксонами - вытянутыми отростками нервных клеток. Каждый нейрон может перейти в возбуждённое состояние, в этом случае он передаёт по аксонам сигнал другим нейронам посредством электро-химического взаимодействия.

Нейрон (neuron) моделируется следующим преобразованием:

$$a=h\left( \sum_{k=0}^K w_{k} a_k \right),$$

где

• $a$ - выход нейрона (что он посылает по аксонам другим нейронам);

• $a_0\equiv 1$ - нейрон, всегда выдающий константу 1;

• $a_1,...a_K$ - нейроны, имеющие входящую связь с рассматриваемым нейроном;

• $w_0,w_1,...w_K$ - веса связей;

  • они показывают, во сколько раз изменяется сигнал, передаваемый нейронами $a_0,a_1,...a_K$ текущему нейрону $a$;

• $h(\cdot)$ - некоторая фиксированная функция активации (activation function).

Геометрически это можно представить следующим образом:

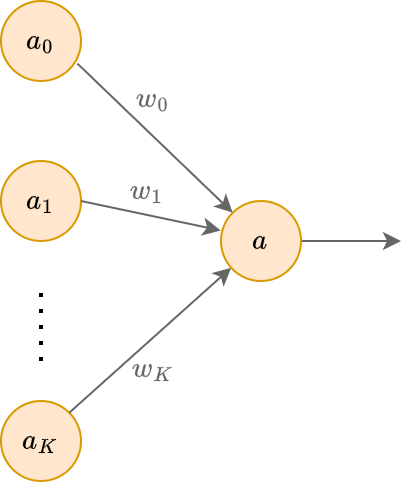
Модель нейрона в машинном обучении

В машинном обучении нейрон можно применять как прогнозирующую модель. Тогда вместо активаций нейронов предыдущего слоя на вход нейрону подаваться исходные признаки, а также константа 1:

$$a_0\equiv 1,\,a_1=x^1,\,a_2=x^2\,...a_{K}=x^D$$

Напомним, что в учебнике признаки обозначаются верхним индексом: $x^i$ - $i$-й признак вектора признаков. А $\mathbf{x}_n$ - $n$-й объект обучающей выборки.

Одиночный нейрон будет моделировать закономерность:

$$y(\mathbf{x})=h\left( w_{0} + \sum_{d=1}^D w_{d} x^d \right),$$

где параметр $w_0$ называется смещением (bias).

Веса $w_0,w_1,...w_{D}$ представляют собой параметры, настраиваемые по данным. В зависимости от того, как выбрать функцию активации, мы сможем решать как задачу регрессии, так и задачу бинарной классификации.

Регрессия

Регрессия получается при выборе $h(u)=u$. Тогда

$$y(\mathbf{x}) = w_{0} + \sum_{d=1}^D w_{d} x^d$$

Бинарная классификация

Классификация получается при выборе сигмоидной функции активации:

$$h(u)=\sigma(u)=1/(1+e^{-u})$$

Эта функция принимает значения на интервале $(0,1)$, поэтому её можно трактовать как вероятность положительного класса:

$$p(y=+1|\mathbf{x})=\sigma\left( w_{0} + \sum_{d=1}^D w_{d} x^d \right)$$

Тогда вероятность отрицательного класса можно посчитать как

$$p(y=-1|\mathbf{x}) = 1 - p(y=+1|\mathbf{x})$$

Это даёт нам нейросетевую реализацию бинарной логистической регрессии.