Симметрия в пространстве весов

Рассмотрим пример многослойного персептрона:

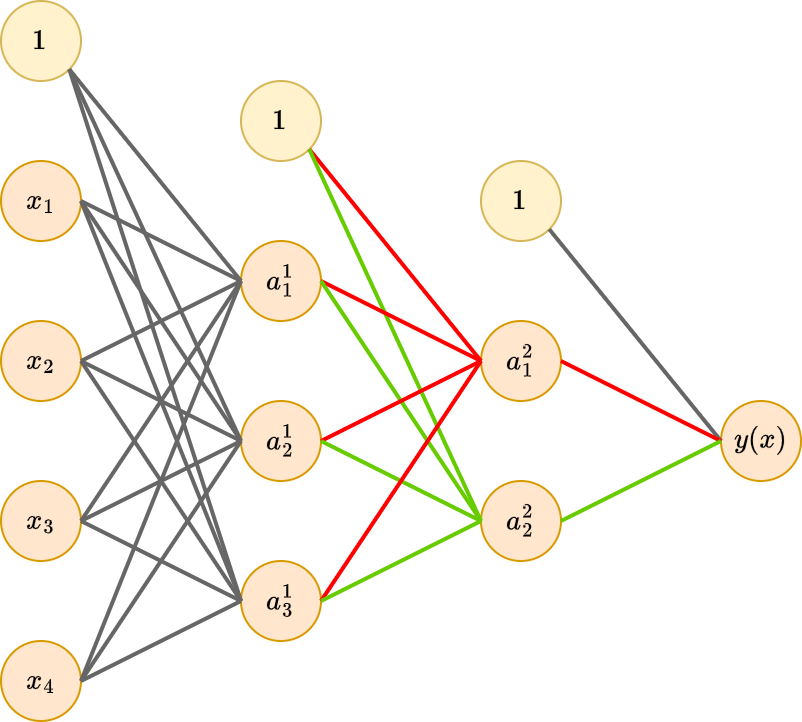
Нетрудно заметить, что если синхронно переставить веса для всех входящих и исходящих связей для любой пары нейронов некоторого скрытого слоя, то мы получим нейросеть, моделирующую в точности ту же самую закономерность!

Например, на рисунке можно синхронно поменять местами связи, выделенные красным и зелёным цветом - получим эквивалентную нейросеть!

Если в слое $M$ нейронов, сколько эквивалентных перестановок такого типа можно произвести?

$M!=M \cdot (M-1) \cdot (M-2) \cdot ... \cdot 2 \cdot 1$ перестановок.

Если всего есть K скрытых слоёв с числом нейронов $M_1,M_2,...M_K$, то сколько всего эквивалентных перестановок можно произвести, получая ту же самую функцию?

Поскольку мы можем переставлять нейроны в рамках каждого слоя независимо, то всего будет $M_1! \cdot M_2! \cdot ... \cdot M_{K-1}! \cdot M_K!$ перестановок.

Если используются нечётные функции активации (т.е. для которых $h(-u)=-h(u)$), то, выбрав какой-то нейрон, можно синхронно изменять знак входящих и исходящих связей - это также не окажет влияния на итоговую зависимость.

Какие из рассмотренных функций активации являются нечётными?

Тождественная, гиперболический тангенс, SoftSign и жёсткий гиперболический тангенс.

Указанные симметрии в пространстве весов показывают, что функция потерь в пространстве весов будет обладать не одним, а большим количеством эквивалентных минимумов, за счёт чего, в частности, она является невыпуклой.

На практике это не имеет большого значения, поскольку из всего многообразия эквивалентных минимумов функции потерь нам достаточно найти хотя бы один.