Обобщающая способность модели

После настройки параметров модели на обучающей выборке (training set) $[X,Y]$, нам бы хотелось оценить, насколько хорошо она будет работать на новых данных - тестовой выборке (test set) $[X',Y']$, т.е. оценить так называемую обобщающую способность (generalization ability) - способность модели успешно экстраполировать выученные зависимости при обучении. Ведь именно для этого мы и настраивали модель!

Тут важно помнить, что эмпирический риск на обучающей выборке не будет репрезентативно отражать эмпирический риск на новых данных, и в общем случае мы будем наблюдать, что $L(\hat{\mathbf{w}}|X,Y)<L(\hat{\mathbf{w}}|X',Y')$, поскольку $\hat{\mathbf{w}}$ выбиралась так, чтобы минимизировать ошибки именно на обучающих данных $(X,Y)$, но не новых. Мы лишь надеемся, что новые данные будут распределены примерно так же, как в обучающей выборке.

Чем более сложная (гибкая, с большим числом параметров) у нас модель, тем легче ей подстроиться под обучающую выборку и тем меньше будет $L(\hat{\mathbf{w}}|X,Y)$, однако это далеко не всегда будет приводить к снижению $L(\hat{\mathbf{w}}|X',Y')$! Например, мы решаем задачу линейной регрессии по одномерному признаку $x$ и отклику $y$. Управлять сложностью получаемой модели можно за счет поиска линейной зависимости не только от $x$, но и от квадрата признака $(x)^2$, куба признака $(x)^3$ и так далее до определённой степени $(x)^K$. Тогда наша модель будет иметь вид:

$$\hat{y}=w_0+w_1 x+w_2 (x)^2+...+w_K (x)^K,$$

и будет моделировать множество всевозможных полиномиальных зависимостей $y$ от $x$. Выбирая различные $K$, мы будем управлять сложностью получаемой модели. На рисунке ниже обучающая выборка в осях $x,y$ показана точками, а прогнозы модели при различных $K$ показаны пунктирной линией. Видно, что малое $K=1$ (слева) будет приводить к линейной зависимости, которая слишком проста для реальной зависимости в данных, что соответствует недообученной модели (underfitted model), в то время как при высоком $K$ (справа) зависимость получается сложнее реальной зависимости и приводит к переобученной модели (overfitted model). Промежуточное $K$ приводит к модели, сложность которой примерно соответствует сложности реальных данных.

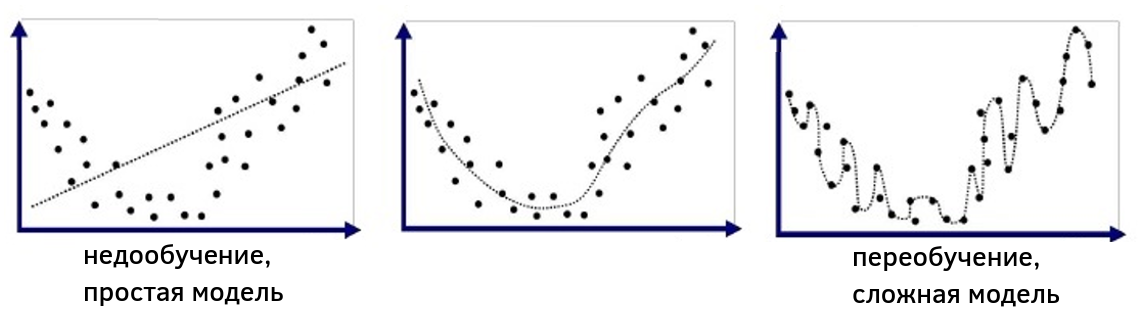
Более формально понятия недообученных и переобученных моделей будут рассмотрены в отдельном разделе учебника.

Гиперпараметры моделей

Такой параметр, как $K$ в примере, который не настраивается на обучающей выборке (как вектор весов $\mathbf{w}$), а выбирается пользователем, называется гиперпараметром (hyperparameter).

Подумайте, почему K нельзя настраивать на обучающей выборке?

Такой способ настройки будет всегда поощрять более гибкую модель с большим значением K.

В частности, при K>=N-1 модель будет иметь как минимум столько же настраиваемых параметров, сколько объектов в выборке, и сможет обеспечить безошибочные прогнозы на всех объектах обучающей выборки, но не на новых тестовых объектах!

У большинства моделей машинного обучения есть гиперпараметр, отвечающий за сложность модели. Важно тщательно настроить этот гиперпараметр, чтобы сложность модели соответствовала сложности реальной зависимости в данных.

Если модель будет слишком простой, то она будет показывать недостаточную точность из-за того, что у неё не хватает выразительной способности описать реальную зависимость.

Если же модель будет слишком сложной, то она начнёт перенастраиваться на особенности реализации обучающей выборки (которая случайна в силу случайного отбора объектов в неё) вместо подгонки под реальную зависимость, что также негативно повлияет на её обобщающую способность на тестовых данных. Детальнее недообученные и переобученные модели будут описаны в отдельном разделе книги.

Вы также можете прочитать недообученных и переобученных моделях в [1].

Литература

1. Geeksforgeeks: underfitting and overfitting.