Выпуклость потерь

В машинном обучении приветствуется выбор выпуклых функций потерь (convex loss functions) от параметров (или весов) модели, т.е. таких функций, что

$$L(a*\mathbf{w}+(1-a)\mathbf{w}')\le aL(\mathbf{w})+(1-a)L(\mathbf{w}')\quad \forall \mathbf{w},\mathbf{w}'\text{ и } a\in[0,1].$$

Также такие функции называются выпуклыми вверх (функции, выпуклые вниз, называются вогнутыми, и для них выполнено неравенство в обратную сторону).

Неравенство выполнено для любых аргументов $\mathbf{w},\mathbf{w}'$ из области определения функции, которое также должно быть выпуклым (т.е. если две точки принадлежат области определения, то и любая промежуточная точка на отрезке, их соединяющем, тоже принадлежит области определения функции). Геометрически определение выпуклой функции означает, что отрезок, соединяющий любые две точки на функции, нигде не может лежать выше значений функции.

Пример выпуклой функции от одной переменной показан ниже:

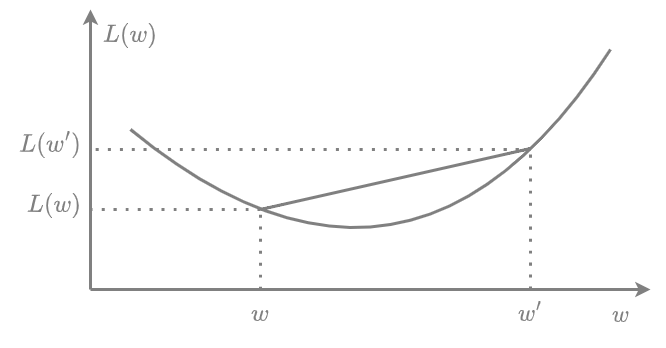
Стоит отметить, что если потери на отдельном объекте $\mathcal{L}(f_{\mathbf{w}}(\mathbf{x}_{n}),y_{n})$ выпуклы по $\mathbf{w}$, то и потери по всей обучающей выборке (эмпирический риск) будут выпуклыми, т.к. усреднение выпуклых функций всегда будет тоже выпуклой функцией (докажите!).

Выпуклые функции удобны тем, что

• любой локальный минимум является глобальным;
• равенство нулю производной является не только необходимым, но и достаточным условием минимума.

Таким образом, найдя значение $\hat{\mathbf{w}}$, в котором $\nabla L(\hat{\mathbf{w}})=0$, мы точно знаем, что это глобальный минимум.

Основные функции потерь машинного обучения для задач регрессии и классификации выпуклы.

Задача

Попробуйте доказать эти свойства. Для доказательства второго свойства пригодится использование другого критерия выпуклой функции, что она всегда лежит не ниже касательной, проведённой в любой точке.

Может ли у выпуклой функции не быть минимума?

Да, рассмотрите функцию $y=1/x$.

Может ли у выпуклой функции быть несколько минимумов?

Да, рассмотрите функцию $y=\max\{0,\vert x \vert-1\}$.