DBSCAN

Рассмотренные ранее методы ищут кластеры сферической или эллиптической формы и требуют заранее задать число кластеров $K$. Однако в реальных данных кластеры могут иметь сложную геометрическую структуру (например, вложенные кольца, ленточные структуры произвольной формы) и содержать шум.

Для решения таких задач разработан алгоритм DBSCAN (Density-Based Spatial Clustering of Applications with Noise [1]).

В предположении алгоритма кластеры — это области высокой плотности точек, разделенные областями низкой плотности. Точки в областях низкой плотности считаются шумом (выбросами). Алгоритм использует локальные плотностные характеристики точек данных для их объединения в кластеры.

Основные определения

Плотность в точке определяется количеством соседей, попадающих в радиус $\varepsilon$ (включая саму точку). Алгоритм опирается на два гиперпараметра:

1. $\varepsilon$ — радиус окрестности.
2. $M$ — минимальное количество точек в окрестности для того, чтобы считать область плотной.

Все точки классифицируются на три типа:

1. Ядровая точка (core point): Точка объявляется ядровой, если в её $\varepsilon$-окрестности находится не менее $M$ точек.

2. Граничная точка (border point): Точка объявляется граничной, если в её $\varepsilon$-окрестности находится меньше $M$ точек, но она содержит в своей окрестности хотя бы одну ядровую точку.

3. Шумовая точка (noise point): Точка, которая не является ни ядровой, ни граничной.

Ниже проиллюстрированы точки A, B и C, которые являются ядровой, граничной и шумовой соответственно при $M=10$:

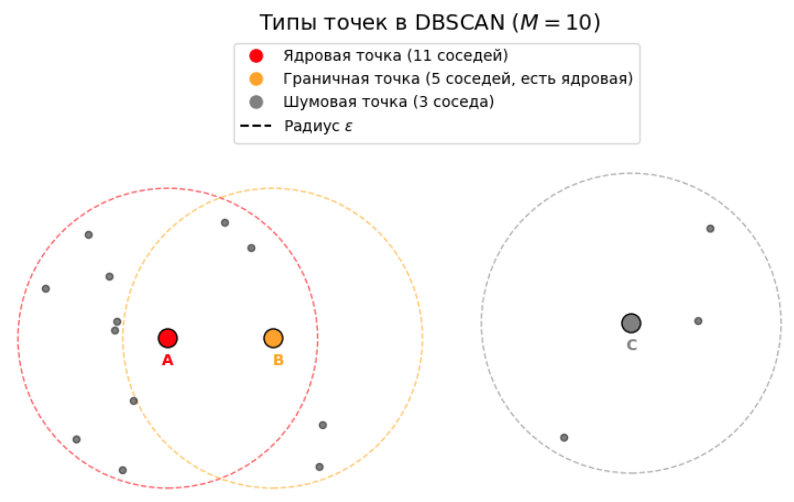
Алгоритм DBSCAN

Логика работы DBSCAN отличается от итеративного пересчета центров. Кластеризация выполняется следующим образом:

1. Определение типов точек: Для всего датасета определяются ядровые, граничные и шумовые точки при заданных параметрах $(\varepsilon, M)$.

2. Построение графа ядровых точек: Создается граф, вершинами которого являются только ядровые точки. Ребро между двумя ядровыми точками добавляется тогда и только тогда, когда расстояние между ними не превышает $\varepsilon$.

3. Поиск компонент связности: В этом графе находятся все связные компоненты. Каждая связная компонента и является искомым кластером.

4. Привязка граничных точек: Каждая граничная точка приписывается к той компоненте связности (кластеру), с которой она лучше всего связана (находится в $\varepsilon$-окрестности ядровой точки этого кластера).

5. Формирование результата: Точки каждой компоненты вместе с приписанными граничными точками возвращаются как кластеры. Шумовые точки помечаются как выбросы.

В отличие от центроидных методов (K-means), которые тяготеют к выпуклым (сферическим) кластерам, DBSCAN корректно выделяет кластеры любой геометрической формы. Ниже показано сравнение кластеризации методом K-средних и DBSCAN:

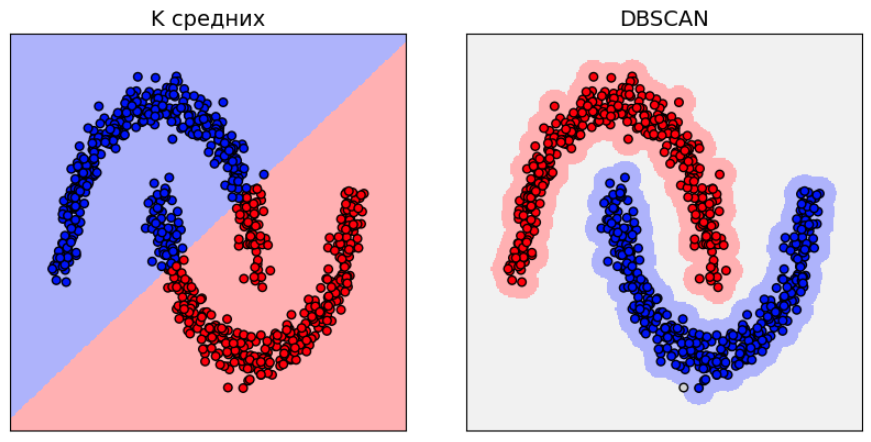
Обратим внимание, что за пределами небольшой окрестности кластеров точки в DBSCAN будут относиться к шуму, поэтому большая часть признакового пространства не закрашена.

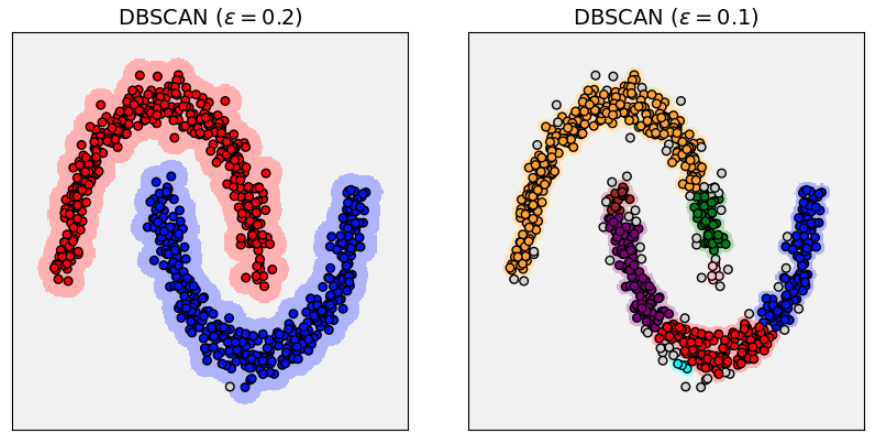
При уменьшении $\varepsilon$ будет возрастать число точек, отнесённых к шуму:

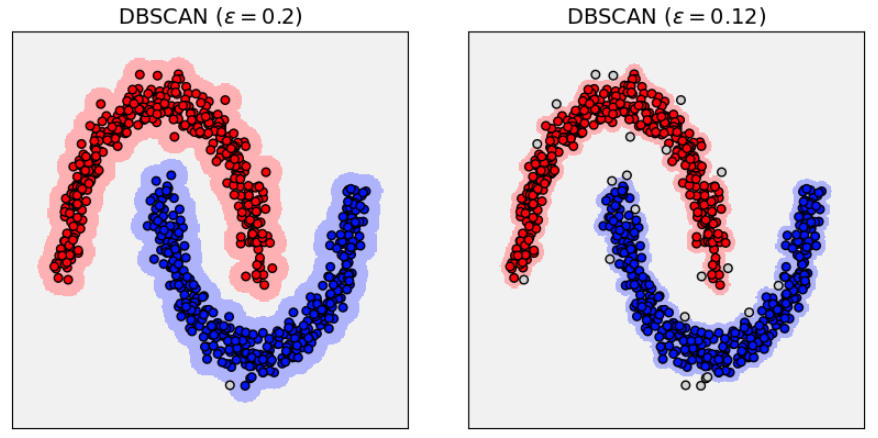
Формально алгоритм самостоятельно определяет число кластеров. Однако фактическое число кластеров будет зависеть от выбора гиперпараметров $M$ и $\varepsilon$.

При слишком большом $\varepsilon$ группы объектов будут сливаться в один кластер:

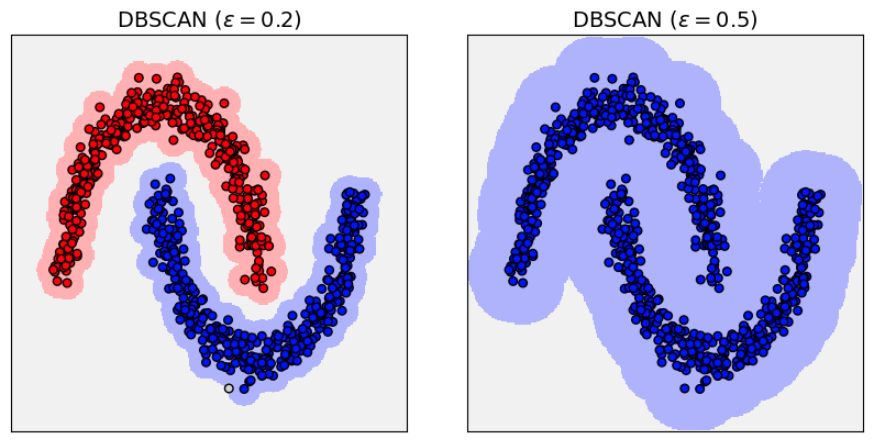
А при слишком малом $\varepsilon$ группы будут разбиваться на более мелкие кластера за счёт небольших вариаций в плотности точек в рамках каждой группы:

Выбор гиперпараметров

В оригинальной статье [1] предлагается выбрать $M$ небольшой константой (тем выше, чем выше априорные ожидания об уровне шума в данных), а гиперпараметр $\varepsilon$ предлагается выбрать следующим образом:

1. Для каждой точки $\mathbf{x}$ из датасета вычисляется расстояние до её $M$-го ближайшего соседа.

2. Полученные значения расстояний сортируются по убыванию.

3. Строится график, где по оси X откладывается индекс точки в отсортированном списке, а по оси Y — значение расстояния.

4. На графике визуально определяется точка максимального перегиба («локтя» или «колена»). Значение расстояния по оси Y в этой точке принимается в качестве $\varepsilon$.

Логика метода основывается на том, что внутри плотного кластера расстояние до $M$-го соседа для большинства точек будет небольшим и примерно одинаковым (формируя пологую часть графика, "плато").

Напротив, для шумовых точек и выбросов, находящихся в разреженных областях, $M$-й сосед будет находиться значительно дальше, что даст резкий скачок значений на графике (крутая часть слева).

Точка перегиба является порогом, разделяющим эти два режима: выбрав $\varepsilon$ на уровне этого излома, мы классифицируем точки с аномально большими расстояниями как шум, а остальные — как кандидатов в ядровые или граничные точки.

Проблема переменной плотности

Алгоритм DBSCAN использует глобальный параметр $\varepsilon$, что затрудняет выделение этим методом кластеров переменной плотности. Рассмотрим, например, следующий пример данных:

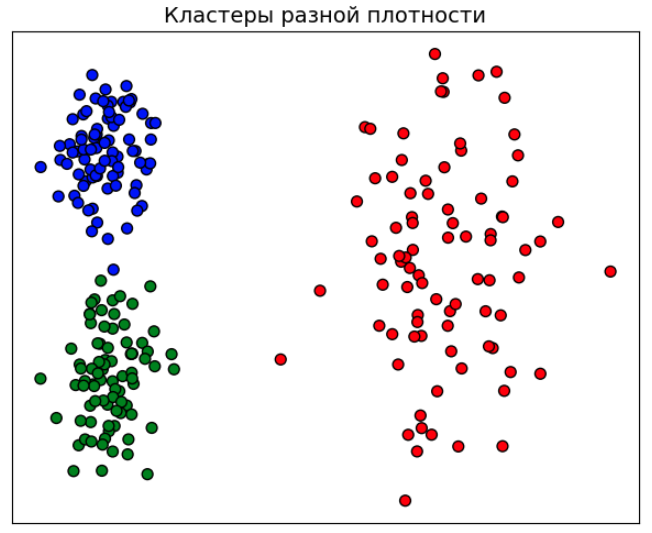
Если выбрать $\varepsilon$ слишком большим, то зелёный и синий кластера сольются в один кластер. Если же выбрать $\varepsilon$ слишком малым, то почти все точки красного более разреженного кластера будут отнесены к шуму.

Литература

1. Ester M. et al. A density-based algorithm for discovering clusters in large spatial databases with noise //kdd. – 1996. – Т. 96. – №. 34. – С. 226-231.