Вариации метода K представителей

Общая схема алгоритма $K$ представителей позволяет гибко настраивать метод под природу данных, изменяя функцию расстояния $\rho(\boldsymbol{x}, \boldsymbol{\mu})$ и способ обновления центров. Рассмотрим наиболее важные частные случаи помимо метода K-средних.

Метод K-медиан (K-medians)

Этот метод получается, если вместо квадратичного Евклидова расстояния использовать Манхэттенское расстояние ($L_1$-норму).

Спецификация

Функция потерь для одного объекта:

$$\rho(\boldsymbol{x}, \boldsymbol{\mu}) = \|\boldsymbol{x} - \boldsymbol{\mu}\|_1 = \sum_{j=1}^D |x^j - \mu^j|$$

Глобальный функционал ошибки (инерция):

$$\mathcal{L} = \sum_{n=1}^{N} \sum_{j=1}^D |x_n^j - \mu_{z_n}^j| \to \min_{\boldsymbol{z}, \boldsymbol{\mu}}$$

Обновление центров

На шаге пересчета центров нам необходимо найти вектор $\boldsymbol{\mu}_k$, минимизирующий сумму модулей отклонений для объектов кластера $C_k$:

$$\boldsymbol{\mu}_k = \arg\min_{\boldsymbol{\mu}} \sum_{n \in C_k} \sum_{j=1}^D |x_n^j - \mu^j|$$

Поскольку слагаемые по разным измерениям $j$ независимы, задачу можно решать для каждого признака отдельно. Известно, что сумма модулей разностей $|a - c|$ минимизируется, когда $c$ является медианой выборки $a$.

Следовательно, новый центр кластера вычисляется как покомпонентная медиана:

$$\mu_k^j = \text{median}(\{x_n^j \mid n \in C_k\})$$

Особенности метода

• Форма кластеров: Использование $L_1$-метрики приводит к тому, что линии уровня имеют форму гипероктаэдров (ромбов в 2D). Кластеры стремятся выравниваться вдоль осей координат.
• Устойчивость к выбросам: Это главное преимущество метода. Квадратичная функция в K-means сильно штрафует большие отклонения, поэтому один далекий выброс может сильно сместить среднее значение. Медиана же устойчива к отдельным аномальным значениям.

Сравнение среднего и медианы

Пусть кластер состоит из точек $\{1, 2, 3, 100\}$.

• Среднее (K-means): $(1+2+3+100)/4 = 26.5$. Центр смещен в сторону выброса, далеко от основной массы наблюдений.
• Медиана (K-medians): $2.5$. Центр находится внутри плотной группы, игнорируя выброс $100$.

Финансы и экономика: Выбросы часто возникают при анализе, например, финансовых данных, таких как доходы населения. Среднее значение в таких случаях становится слабо репрезентативным.

Кластеризация с расстоянием Махаланобиса

Классический метод K-средних строит сферические кластеры, так как использует Евклидово расстояние. Если данные вытянуты в эллипсоиды (есть корреляция между признаками) или имеют разный масштаб, K-средних может работать некорректно, разбивая один вытянутый кластер на части.

Решение состоит в использовании в методе K-представителей в качестве функции расстояния не квадрата Евклидовой, а квадрата расстояния Махаланобиса:

$$\rho(\boldsymbol{x}, \boldsymbol{\mu}_k) = (\boldsymbol{x} - \boldsymbol{\mu}_k)^T \boldsymbol{\Sigma}_k^{-1} (\boldsymbol{x} - \boldsymbol{\mu}_k),$$

где $\boldsymbol{\Sigma}_k$ - ковариационная матрица объектов, попавших в $k$-й кластер, позволяющая учитывать эллипсоидальную форму кластера.

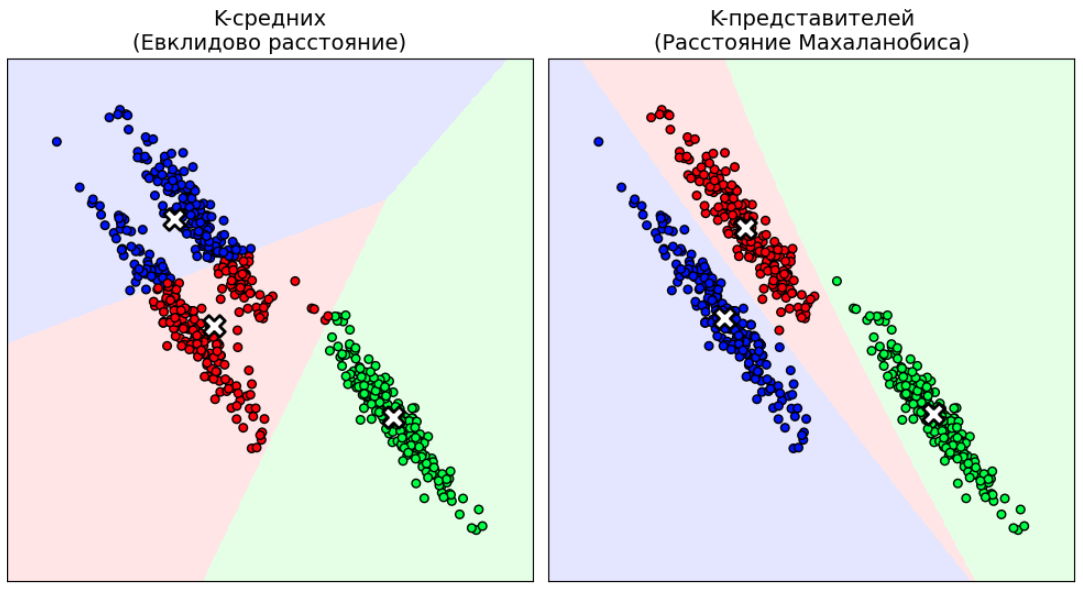
Сравнение разбиения кластеров эллипсоидальной формы с помощью K-средних и K-представителей с расстоянием Махаланобиса приведён ниже:

Обновление параметров

В этом методе, помимо центров $\boldsymbol{\mu}_k$, на каждом шаге необходимо обновлять и матрицы ковариации $\boldsymbol{\Sigma}_k$ для каждого кластера.

1. Центры: Как и в K-means, остаются средними арифметическими:

   $$\boldsymbol{\mu}_k = \frac{1}{|C_k|} \sum_{n \in C_k} \boldsymbol{x}_n$$

2. Ковариационные матрицы: Вычисляются как выборочная ковариация точек кластера:

   $$\boldsymbol{\Sigma}_k = \frac{1}{|C_k|} \sum_{n \in C_k} (\boldsymbol{x}_n - \boldsymbol{\mu}_k)(\boldsymbol{x}_n - \boldsymbol{\mu}_k)^T$$

Особенности метода

• Адаптивность формы: Метод способен выделять кластеры эллиптической формы, причем эллипсы могут быть повернуты и иметь разный размер для разных кластеров.
• Инвариантность: Результат не зависит от линейных преобразований координат - масштабирования и поворота.
• Связь с GMM: Данный подход с точностью до сдвига эквивалентен алгоритму кластеризации смесью Гауссиан (Gaussian Mixture Models, GMM) при сопоставлении каждому объекту одного кластера.

Вычислительная сложность

Необходимость хранить и обращать матрицу $\boldsymbol{\Sigma}_k$ размера $D \times D$ на каждой итерации делает метод вычислительно дорогим ($O(D^3)$). Кроме того, для корректной оценки ковариации требуется много данных ($|C_k| > D$), иначе матрица может стать вырожденной.

Этот метод удобен для кластеризации разнородных данных, в которых признаки имеют разную природу и масштаб, когда мы не хотим подбирать коэффициенты нормализации вручную.

Метод K-медоидов (K-medoids)

Методы К-средних и K-представителей с расстоянием Махаланобиса основаны на итеративном уточнении центроидов кластеров $\boldsymbol{\mu}_1,...\boldsymbol{\mu}_K$ как выборочных средних по объектам кластера. В случае K-медиан они вычисляются как медианы. Подобная агрегация не возможна, если агрегируются объекты разного размера и структуры, такие как

• временные ряды разной длины;

• изображения разного размера

• графы с разным числом вершин и рёбер.

Даже если объекты представимы в виде векторов одинаковой длины, подобная агрегация не всегда имеет смысл.

Рассмотрим задачу логистики, в которой нужно выбрать $K$ существующих складов из $N$ возможных, чтобы минимизировать время доставки. Мы не можем построить склад в "средней точке" (в чистом поле или озере), мы должны выбрать конкретную локацию.

В таких случаях используется метод K-медоидов, в котором накладывается дополнительное ограничение в том, что центр кластера обязан совпадать с одним из объектов обучающей выборки:

$$\boldsymbol{\mu}_k \in \{\boldsymbol{x}_1, \dots, \boldsymbol{x}_N\}, \quad k=1,2,...K$$

Такой объект-представитель называется медоидом.

При этом функция расстояния $\rho(\boldsymbol{x}, \boldsymbol{x}')$ может быть любой, лишь бы она описывала степень различия между рассматриваемыми объектами.

Обновление центров

На шаге пересчета центров в методе K-представителей для каждого кластера $C_k$ мы ищем такой объект из этого же кластера, который минимизирует суммарное расстояние до остальных:

$$\boldsymbol{\mu}_k = \arg\min_{\boldsymbol{m} \in \{\boldsymbol{x}_n : n \in C_k\}} \sum_{n \in C_k} \rho(\boldsymbol{x}_n, \boldsymbol{m})$$

Здесь требуется для каждого объекта вычислить расстояния до всех остальных объектов его кластера, что делает сложность пересчёта "в лоб" $O(N^2)$ по числу объектов, а не $O(N)$, как в методе K-средних и K-медиан.

Наиболее популярная реализация этого подхода называется PAM (Partitioning Around Medoids).

Особенности метода

• Интерпретируемость: Центр кластера — это реальный пример (например, "типичный покупатель" или "эталонная статья"), а не абстрактный усредненный вектор.
• Универсальность: Работает с любыми типами данных, для которых определена мера близости (строки, множества, временные ряды).
• Устойчивость: Как и K-medians, метод устойчив к выбросам, так как медоид выбирается перебором и не может переместиться в пустое пространство.

Недостатки

Высокая вычислительная сложность. Поиск медоида требует вычисления расстояний "всех со всеми" внутри кластера, что дает квадратичную сложность $O(|C_k|^2)$ на каждой итерации. Существуют улучшенные реализации метода K-представителей для решения задачи K-медоид, такие как алгоритм PAM (Partitioning Around Medoids [1]), FastPAM и FasterPAM [2], но все они всё ещё имеют квадратичную сложность относительно числа объектов.

Поэтому применять метод K-медоид для больших данных можно лишь приближённо, находя примерные расположения медоидов по случайной подвыборке.

Литература

1. Kaufman L. Partitioning around medoids (program pam) //Wiley series in probability and statistics. – 1990. – Т. 344. – С. 68-125.