Метод K-средних

Кластеризация $K$ представителями

Повторим общую схему работы метода $K$ представителей:

1. Инициализировать $\boldsymbol{\mu}_1, \dots, \boldsymbol{\mu}_K$.

2. ПОВТОРЯТЬ до сходимости:

   • Для $n=1,2,...N$ обновить метки кластеров:

     $$z_n=\arg\min_k \rho(\mathbf{x}_n,\boldsymbol{\mu}_k)$$

   • Для $k=1,2,...K$ обновить центроиды кластеров:

     $$\boldsymbol{\mu}_k=\arg\min_{\boldsymbol{\mu}}\sum_{n\in C_k} \rho(\mathbf{x}_n,\boldsymbol{\mu})$$

3. ВЕРНУТЬ $z_1, \dots, z_N$.

Здесь

• $C_k$ индексы объектов, принадлежащих кластеру $k$;

• назначения объектам $\mathbf{x}_1,\mathbf{x}_2,...\mathbf{x}_{N}$ номеров их кластеров $z_{1},...z_{N}$;

• центры каждого кластера $\boldsymbol{\mu}_{1},...\boldsymbol{\mu}_{K}$, называемые также центроидами.

Кластеризация методом $K$ средних

Метод $K$ средних (K-Means) является самым популярным частным случаем общего алгоритма $K$ представителей. Он получается, если в качестве меры расстояния $\rho(\cdot)$ выбрать квадрат Евклидова расстояния:

$$\rho(\boldsymbol{x}, \boldsymbol{\mu}) = \|\boldsymbol{x} - \boldsymbol{\mu}\|^2 = \sum_{j=1}^D (x^j - \mu^j)^2$$

где $\boldsymbol{x} \in \mathbb{R}^D$ — вектор объекта, а $\boldsymbol{\mu} \in \mathbb{R}^D$ — вектор центра кластера. Индекс $j$ здесь обозначает номер признака.

Минимизируемая функция потерь называемая инерцией или внутрикластерной суммой квадратов и выглядит так:

$$\mathcal{L} = \sum_{n=1}^{N} \|\boldsymbol{x}_n - \boldsymbol{\mu}_{z_n}\|^2 \to \min_{\boldsymbol{\mu}, \boldsymbol{z}}$$

Расчёт центроидов

Почему же метод называется "$K$ средних"? Рассмотрим шаг обновления центров при фиксированных метках кластеров $z_1, \dots, z_N$. Нам нужно найти такой вектор $\boldsymbol{\mu}_k$, который минимизирует сумму квадратов расстояний до всех объектов $\boldsymbol{x}_n$, входящих в кластер $C_k$:

$$\boldsymbol{\mu}_k = \arg\min_{\boldsymbol{\mu}} \sum_{n \in C_k} \|\boldsymbol{x}_n - \boldsymbol{\mu}\|^2$$

Функция $J(\boldsymbol{\mu}) = \sum_{n \in C_k} \|\boldsymbol{x}_n - \boldsymbol{\mu}\|^2$ является суммой квадратичных функций, а значит — строго выпуклой (параболоиды с ветвями вверх). Следовательно, условие равенства градиента нулю является не только необходимым, но и достаточным условием глобального минимума.

Возьмем производную по вектору $\boldsymbol{\mu}$ и приравняем её к нулю:

$$\nabla_{\boldsymbol{\mu}} J(\boldsymbol{\mu}) = \sum_{n \in C_k} \nabla_{\boldsymbol{\mu}} (\boldsymbol{x}_n - \boldsymbol{\mu})^T (\boldsymbol{x}_n - \boldsymbol{\mu}) = -2 \sum_{n \in C_k} (\boldsymbol{x}_n - \boldsymbol{\mu}) = 0$$

Раскрывая сумму, получаем:

$$\sum_{n \in C_k} \boldsymbol{x}_n - |C_k| \cdot \boldsymbol{\mu}_k = 0$$

Отсюда следует формула пересчета:

$$\boldsymbol{\mu}_k = \frac{1}{|C_k|} \sum_{n \in C_k} \boldsymbol{x}_n$$

Таким образом, оптимальным представителем кластера по квадрату метрики $L_2$ является среднее арифметическое всех объектов этого кластера.

Алгоритм Ллойда

Классическая реализация метода $K$ средних называется алгоритмом Ллойда. Она выглядит следующим образом:

1. Инициализировать центры $\boldsymbol{\mu}_1, \dots, \boldsymbol{\mu}_K$ (случайно или методом K-means++).

2. ПОВТОРЯТЬ до сходимости:

   • Для $n=1,2,...N$ обновить метки кластеров (Assign step):

     $$z_n = \arg\min_{k \in \{1,\dots,K\}} \|\boldsymbol{x}_n - \boldsymbol{\mu}_k\|^2_2$$

   • Для $k=1,2,...K$ обновить центроиды кластеров (Update step):

     $$\boldsymbol{\mu}_k = \frac{1}{|C_k|} \sum_{n \in C_k} \boldsymbol{x}_n$$

3. ВЕРНУТЬ $z_1, \dots, z_N$.

Инициализация центров

Метод K-средних, как частный случай метода K-представителей, чувствителен к начальной инициализации центров кластеров. К нему применимы те же приёмы повышения эффективности инициализации, что и для метода K-представителей.

Пример работы

Ниже приведен процесс работы алгоритма шаг за шагом:

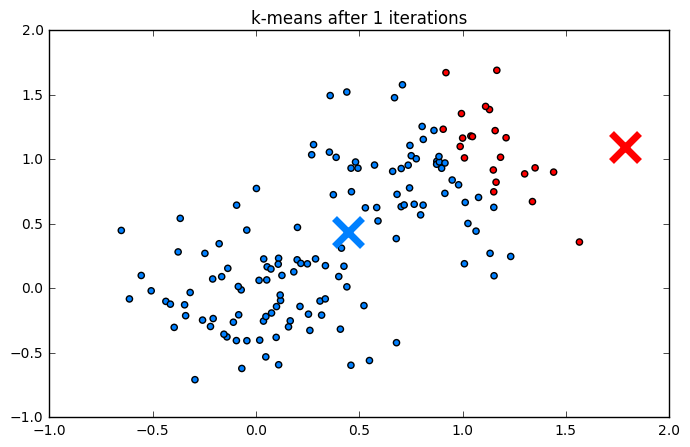
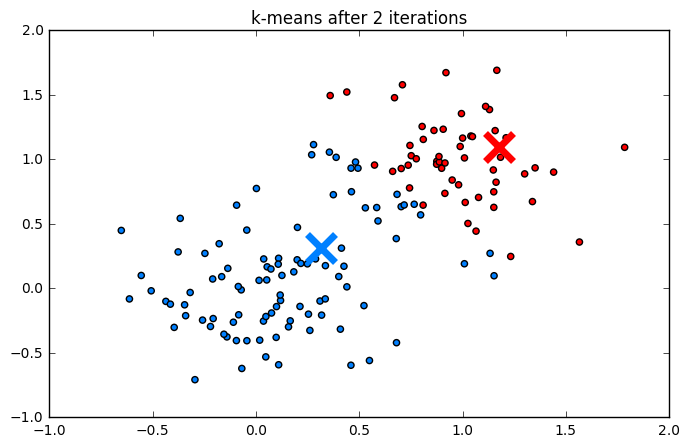
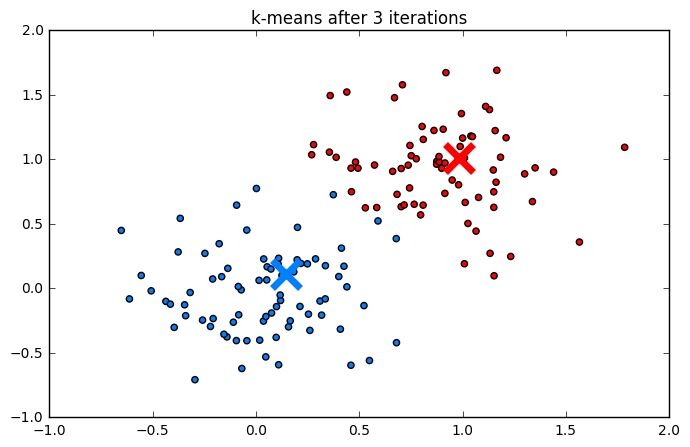
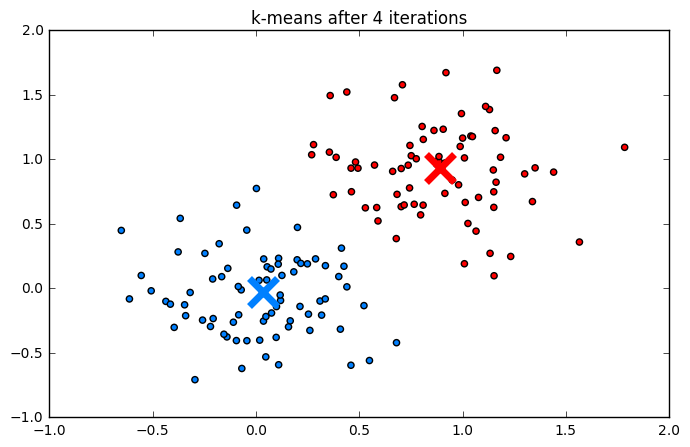
Кластеризация рукописных цифр (MNIST): Если кластеризовать уменьшенные до двух измерений с помощью метода главных компонент данные датасета Digits (рукописные цифры [1]), то разбиение на кластера будет следующим [2]:

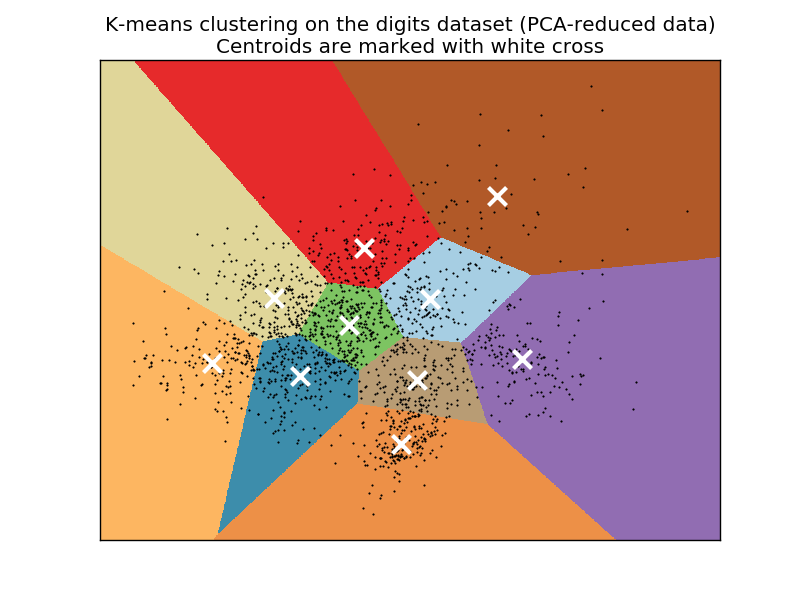
Метод всегда возвращает $K$ кластеров, где $K$ специфицированно пользователем, даже если кластерная структура в данных реально отсутствует, как на примере ниже:

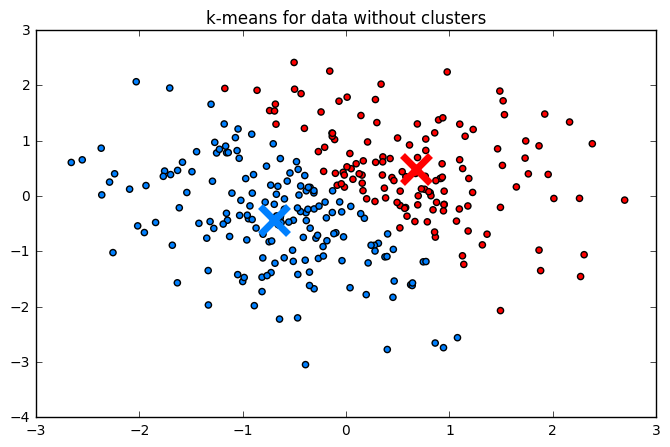
Ограничения метода

Выбор Евклидова расстояния накладывает строгие ограничения на форму получаемых кластеров. Действительно, объект $\boldsymbol{x}$ сильнее принадлежит $i$-му, а не $j$-му кластеру, если выполняется условие:

$$\|\boldsymbol{x} - \boldsymbol{\mu}_i\| < \|\boldsymbol{x} - \boldsymbol{\mu}_j\|$$

Это уравнение задает линейную полуплоскость. Множество объектов $i$-го кластера будет получаться пересечением всех таких полуплоскостей

$$\{\boldsymbol{x}: \|\boldsymbol{x} - \boldsymbol{\mu}_i\| < \|\boldsymbol{x} - \boldsymbol{\mu}_j\|,\; \forall j\ne i\}$$

и представлять собой выпуклый многогранник. Таким образом, алгоритм конструктивно не сможет выделять невыпуклые кластеры, как на примере ниже:

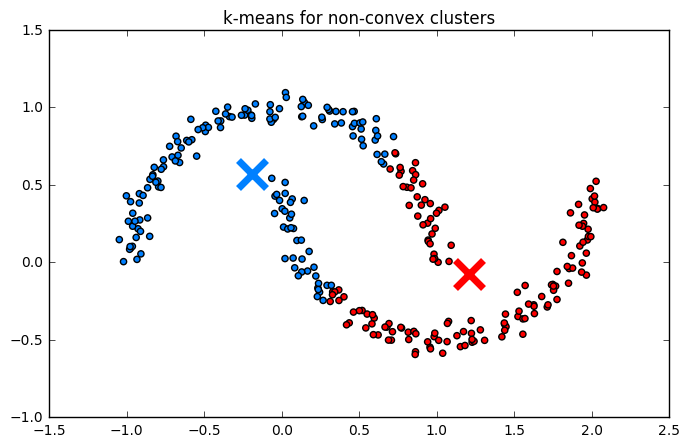
Также алгоритм стремится минимизировать дисперсию во всех направлениях одинаково. Это означает неявное предположение, что кластеры имеют сферическую форму, поэтому он будет плохо справляться с выделением сильно вытянутых кластеров.

Из равномерности учёта всех расстояний следует предположение, что кластера имеют примерно одинаковый размер.

Ограничения K-means

Алгоритм K-means плохо работает с невыпуклыми кластерами (например, "два полумесяца") и может находить кластеры там, где их нет (на равномерном распределении).

Алгоритмическая сложность

Вычислительная сложность алгоритма Ллойда оценивается как $O(I \cdot N \cdot K \cdot D)$, где:

• $N$ — количество объектов в выборке;
• $K$ — количество кластеров;
• $D$ — размерность пространства признаков;
• $I$ — количество итераций до сходимости.

Действительно, алгоритм состоит из итеративного повторения двух основных шагов. Рассмотрим сложность одной итерации:

1. Шаг назначения (Assignment Step): На этом этапе для каждого из $N$ объектов необходимо найти ближайший центроид.

   • Чтобы вычислить квадрат Евклидова расстояния $\|\boldsymbol{x}_n - \boldsymbol{\mu}_k\|^2$ между одним объектом и одним центроидом, требуется $O(D)$ операций.
   • Это вычисление проводится для каждого из $K$ центроидов.
   • Следовательно, для одного объекта сложность поиска ближайшего центра составляет $O(K \cdot D)$.
   • Для всех $N$ объектов суммарная сложность шага: $O(N \cdot K \cdot D)$.

2. Шаг обновления (Update Step): На этом этапе пересчитываются координаты центров.

   • Для вычисления нового центра $\boldsymbol{\mu}_k$ необходимо просуммировать векторы всех объектов, попавших в кластер $C_k$, и разделить на их количество.
   • Сложение двух векторов размерности $D$ требует $O(D)$ операций.
   • Поскольку каждый из $N$ объектов принадлежит ровно одному кластеру, он участвует в суммировании ровно один раз за итерацию.
   • Следовательно, суммарная сложность пересчета всех центров составляет $O(N \cdot D)$.

Линейная масштабируемость

Важной особенностью K-Means является то, что его сложность линейно зависит от количества объектов $N$. Это делает алгоритм пригодным для обработки больших массивов данных, в отличие от многих других методов кластеризации, имеющих более высокий порядок сложности по $N$.

Алгоритмические оптимизации

Стандартный алгоритм Ллойда на каждой итерации вычисляет расстояния от каждого объекта до всех $K$ центров. Существуют алгоритм Элкана [3], ускоряющий этот процесс (ценой увеличенных расходов на память), который основан на использовании неравенства треугольника для расстояний:

$$\|\boldsymbol{x} - \boldsymbol{\mu}_j\| \ge \|\boldsymbol{\mu}_i - \boldsymbol{\mu}_j\| - \|\boldsymbol{x} - \boldsymbol{\mu}_i\|$$

Это позволяет отбрасывать далекие центры без явного вычисления расстояний до них, если известно, что объект уже достаточно близок к своему текущему центру.

Ускорение достигается ценой повышенных расходов на память $O(N\cdot K)$ для промежуточных переменных.

Mini-batch K-means

Для больших очень данных используется стохастическая версия алгоритма - K-средних на минибатчах (Mini-batch K-means [4]), представляющий собой аналог алгоритма стохастического градиентного спуска.

Обозначим $N(k)$ — текущее число элементов кластера $k$. Тогда алгоритм работает следующим образом:

1. Инициализировать $\boldsymbol{\mu}_k$ (случайно).

2. Повторять до сходимости:

   • Сэмплировать минибатч случайных объектов $\mathbf{x}'_b, \quad b=1,2,...B$.

   • Для $b=1,2,...B$:

     • определить кластер $z_b$ для $\mathbf{x}'_b$ (по принципу ближайшего центроида).

     • Обновить размер кластера: $N(z_b) := N(z_b)+1$.

     • Обновить центроид кластера:

       $$\boldsymbol{\mu}_{z(b)}:=\left(1-\frac{1}{N(z_b)}\right)\boldsymbol{\mu}_{z(b)}+\frac{1}{N(z_b)}\mathbf{x}'_b$$

Выходом алгоритма являются центроиды $\boldsymbol{\mu}_1,...\boldsymbol{\mu}_K$ по близости к которым можно кластеризовать любые данные.

K-средних на минибатчах существенно ускоряет сходимость на очень больших данных ценой небольшого снижения качества [5]:

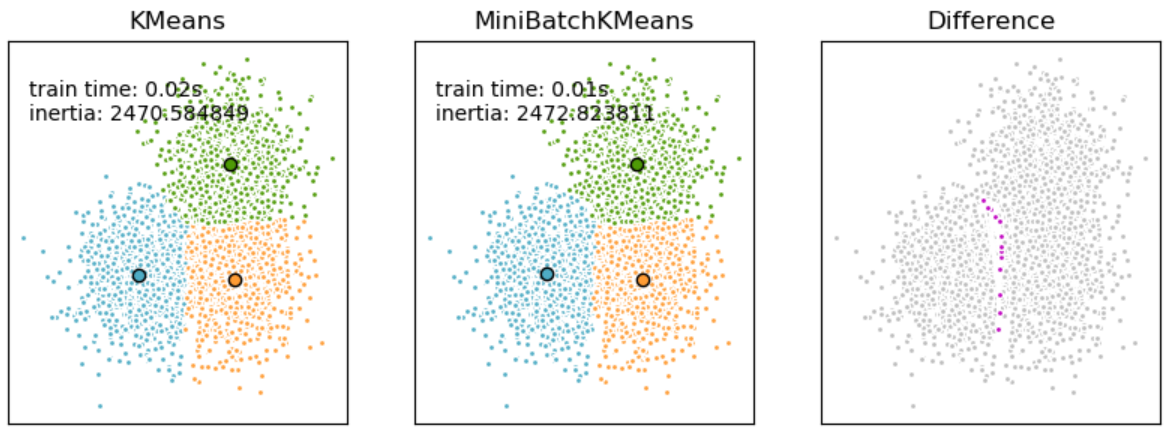
Ядерное обобщение K-средних

Метод K-средних выделяет лишь линейные границы между кластерами, а границы кластеров могут иметь только выпуклую форму. Однако метод K-средних допускает ядерное обобщение (Kernel K-means), которое способно сделать границы между классами нелинейными, а выделяемые области каждого класса - невыпуклыми, как показано на примере ниже:

Ядерное обобщение соответствует обычному методу K-средних, но не в исходном пространстве $\boldsymbol{x}$, а в новом пространстве $\phi(\boldsymbol{x})$, которое называемом спрямляющим.

При этом центроиды кластеров формально вычисляются по формуле

$$\boldsymbol{\mu}_i = \frac{1}{|C_i|}\sum_{n \in C_i} \phi(\boldsymbol{x}_n),$$

но напрямую не вычисляются, поскольку спрямляющее пространство может быть сложной структуры и даже бесконечномерным.

Расстояние от объекта до центроида кластера вычисляется по формуле:

$$\rho(\boldsymbol{x}, \boldsymbol{\mu}_i)^2 = \|\phi(\boldsymbol{x}) - \boldsymbol{\mu}_i\|^2$$

Воспользуемся тем, что квадрат L2-нормы можно вычислить через скалярное произведение, а также свойствами скалярного произведения:

$$\|\phi(\boldsymbol{x}) - \boldsymbol{\mu}_i\|^2 = \langle\phi(\boldsymbol{x}) - \boldsymbol{\mu}_i, \phi(\boldsymbol{x}) - \boldsymbol{\mu}_i \rangle = \langle \phi(\boldsymbol{x}), \phi(\boldsymbol{x}) \rangle - 2\langle \phi(\boldsymbol{x}), \boldsymbol{\mu}_i \rangle + \langle \boldsymbol{\mu}_i, \boldsymbol{\mu}_i \rangle$$

Теперь выразим каждое слагаемое через функцию ядра

$$K(\boldsymbol{x},\boldsymbol{x}') = \langle\phi(\boldsymbol{x}), \phi(\boldsymbol{x}') \rangle$$

1. Первое слагаемое:

   $$\langle \phi(\boldsymbol{x}), \phi(\boldsymbol{x}) \rangle = K(\boldsymbol{x}, \boldsymbol{x})$$

2. Второе слагаемое:

   $$2\langle \phi(\boldsymbol{x}), \frac{1}{|C_i|}\sum_{n \in C_i} \phi(\boldsymbol{x}_n) \rangle = \frac{2}{|C_i|} \sum_{n \in C_i} K(\boldsymbol{x}, \boldsymbol{x}_n)$$

3. Третье слагаемое:

   $$\langle \frac{1}{|C_i|}\sum_{n \in C_i} \phi(\boldsymbol{x}_n), \frac{1}{|C_i|}\sum_{m \in C_i} \phi(\boldsymbol{x}_m) \rangle = \frac{1}{|C_i|^2} \sum_{n \in C_i} \sum_{m \in C_i} K(\boldsymbol{x}_n, \boldsymbol{x}_m)$$

Итоговая формула:

$$\rho(\boldsymbol{x}, \boldsymbol{\mu}_i)^2 = \underbrace{K(\boldsymbol{x}, \boldsymbol{x})}_{\text{Const по } i} - \underbrace{\frac{2}{|C_i|} \sum_{n \in C_i} K(\boldsymbol{x}, \boldsymbol{x}_n)}_{\text{Средняя близость к объектам кластера}} + \underbrace{\frac{1}{|C_i|^2} \sum_{n \in C_i} \sum_{m \in C_i} K(\boldsymbol{x}_n, \boldsymbol{x}_m)}_{\text{Компактность кластера}}$$

Алгоритм Ядерного K-средних

В отличие от стандартного K-means, здесь мы не можем явно хранить и пересчитывать координаты центров $\boldsymbol{\mu}_i$. Вместо этого состояние алгоритма определяется текущим распределением объектов по кластерам (метками $z_n$), которые неявно задают центроиды в спрямляющем пространстве.

Вход:

• $\mathbf{X} = \{\boldsymbol{x}_1, \dots, \boldsymbol{x}_N\}$ — набор данных.
• $K$ — число кластеров.
• $K(\cdot, \cdot)$ — функция ядра (например, RBF: $e^{-\gamma\|\boldsymbol{x}-\boldsymbol{x}'\|^2}$).

Алгоритм:

1. Инициализация: Случайным образом назначить начальные метки кластеров $z_n \in \{1, \dots, K\}$ для всех объектов $n=1, \dots, N$. Это определяет начальные множества $C_1, \dots, C_K$.

2. Повторять до сходимости:

   1. Для каждого кластера $i=1, \dots, K$ вычислить слагаемое, отвечающее за его компактность (не зависит от текущего объекта $\boldsymbol{x}$):

      $$L_i = \frac{1}{|C_i|^2} \sum_{n \in C_i} \sum_{m \in C_i} K(\boldsymbol{x}_n, \boldsymbol{x}_m)$$

   2. Для каждого объекта $n=1, \dots, N$:

      • Вычислить расстояние от $\boldsymbol{x}_n$ до центра каждого кластера $i$:
      $$d^2(\boldsymbol{x}_n, i) = L_i - \frac{2}{|C_i|} \sum_{m \in C_i} K(\boldsymbol{x}_n, \boldsymbol{x}_m)$$

      (Примечание: слагаемое $K(\boldsymbol{x}_n, \boldsymbol{x}_n)$ опущено, так как оно одинаково для всех $i$ и не влияет на выбор минимума).

      • Назначить новый кластер:
      $$z_n = \arg\min_{i} d^2(\boldsymbol{x}_n, i)$$

3. Вернуть $z_1, \dots, z_N$.

Вычислительная сложность

Недостатком kernel K-means является высокая вычислительная сложность. Чтобы вычислить расстояние от одного объекта до центра кластера $i$, нужно просуммировать значения ядра со всеми объектами этого кластера. Суммарная сложность одной итерации составляет $O(N^2)$. Это делает метод неприменимым для больших выборок.

Литература

1. Репозиторий UCI: Optical Recognition of Handwritten Digits.
2. Документация sklearn: A demo of K-Means clustering on the handwritten digits data.
3. Elkan C. Using the triangle inequality to accelerate k-means //Proceedings of the 20th international conference on Machine Learning (ICML-03). – 2003. – С. 147-153.
4. Sculley D. Web-scale k-means clustering //Proceedings of the 19th international conference on World wide web. – 2010. – С. 1177-1178.
5. Документация sklearn: Mini Batch K-Means.