Настройка на разных фрагментах обучающей выборки

Идеи методов

Пусть исходная обучающая выборка состоит из $N$ объектов. Для генерации разнообразных моделей из одного семейства чаще всего используется настройка моделей на разных фрагментах обучающей выборки $(X,Y)$ .

Чтобы настроить $M$ моделей, необходимо по единообразной схеме сгенерировать M фрагментов выборки $(X_1,Y_1),(X_2,Y_2),...(X_M,Y_M)$ , называемых псевдовыборками. На каждой псевдовыборке настраивается модель одного класса (как правило, решающее дерево). Но настроенные модели будут получаться разными, поскольку они настраиваются на разных наборах объектов!

Агрегация базовых моделей

Поскольку все псевдовыборки строятся по единообразной схеме, а базовые модели берутся из одного семейства, полученные базовые алгоритмы будут однородны и равнозначны между собой. Поэтому в качестве агрегирующей функции используется равномерное усреднение:

\hat{y}(\mathbf{x})=\frac{1}{M}\sum_{m=1}^M f_m(\mathbf{x})

Процесс построения ансамбля по разным псевдовыборкам показан на схеме ниже:

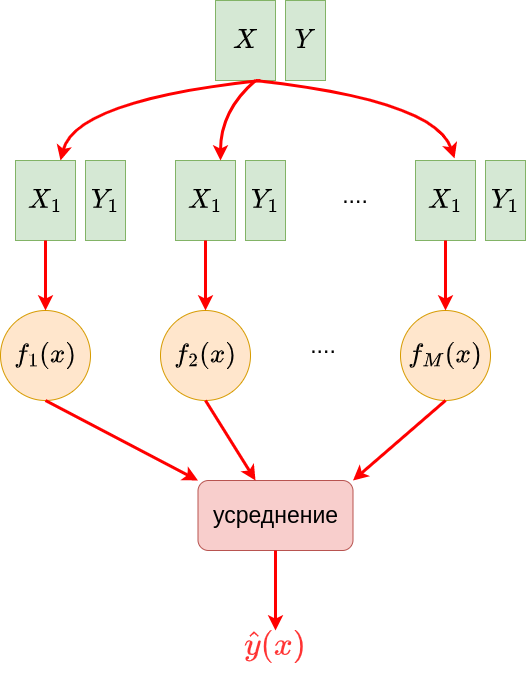
Для генерации псевдовыборок используются следующие подходы:

Кросс-валидация (cross-validation): вся выборка разбивается по объектам на $M$ случайных блоков одного размера. $m$ -я псевдовыборка включает все блоки, кроме блока $m$ , $m=1,2,...M$ . Это аналогично кросс-валидации при оценке качества прогнозов. В результате каждая модель будет настраиваться, используя примерно $N\frac{M-1}{M}$ объектов.
Бэггинг (bagging): псевдовыборка генерируется такого же размера, что и исходная выборка, с помощью сэмплирования объектов с возвращением (with replacement). В результате некоторые объекты могут появиться в псевдовыборке несколько раз, а некоторые - ни разу. Если быть точнее, то вероятность не выбрать определённый объект равна $\frac{N-1}{N}$ , а вероятность не выбрать его $N$ раз равна $\left(\frac{N-1}{N}\right)^N$ . При $N\to\infty$ она будет стремиться к $1/e \approx 0.37$ (докажите!), в результате чего псевдовыборка будет содержать примерно 2/3 исходных объектов, но её размер будет по-прежнему $N$ за счёт того, что некоторые объекты используются несколько раз. Псевдовыборка, полученная таким образом, называется бустраповской псевдовыборкой (bootstrap sample [1], предложена в [2]) и широко используется в статистике для получения эмпирических распределений тестовых статистик.
Пэйстинг (pasting): псевдовыборка генерируется из исходной с помощью сэмплирования объектов без возвращения (without replacement). Чтобы псевдовыборка получалась отличной от исходной, необходимо, чтобы размер псевдовыборки был строго меньше $N$ . Пэйстинг удобен для больших данных, где бэггинг слишком ресурсоёмок.
Метод случайных подпространств (random subspaces): в этом методе берутся все объекты исходной выборки, а сэмплируются признаки без возвращения. Модель, обученная на такой выборке, будет использовать лишь часть от всех располагаемых признаков.
Метод случайных фрагментов (random patches [3]): комбинируется сэмплирование объектов и признаков без возвращения. Это практично, когда приходится работать как с большим объёмом объектов, так и признаков. Вариация метода - сэмплировать объекты с возвращением, как в бэггинге.

Ниже показано сравнение регрессионных прогнозов для одного решающего дерева и для бэггинга над решающими деревьями:

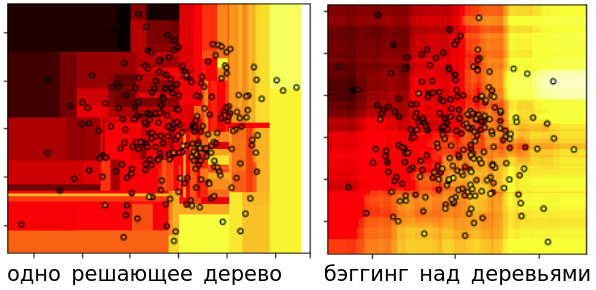
Видно, что одно решающее дерево даёт кусочно-постоянное решение с более резкими перепадами прогнозов по сравнению с ансамблем над многими деревьями.

Во всех представленных методах можно варьировать число псевдовыборок $M$ . Поскольку на каждой псевдовыборке настраивается модель одного типа, то все базовые алгоритмы равнозначны, поэтому их прогнозы в итоге усредняются с равными весами.

При увеличении числа базовых алгоритмов качество может только увеличиваться. Вначале оно резко падает (поскольку малое число псевдовыборок охватывает далеко не все данные), а потом выходит на стабильную асимптоту, как показано на рисунке ниже:

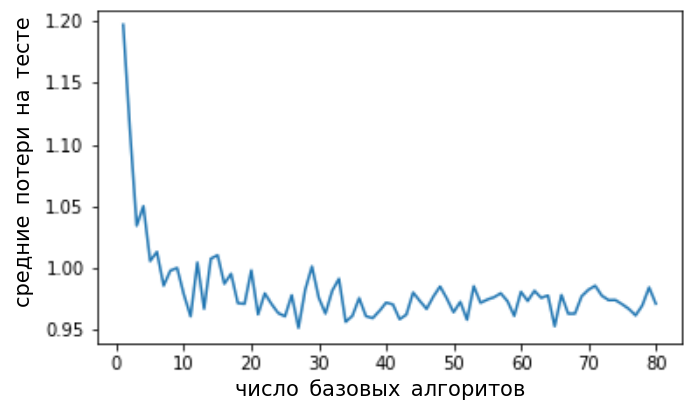
Поэтому по гиперпараметру $M$ нельзя переобучиться: качество может только вырасти или остаться прежним, если $M$ взять слишком большим.

Однако сложность настройки ансамбля и построения прогнозов линейно растёт с ростом числа базовых моделей. Поэтому на практике подбирают оптимальные значения других гиперпараметров (например, функцию неопределённости, минимальное число объектов в листах при настройке ансамбля над решающими деревьями) при невысоком $M$ , а в финальной версии модели увеличивают $M$ при уже настроенных гиперпараметрах.

Неопределённость прогноза

Поскольку все базовые модели равнозначны между собой, можно рассчитывать не только среднее от их прогнозов $f_1(\mathbf{x}),...f_M(\mathbf{x})$ , но и стандартное отклонение, которое будет показывать неопределённость прогноза. Это повышает прозрачность использования модели, поскольку даёт возможность дифференцировать ситуации, когда ансамбль уверен в своём прогнозе, а когда - нет. В последнем случае можно передать объект на обработку другому более продвинутому методу.

С представленными методами генерации ансамблей можно также ознакомиться в [4].

Оценка Out-of-Bag

Честная оценка качества модели требует выделения отдельной валидационной выборки или процедуры кросс-валидации, что сокращает объём данных для обучения модели. Метод оценивания out-of-bag (OOB estimate) позволяет использовать ту же обучающую выборку для оценивания качества ансамбля, что использовалась для его настройки, и применим к методам, в которых базовые модели обучаются на подмножествах объектов: кросс-валидация, бэггинг, пэйстинг и метод случайных фрагментов.

Поскольку каждая базовая модель использует не все, а лишь подмножество объектов обучающей выборки, то для каждого объекта $(\mathbf{x}_n,y_n)$ можно составить множество $I(n)$ тех псевдовыборок (и соответствующих базовых моделей), куда этот объект не попал. Далее мы можем получить честный прогноз для $\mathbf{x}_n$ , усредняя не по всем базовым моделям, а только по подмножеству моделей, обучающие псевдовыборки которых не содержали выбранный объект:

\hat{y}(\mathbf{x})=\frac{1}{|I(\mathbf{x}_n)|}\sum_{i\in I(n)}f_i(\mathbf{x}_n)

Для моделей, проиндексированных $I(n)$ , объект $\mathbf{x}_n$ будет новым, и в результате мы построим честный вневыборочный прогноз, не прибегая к отдельной валидационной выборке. Out-of-Bag-оценка (OOB-estimate [5]) строится указанным способом, усредняя out-of-bag прогнозы по всем объектам обучающей выборки.

Как в среднем связана OOB-оценка со средними потерями на тестовой выборке?

OOB-оценка несмещённо оценивает качество ансамбля, использующего не все, а лишь подмножество базовых моделей. Итоговая же модель использует все базовые модели. Чем количество базовых моделей больше, тем прогноз получается точнее в общем случае, поэтому реальное качество на тестовой выборке будет в среднем даже немного выше, чем оценка out-of-bag.

Пример запуска на Python

Бэггинг для классификации:

from sklearn.ensemble import BaggingClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import accuracy_score
from sklearn.metrics import brier_score_loss

X_train, X_test, Y_train, Y_test = get_demo_classification_data()  

# инициализация модели:
model = BaggingClassifier(DecisionTreeClassifier(),  # базовая модель
                          max_samples=0.8,           # доля случайных объектов для обучения
                          max_features=1.0,          # доля случайных признаков для обучения
                          n_jobs=-1)                 # использовать все ядра процессора
model.fit(X_train, Y_train)    # обучение модели   
Y_hat = model.predict(X_test)  # построение прогнозов
print(f'Точность прогнозов: {100*accuracy_score(Y_test, Y_hat):.1f}%')

P_hat = model.predict_proba(X_test)  # можно предсказывать вероятности классов
loss = brier_score_loss(Y_test, P_hat[:,1])  # мера Бриера на вероятности положительного класса
print(f'Мера Бриера ошибки прогноза вероятностей: {loss:.2f}')

Бэггинг для регрессии:

from sklearn.ensemble import BaggingRegressor
from sklearn.tree import DecisionTreeRegressor
from sklearn.metrics import mean_absolute_error

X_train, X_test, Y_train, Y_test = get_demo_classification_data()  

# инициализация модели:
model = BaggingRegressor(DecisionTreeRegressor(),  # базовая модель
                         max_samples=0.8,          # доля случайных объектов для обучения
                         max_features=1.0,         # доля случайных признаков для обучения
                         n_jobs=-1)                # использовать все ядра процессора
model.fit(X_train, Y_train)    # обучение модели   
Y_hat = model.predict(X_test)  # построение прогнозов
print(f'Средний модуль ошибки (MAE): {mean_absolute_error(Y_test, Y_hat):.2f}')    

Больше информации. Полный код.

Настройка на разных фрагментах обучающей выборки

Идеи методов​

Оценка Out-of-Bag​

Пример запуска на Python​

Литература​

Идеи методов

Оценка Out-of-Bag

Пример запуска на Python

Литература