Перейти к основному содержимому

Стохастический градиентный спуск с инерцией

Метод стохастического градиентного спуска с инерцией (stochastic gradient descent with momentum, SGD+momentum) позволяет ускорить сходимость и предотвратить застревание метода стохастического градиентного спуска в локальных минимумах с небольшой окрестностью. Также он позволяет быстрее проскакивать точки перегиба и другие области медленных изменений функции потерь

Перепишем метод обычного стохастического градиентного спуска в эквивалентном виде:

инициализируем t=0t=0, а начальные веса w0\mathbf{w}_0 случайно

пока не выполнено условие остановки:

            сэмплируем случайные объекты I={n1,...nK}I=\{n_1,...n_K\} из {1,2,...N}\{1,2,...N\}

            Δwt+1:=εt1K∑n∈I∇wL(xn,yn∣wt)\Delta \mathbf{w}_{t+1} := \varepsilon_t \frac{1}{K} \sum_{n\in I} \nabla_\mathbf{w} \mathcal{L}(\mathbf{x}_n,y_n|\mathbf{w}_t)

            wt+1:=wt−Δwt+1\mathbf{w}_{t+1}:= \mathbf{w}_t- \Delta \mathbf{w}_{t+1}

            t:=t+1t:=t+1

Метод стохастического градиентного спуска с инерцией считается аналогично, но в качестве вектора сдвига весов используется не только градиент по объектам минибатча, но и ранее посчитанные градиенты с небольшим весом, задаваемым гиперпараметром μ∈(0,1)\mu\in (0,1):

инициализируем t=0t=0, а начальные веса w0\mathbf{w}_0 случайно

пока не выполнено условие остановки:

            сэмплируем случайные объекты I={n1,...nK}I=\{n_1,...n_K\} из {1,2,...N}\{1,2,...N\}

            Δwt+1:=μΔwt+εt1K∑n∈I∇wL(xn,yn∣wt)\Delta \mathbf{w}_{t+1} := \textcolor{red}{\mu\Delta \mathbf{w}_t}+\varepsilon_t \frac{1}{K} \sum_{n\in I} \nabla_\mathbf{w} \mathcal{L}(\mathbf{x}_n,y_n|\mathbf{w}_t)

            wt+1:=wt−Δwt+1\mathbf{w}_{t+1}:= \mathbf{w}_t- \Delta \mathbf{w}_{t+1}

            t:=t+1t:=t+1

Компонента μΔwt\mu\Delta \mathbf{w}_t называется инерцией (momentum) и позволяет ускорить сходимость за счёт объединения информации о текущем градиенте с ранее посчитанными градиентами. За счёт этого градиент получается менее зашумлённым случайностью выбора объектов текущего минибатча, что позволяет использовать более высокий шаг обучения и ускорить сходимость. Отметим однако, что выбор высокого μ\mu делает метод менее чувствительным к текущему направлению максимального снижения функции, что может наоборот замедлить сходимость. На практике чаще всего используют μ=0.9\mu=0.9.

Рекурсивно подставляя вместо Δwt,Δwt−1,Δwt−2,...\Delta \mathbf{w}_{t},\Delta \mathbf{w}_{t-1},\Delta \mathbf{w}_{t-2},... формулу их расчёта, получим, что изменение весов Δwt+1\Delta \mathbf{w}_{t+1} зависит от всех ранее посчитанных градиентов с экспоненциально убывающими весами по номеру итерации.

Другим достоинством внесения инерции в обновление весов является то, что она позволяет проскакивать локальные минимумы с малой окрестностью, сходясь к более устойчивым минимумам с большей окрестностью, как показано на рисунке:

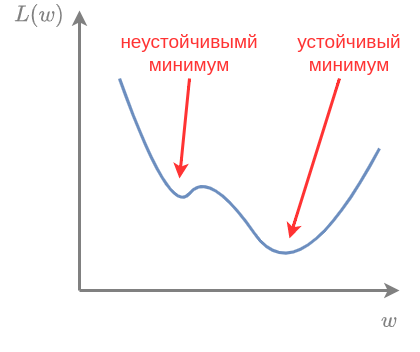
robust-minimum.png

Инерция Нестерова​

Метод инерции Нестерова (Nestrov momentum) позволяет ещё немного ускорить сходимость за счёт того, что градиент будет считаться в точке, более близкой к новой оценке весов на следующей итерации:

инициализируем t=0t=0, а начальные веса w0\mathbf{w}_0 случайно

пока не выполнено условие остановки:

            сэмплируем случайные объекты I={n1,...nK}I=\{n_1,...n_K\} из {1,2,...N}\{1,2,...N\}

            Δwt+1:=μΔwt+εt1K∑n∈I∇wL(xn,yn∣wt−μΔwt)\Delta \mathbf{w}_{t+1} := \mu\Delta \mathbf{w}_t+\varepsilon_t\frac{1}{K} \sum_{n\in I} \nabla_\mathbf{w} \mathcal{L}(\mathbf{x}_n,y_n|\mathbf{w}_t\textcolor{red}{-\mu\Delta \mathbf{w}_t})

            wt+1:=wt−Δwt+1\mathbf{w}_{t+1}:= \mathbf{w}_t-\Delta \mathbf{w}_{t+1}

            t:=t+1t:=t+1

На шаге tt мы уже заранее знаем, что веса сдвинутся на величину инерции, поэтому можем считать градиент уже в сдвинутой точке. Подобное заглядывание вперёд позволяет заранее сместить градиент, если на следующей итерации предвидится изменение рельефа функции потерь.

Более продвинутые техники

Для оптимизируемых функций со сложным рельефом (особенно в настройке нейросетей) применяются более продвинутые методы, такие как RMSprop и Adam, ключевая идея которых заключается в том, что шаг обучения εt\varepsilon_t вычисляется независимо для каждой компоненты вектора весов. Это связано с тем, что вдоль одних осей в пространстве весов функция потерь меняется быстро, а вдоль других - медленно, поэтому, для ускорения сходимости, целесообразно адаптировать шаг обучения индивидуально для каждой оси.