Перейти к основному содержимому

Метод градиентного спуска

Идея метода​

Метод градиентного спуска (gradient descent [1]) минимизирует функцию потерь, итеративно сдвигая веса на антиградиент этой функции с небольшим весом.

Псевдокод метода:

инициализируем w\mathbf{w} случайно

пока не выполнено условие остановки:

             w:=w−ε∇wL(w)\mathbf{w}:=\mathbf{w}-\varepsilon\nabla_{\mathbf{w}}L(\mathbf{w})

Здесь ε>0\varepsilon>0 - гиперпараметр, характеризующий шаг обновления весов (learning rate). Он выбирается небольшой константой.

В качестве условия остановки обычно выбирается условие, что от итерации к итерации функция потерь перестаёт существенно меняться. Также можно допустить досрочное окончание оптимизации, если достигнуто максимальное число итераций.

Аналогия с путником в горах

Поскольку антиградиент −∇wL(w)-\nabla_{\mathbf{w}}L(\mathbf{w}) показывает локальное направление максимального уменьшения функции, метод градиентного спуска можно уподобить путнику, заблудившемуся ночью в горах, который, пытаясь спуститься вниз как можно быстрее, каждый раз делает шаг в направлении наиболее крутого склона.

Кстати, так можно и скатиться с обрыва! Чтобы не улететь, путник использует альпинистское снаряжение, чтобы упасть не больше чем на длину страхующей веревки. Аналогично и в методе градиентного спуска, если рельеф функции потерь резко меняется, то можно допускать сдвиги по величие не больше, чем на заранее заданный порог безопасности, ограничивая норму градиента, на который осуществляют сдвиг:

w:={w−ε∇wL(w), если ∥∇wL(w)∥<hw−ε∇whL(w)/∥L(w)∥, иначе. \mathbf{w}:= \begin{cases} \mathbf{w}-\varepsilon\nabla_{\mathbf{w}}L(\mathbf{w}), \text{ если }\|\nabla_{\mathbf{w}}L(\mathbf{w})\|<h \\ \mathbf{w}-\varepsilon\nabla_{\mathbf{w}}h L(\mathbf{w})/\|L(\mathbf{w})\|, \text{ иначе. } \end{cases}

Такой подход называется обрезкой градиента (gradient clipping [1]) и часто используется в настройке нейросетей, где функция потерь имеет сложный рельеф с резкими перепадами. Эта проблема особенно актуальна при настройке сложных нейросетевых моделей.

Выбор шага обучения​

Гиперпараметр ε>0\varepsilon>0 выбирается пользователем и представляет собой небольшую величину, влияющую на характер сходимости. Если ε\varepsilon выбрать слишком малым, то потребуется очень много шагов оптимизации, чтобы дойти до минимума. Если, наоборот, его выбрать слишком большим, то метод может расходиться. Эти ситуации показаны на рисунке слева и справа соответственно:

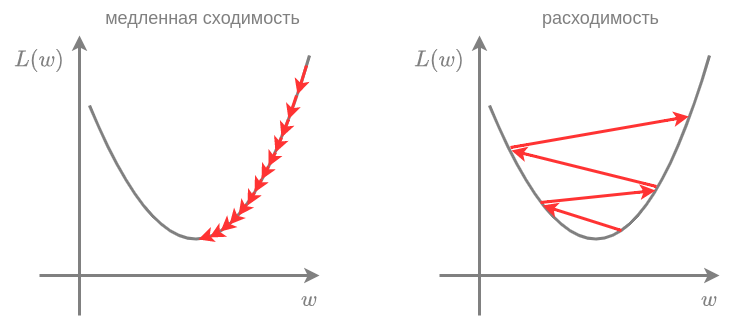
convergence.png

Для подбора ε\varepsilon необходимо построить зависимость функции потерь L(wt)L(\mathbf{w}_t) от номера итерации tt и выбрать ε\varepsilon таким, чтобы сходимость была максимально быстрой, и не возникало расходимости:

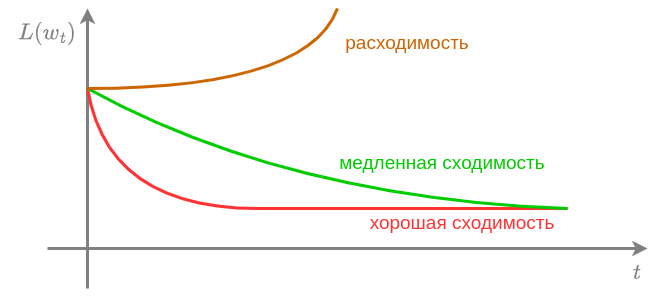
convergence-control.png

Ускорение сходимости

Дополнительно ускорить сходимость может нормализация признаков (приведение их к одному масштабу). Это позволяет отчасти решить проблему "вытянутых долин" в рельефе функции потерь, из-за которых приходится выбирать маленький шаг, чтобы не разойтись вдоль быстро меняющихся направлений.

Выбор начального приближения​

В методе градиентного спуска начальное значение весов w\mathbf{w} инициализируется случайно. В случае выпуклой функции потерь любой глобальный минимум является глобальным (докажите!), поэтому старт из разных начальных приближений приведёт к решению того же качества.

Если же функция потерь невыпукла, то она может содержать много локальных минимумов, и выбор начального приближения может влиять на то, к какому минимуму алгоритм оптимизации в итоге сойдётся! Поэтому для невыпуклых потерь предлагается запускать алгоритм несколько раз из разных начальных приближений, а потом выбрать наилучшее решение (обеспечивающее минимальное значение функции потерь).

Также стоит отметить, что выбор начального приближения ближе к предполагаемому минимуму уменьшит число итераций до сходимости и ускорит настройку модели.

Условия сходимости​

Для сходимости метода достаточно, чтобы функция потерь была непрерывно-дифференцируема, выпукла вниз в окрестности оптимума, удовлетворяла условию Липшица (имела ограниченную производную), а шаг обучения был достаточно мал. Детальнее об методе градиентного спуска, условиях и скорости его сходимости можно прочитать в [3].

Литература​

  1. Wikipedia: gradient descent.

  2. Geeksforgeeks: understanding gradient clipping.

  3. Ахмеров Р.Р. Методы оптимизации гладких функций.