Перейти к основному содержимому

Метод Ньютона

Метод оптимизации Ньютона (Newton's optimization method) позволяет ускорить метод градиентного спуска за счёт использования информации не только о градиенте, но и о матрице вторых производных, называемой матрицей Гессе (Hessian):

∇2L(w)=(∂L(w)∂w1∂w1⋯∂L(w)∂w1∂wD⋯⋯⋯∂L(w)∂wD∂w1⋯∂L(w)∂wD∂wD)∈RD×D\nabla^2 L(\mathbf{w})=\begin{pmatrix} \frac{\partial L(\mathbf{w})}{\partial w_1 \partial w_1} & \cdots & \frac{\partial L(\mathbf{w})}{\partial w_1 \partial w_D} \\ \cdots & \cdots & \cdots \\ \frac{\partial L(\mathbf{w})}{\partial w_D \partial w_1} & \cdots & \frac{\partial L(\mathbf{w})}{\partial w_D \partial w_D} \end{pmatrix} \in \mathbb{R}^{D \times D}

Использование вторых производный позволяет ускорить сходимость, поскольку содержит информацию о скорости изменения градиента. Там, где градиент меняется медленно, можно увеличить шаг обучения, а там, где быстро, - замедлить.

Метод Ньютона выглядит следующим образом:

инициализируем настраиваемые веса w\mathbf{w} случайно

пока не выполнено условие остановки:

             w:=w−[∇w2L(w)]−1∇wL(w)\mathbf{w}:=\mathbf{w}-[\nabla_{\mathbf{w}}^2 L(\mathbf{w})]^{-1}\nabla_{\mathbf{w}}L(\mathbf{w})

Как видим, за счёт использования информации о вторых производных удалось избавиться от явной спецификации шага обучения - он настраивается автоматически по скорости изменения градиента домножением на матрицу Гессе, состоящую из всех вторых производных функции потерь.

Обратим внимание, что домножение на матрицу подстраивает скорость изменения вдоль каждой оси, используя градиенты вдоль всех осей.

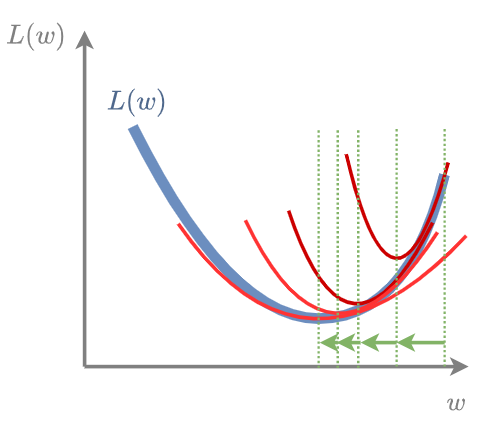
Геометрически метод Ньютона в каждой точке строит параболу (в многомерном пространстве - параболоид), после чего смещает оценку весов в точку минимума этой параболы:

Newton-convergence.png

Обоснование метода Ньютона​

Рассмотрим минимизацию дважды дифференцируемой функции потерь L(w)→min⁡wL(\mathbf{w})\to\min_{\mathbf{w}}

Пусть w∗=arg⁡min⁡wL(w)\mathbf{w}^{*}=\arg\min_{\mathbf{w}}L(\mathbf{w})

Тогда ∇L(w∗)=0\nabla L(\mathbf{w}^{*})=\mathbf{0}

Разложение Тейлора ∇L(w)\nabla L(\mathbf{w}) относительно w\mathbf{w} в точке w∗\mathbf{w}^{*}:

∇L(w∗)=0=∇L(w)+∇2L(w)(w∗−w)+o(∥w−w∗∥),\nabla L(\mathbf{w}^{*})=0=\nabla L(\mathbf{w})+\nabla^{2}L(\mathbf{w})(\mathbf{w}^{*}-\mathbf{w})+o(\left\lVert \mathbf{w}-\mathbf{w}^{*}\right\rVert ),

откуда

w∗−w=−[∇2L(w)]−1∇L(w)+o(∥w−w∗∥)\mathbf{w}^{*}-\mathbf{w}=-\left[\nabla^{2}L(\mathbf{w})\right]^{-1}\nabla L(\mathbf{w})+o(\left\lVert \mathbf{w}-\mathbf{w}^{*}\right\rVert )

Получаем итоговое правило обновления весов, чтобы (приближённо!) переместиться в точку минимума:

w:=w−[∇2L(w)]−1∇L(w)\mathbf{w} := \mathbf{w}-\left[\nabla^{2}L(\mathbf{w})\right]^{-1}\nabla L(\mathbf{w})

При минимизации квадратичной функции погрешности o(∥w−w∗∥)o(\left\lVert \mathbf{w}-\mathbf{w}^{*}\right\rVert ), её квадратичная аппроксимация будет точной, поэтому метод Ньютона сойдётся за один шаг.

Достоинства и недостатки метода​

Метод Ньютона обладает более высокой скоростью сходимости, чем метод градиентного спуска. В частности, он находит минимум квадратичного функционала всего лишь за одну итерацию. Однако практическому применению этого метода в машинному обучении мешают два аспекта:

  • Необходимость хранить в памяти матрицу Гессе, размера D×DD\times D, а DD обычно велико при большом числе признаков и при использовании таких перепараметризованных моделей, как нейросети.

  • Необходимость обращать матрицу Гессе на каждой итерации, что имеет вычислительную сложность O(D3)O(D^3).

Детальнее о проблемах применения метода Ньютона в машинном обучении можно прочитать обсуждении [1]. Из-за перечисленных проблем на практике чаще используют квазиньютоновские методы [2], которые используют вычислительно эффективную аппроксимацию метода Ньютона.

Детальнее о методе Ньютона, условиях сходимости и альтернативных методах второго порядка рекомендуется прочитать в учебнике ШАД [3].

Литература​

  1. Stats.stackexchange: Why is Newton's method not widely used in machine learning?

  2. Wikipedia: Quasi-Newton method.

  3. Учебник ШАД: методы второго порядка.