Перейти к основному содержимому

Мониторинг сходимости

Для анализа сходимости метода стохастического градиентного спуска важно смотреть на динамику потерь на каждой итерации алгоритма. Особенно это важно при долгой и трудоёмкой настройке нейросетей, чтобы на ранней стадии оптимизации увидеть некорректную настройку определённых параметров. Поскольку в стохастическом градиентном спуске сдвиг весов производится на антиградиент по случайному минибатчу объектов, то и величина этого сдвига будет подвержена случайным колебаниям, как в примере ниже:

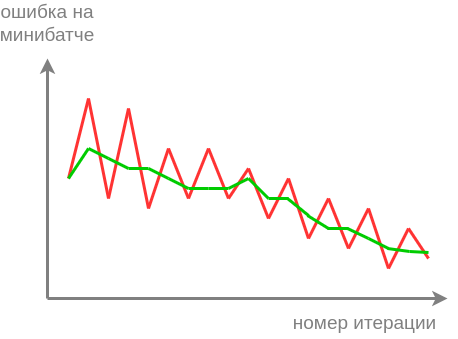
smoothed-loss.png

Для большей наглядности нам хотелось бы отслеживать сглаженную версию этой динамики, показанную зелёной кривой. Для этого существуют два подхода - скользящее среднее и экспоненциальное сглаживание. Оба метода на вход принимают зашумлённый временной ряд ztz_t (в нашем случае - потерь на объектах минибатча), а на выходе выдают его сглаженную версию sts_t, причем сглаживание осуществляется динамически в каждый момент времени.

Скользящее среднее​

Идея скользящего среднего заключается в выдаче усреднения по KK последним наблюдениям:

st=1K∑i=t−K+1tzis_t=\frac{1}{K}\sum_{i=t-K+1}^t z_i

Это среднее можно эффективно пересчитывать по формуле

st:=st−1+ztK−zt−KKs_t:=s_{t-1}+\frac{z_t}{K}-\frac{z_{t-K}}{K}

Вначале, пока KK наблюдений еще не накоплены, нужно усреднять по всем располагаемым наблюдениям.

Экспоненциальное сглаживание​

Экспоненциальное сглаживание вычисляет сглаженную версию временного ряда по следующей формуле:

{s1=z1st=(1−α)zt+αst−1\begin{cases} s_{1}=z_{1} & \\ s_{t}=(1-\alpha)z_{t}+\alpha s_{t-1} & \end{cases}

Гиперпараметр α∈[0,1)\alpha\in [0,1) управляет степенью сглаживания.

Как именно α\alpha влияет на результат?

Увеличение α\alpha приводит к более слабому учёту новых данных и к более сильному - исторических. Поэтому сглаженный временной ряд sts_t будет получаться более гладким. Уменьшение α\alpha уменьшает сглаживание. В частности, при α=0\alpha=0, сглаженный ряд совпадает с исходным.

Если рекуррентно переписать зависимость sts_t только от zt,zt−1,zt−2,...z_t,z_{t-1},z_{t-2},..., то получим, что экспоненциальное сглаживание выдаёт взвешенное усреднение по всем прошлым наблюдениям с экспоненциально убывающими весами:

st=(1−α)(zt+αzt−1+α2zt−2+α3zt−3+...)s_t = (1-\alpha)(z_{t}+\alpha z_{t-1}+\alpha^{2}z_{t-2}+\alpha^{3}z_{t-3}+...)

Более детально об экспоненциальном сглаживании и его связи со скользящим средним можно прочитать в [1].

Литература​

  1. Wikipedia: exponential smoothing.