Интерпретация решающего дерева

Решающее дерево является интерпретируемым алгоритмом машинного обучения. Интерпретация возможна:

• визуализацией решающего дерева;

• оценкой степени влияния каждого признака на прогнозы в среднем по выборке;

• оценкой степени влияния каждого признака на прогноз интересующего объекта.

Ниже мы рассмотрим каждый из подходов детально.

Визуализация деревьев

Решающее дерево небольшой глубины можно визуализировать и анализировать напрямую. В этом смысле это метод, обладающий глобальной интерпретируемостью.

Ниже приведён простой пример решающего дерева для задачи кредитного скоринга в банке, работу которого может понять даже не-специалист:

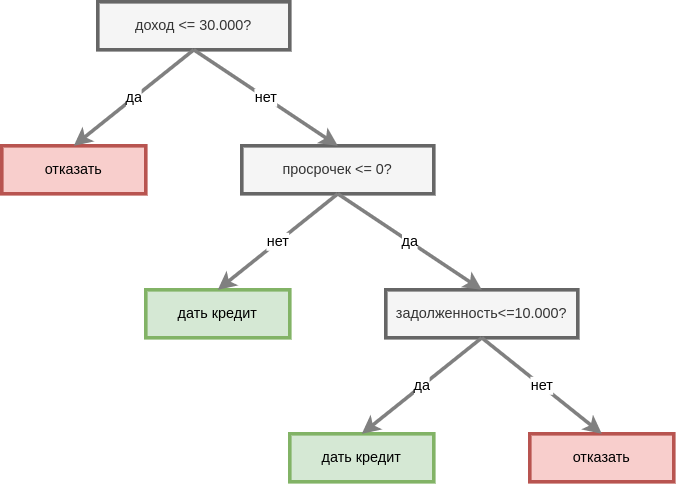
Глобальная важность признаков

Можно оценивать значимость каждого признака для прогнозов решающего дерева в целом по выборке, используя ранее уже изученное среднее изменение неопределённости (mean decrease in impurity, MDI).

Рассмотрим задачу wine [1], в которой по характеристикам вина требуется предсказать его класс. Значимости каждого признака приведены ниже [2]:

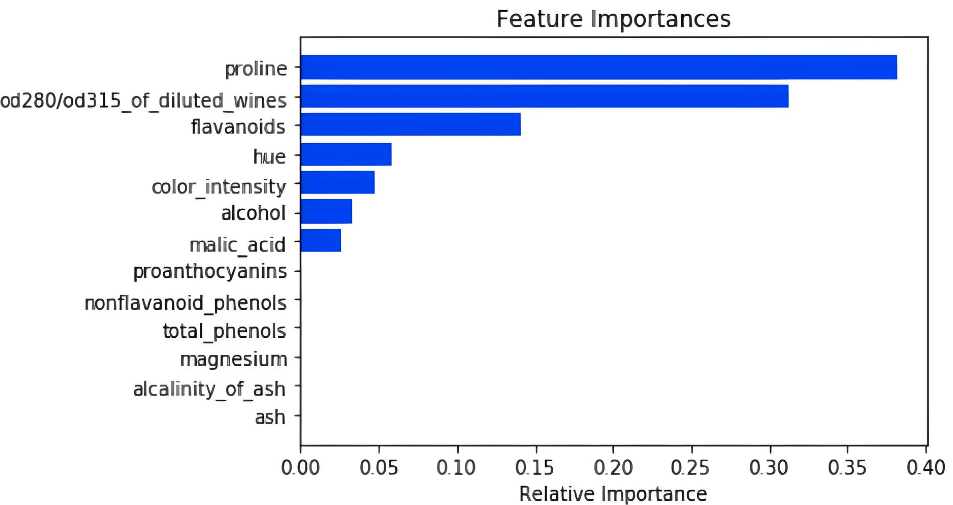
Из графика сразу видно, что уровень пролина оказывается самым важным признаком.

Эту же методику можно применять для ансамбля над решающими деревьями (бэггинг, случайный лес, бустинг и др.) - нужно лишь усреднить важности признаков каждого дерева с теми коэффициентами, с которыми оно учитываются в ансамбле.

Поскольку ансамбли дают более точные прогнозы, расчёт важности по ансамблю деревьев даст более надёжную оценку влияния признаков на отклик!

Первичный анализ данных

Анализ самых значимых признаков по ансамблю решающих деревьев - важный этап первичного анализа данных, который стоит применять, даже если вы не собираетесь впоследствии использовать сами решающие деревья!

Вклад признака в отдельный прогноз

Нас может интересовать вклад каждого признака не для всех объектов выборки, а для одного интересующего объекта $\mathbf{x}$. Рассмотрим, как это можно рассчитать.

Как известно в решающих деревьях прогноз приписывается каждому листу дерева простым усреднением откликов объектов, попавших в лист. В случае классификации усредняются one-hot закодированные метки классов, что на выходе даёт вектор предсказанных вероятностей классов. Но аналогично можно сопоставить прогноз и каждому промежуточному узлу, усредняя отклики объектов, прошедших через соответствующий узел.

Введём обозначения:

• $t$ - узел дерева,

• $\text{Parent}\left(t\right)$ - соответствующий родительский узел,

• $\text{root}$ - корень дерева,

• $\text{path}\left(\mathbf{x}\right)$ - путь от корня до листа, по которому объект $\mathbf{x}$ спустился вниз по дереву.

Посчитаем для объекта $\mathbf{x}$ прогноз $\widehat{y}\left(t\right)$ в каждом промежуточном узле дерева $t$ вдоль пути $\text{path}\left(\mathbf{x}\right)$. Итоговый прогноз можно декомпозировать по вкладу в него каждого узла:

$$\widehat{y}(\mathbf{x})=\sum_{t\in\text{path}\left(\mathbf{x}\right)\backslash\left\{ \text{root}\right\} }|\widehat{y}\left(t\right)-\widehat{y}\left(\text{Parent}\left(t\right)\right)|$$

Но нам нужен не вклад каждого узла, а вклад каждого признака в прогноз для интересующего объекта. Для этого для каждого признака $i$ найдём множество тех узлов $T_i$, где этот признак использовался в решающем правиле дерева.

Тогда вклад $i$-го признака в прогноз $\hat{y}(\mathbf{x})$ считается как суммарный вклад по узлам, учитывающим $i$-й признак:

$$\text{Importance}(i|\mathbf{x})=\sum_{t\in\text{path}\left(\mathbf{x}\right)\backslash\left\{ \text{root}\right\} \textcolor{red}{\cap T_i} }|\widehat{y}\left(t\right)-\widehat{y}\left(\text{Parent}\left(t\right)\right)|$$

Так мы рассчитаем вклад каждого признака в прогноз определённого объекта $\mathbf{x}$. Метод был предложен в [3].

Обратим внимание, что

$$\sum_i \text{Importance}(i|\mathbf{x}) = \hat{y}(\mathbf{x}),$$

причём часть признаков будут оказывать положительное, а часть - отрицательное влияние на величину прогноза.

Метод обобщается на ансамбль решающих деревьев (бэггинг, бустинг, решающий лес и др.): для этого нужно усреднить вклады признаков по деревьям ансамбля.

Глобальная важность признака

Усредняя оценку важности по всем объектам выборки, получим глобальную важность признака, похожую по смыслу на меру среднего изменения неопределённости. Первая мера оценивает среднее изменение прогноза при учёте признака, а вторая - среднее влияние признака на снижение неопределённости прогнозов.

---

Вы также можете прочитать про интерпретацию решающих деревьев в [4]. А в следующем разделе учебника мы изучим подходы интерпретации прогнозов сложных моделей (balck-box models), таких как ансамбли алгоритмов и нейронные сети.

Литература

1. UC Irvine Machine Learning Repository: wine dataset.

2. Kanoki.org: decision tree in sklearn.

3. Blog.datadive.net: interpreting random forests.

4. Molnar C. Interpretable machine learning. – Lulu. com, 2020: Decision Tree.