Интерпретация линейной регрессии

Предположения метода

Линейная регрессия строит прогноз по формуле:

$$\widehat{y}(\mathbf{x}) = w_{0}+w_{1}x^{1}+w_{2}x^{2}+...+w_{D}x^{D}$$

Модель использует достаточно сильные предположения о данных:

• каждый признак $x^{i}$ влияет на отклик линейно со своим фиксированным весом $\mathbf{w}_{i}$;

• характер этого влияния не зависит от значений остальных признаков.

На практике эти предположения, скорее всего, не выполнены, зато настроенная модель проста и легко поддаётся интерпретации.

Интерпретация весов

Веса линейной регрессии можно интерпретировать следующим образом:

• Знак веса $w_i$ определяет направленность влияния $i$-го признака на отклик. Признак с положительным весом положительно влияет на отклик, а с отрицательным - отрицательно.

• Величина веса $w_i$ определяет силу влияния: увеличение $x^i$ на единицу приводит к увеличению $y$ на $w_i$. В случае, если $x^i$ - бинарный признак (присутствие определённой характеристики), то $w_i$ показывает, насколько увеличился бы прогноз, если бы признак был активен.

  Например, если прогнозируем, за какое время спортсмен пробежит марафон, а $x^i=\mathbb{I}[\text{была травма}]$, то $w_i$ покажет, насколько изменится время забега при наличии травмы у спортсмена. Если $x^i$ является категориальным признаком (например, у какого тренера занимался спортсмен) и кодируется one-hot кодированием, то полезно одну из категорий назначить референсной и закодировать вектором из нулей [0,0,...,0] (например, категорию, что спортсмен учился без тренера). Тогда вес при каждом бинарном признаке one-hot кодирования показывает вклад методики обучения соответствующего тренера в результат забега.

• Модуль веса при признаке $|w_i|$ оценивает степень влияния признака на прогноз. Однако перед применением этой методики все признаки необходимо привести к единой шкале (нормализовать).

  Иначе уменьшение признака в K раз и перенастройка модели приведут к увеличению веса при нём в K раз, но это не будет означать, что признак стал в K раз более важным!

• В статистике существует асимптотическая оценка стандартного отклонения $\sigma_i$ для оценки веса $w_i$. Это позволяет визуализировать для каждого признака не только $w_i$, но и его стандартное отклонение.

  Если интервал $(-3\sigma_i+w_i, w_i+3\sigma_i)$ покрывает ноль, то можно говорить о статистически незначимом влиянии $i$-го признака на отклик.

  Для проверки значимости влияния признака этого же можно использовать и t-тест Стьюдента [1], основанный на t-статистике, равной $w_i/\sigma_i$. Можно на графике откладывать $w_i$ и соответствующий 95% интервал для этого теста, как показано на рисунке ниже [2] для задачи BikeSharing [3]:

  

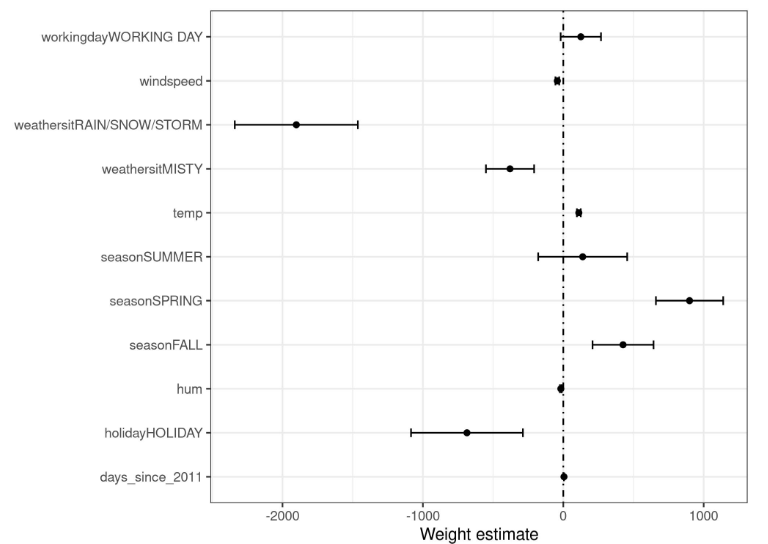
  Если интервал на графике покрывает ноль, то влияние признака на целевое значение статистически незначимо, иначе влияние считается значимым.

  Значимость влияния признака на отклик важна в таких задачах, как определение оптимального лечения заболевания. Если признак представляет собой объём выпитого лекарства, а выяснится, что влияние статистически незначимое, то нужно подбирать другие методы лечения!

Анализ аддитивных эффектов

Величина $w_{i}x^{i}$ характеризует аддитивный эффект, который i-й признак оказывает на прогноз для вещественного и бинарного признака. Перед использованием необходимо центрировать каждый признак, вычтя из него его среднее по всей выборке.

Визуализировать распределение аддитивных эффектов удобно, используя ящики с усами (boxplots [4]).

Построение ящика с усами

• Краями прямоугольника ("ящика") выступают 25% и 75% персентили $Q_1$ и $Q_3$.

• Черта внутри прямоугольника соответствует 50% персентили (медиане).

• "Усы" строятся слева и справа от "ящика" строятся как линия, покрывающая интервал $(Q_1-1.5(Q_3-Q_1), Q_3+1.5(Q_3-Q_1))$, при этом границы интервала должны лежать на ближайших реальных наблюдениях в данных, поэтому могут выглядеть несимметрично относительно "ящика".

• Наблюдения, выпадающие за границы интервала "усов" визуализируются отдельными точками.

"Ящик" и "усы" могут строиться по другим правилам, если об этом явно говорится в тексте.

Рассмотрим визуализацию распределения аддитивных эффектов для задачи BikeSharing [3], в которой оценивается число сданных напрокат велосипедов в разные дни. Для каждого дня известны его дата, день недели, погода, температура и другие параметры.

На этом же графике можно отложить частные аддитивные эффекты для отдельного прогноза (выделено красным), как показано на рисунке ниже [2]:

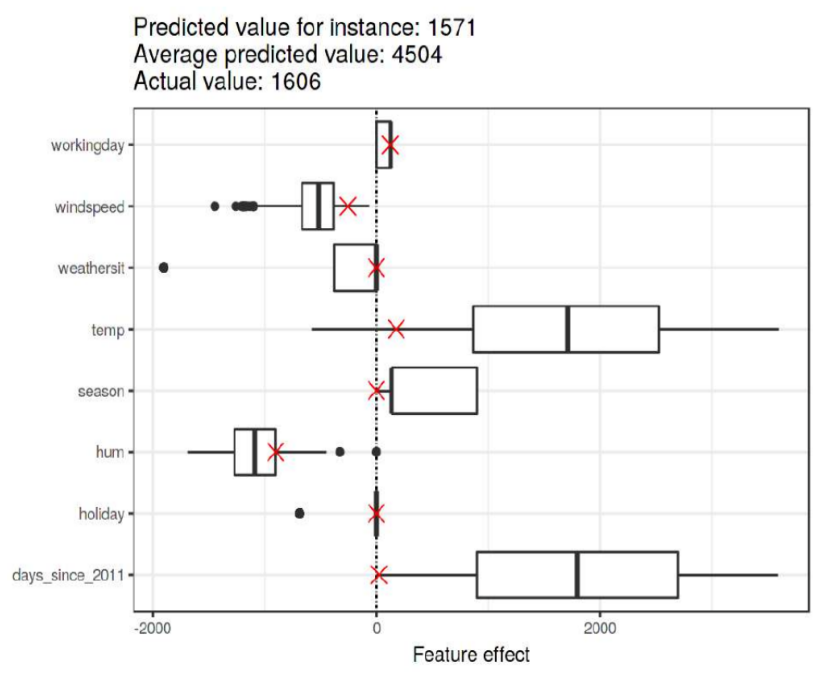
По графику видно, что в целом на аренду велосипедов сильнее всего в плюс влияло время с начала наблюдений (days_since_2011), так как популярность сервиса росла со временем, а также температура дня (temp). А сильнее всего в минус влияла влажность воздуха (hum).

Для аномально низкого прогноза в интересующий день аддитивные эффекты обозначены красными крестиками. Из графика видно, что малый прогноз для выбранного наблюдения основывается на малой температуре, а также на том, что рассматривается аренда в начале наблюдений, когда аренда велосипедов еще не была так популярна.

Снижение числа признаков

Интерпретация даже такой простой модели, как линейная регрессия, может будет затруднена, если число признаков велико, как происходит, например, при работе с текстовыми данными. В этом случае мы можем понять, как каждый отдельно взятый признак влияет на прогноз, но не можем мысленно предсказать прогноз из-за одновременного влияния большого числа других признаков.

Для упрощения интерпретации можно настраивать линейную регрессию с сильной L1-регуляризацией, которая способна отбирать в модель только те признаки, которые сильнее всего влияют на отклик.

Варьируя силу регуляризации (множитель при регуляризаторе), можно заставить модель использовать требуемое небольшое число признаков.

Альтернативно можно использовать OMP-регрессию, отбирающей самые значимые признаки либо использовать другие методы отбора признаков.

Литература

1. Wikipedia: Student's t-test.
2. Molnar C. Interpretable machine learning. – Lulu. com, 2020: linear regression.
3. UC Irvine Machine Learning Repository: Bike Sharing dataset.
4. Wikipedia: box plot.