Регуляризация в линейной регрессии

Идея регуляризации

Как известно, слишком простые (то есть недостаточно гибкие по выразительной способности) модели строят неточные прогнозы из-за недообучения, а слишком сложные (избыточно гибкие) - к неточным прогнозам из-за переобучения, что можно проиллюстрировать характерным графиком:

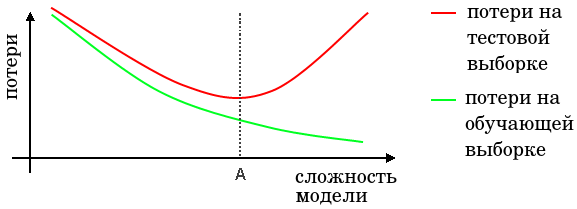
Поэтому важно подобрать сложность модели таким образом, чтобы её сложность соответствовала сложности реальных данных (точка A на графике выше).

Сложность линейной регрессии можно контролировать, варьируя количество признаков, которые мы добавляем в модель, но этот подход обладает следующими недостатками:

• Остаётся неясным, какие признаки удалять в первую очередь?

• Характер влияния будет получаться дискретный, а не непрерывный, что препятствует более тонкой настройке сложности.

• Если все признаки оказывают влияние, то удаление даже части из них будет ухудшать прогноз.

В связи с этими недостатками принято контролировать сложность модели, добавляя в её настройку дополнительное слагаемое (регуляризатор) $R(\mathbf{w})$, как говорилось во введении в регуляризацию:

$$L(\mathbf{w}|X,Y)=\frac{1}{N}\sum_{n=1}^{N}(\mathbf{x}_n^T\mathbf{w} -y_{n})^2+{\color{red}\lambda R(\mathbf{w})} \to \min_\mathbf{w}$$

Популярными способами выбора $R(\mathbf{w})$ являются:

• L2-регуляризация

  $$R(\mathbf{w})=\| \mathbf{w} \|_2^2=\sum_{d=0}^D w_d^2,\quad \text{ вариант: }\,R(\mathbf{w})=\sum_{d={\color{red}1}}^D w_d^2$$

• L1-регуляризация

$$R(\mathbf{w})=\| \mathbf{w} \|_1=\sum_{d=0}^D \vert w_d \vert, \quad \text{ вариант: }\,R(\mathbf{w})=\sum_{d={\color{red}1}}^D |w_d|$$

• ElasticNet-регуляризация

$$R(\mathbf{w})=\alpha \| \mathbf{w} \|_2^2 +(1-\alpha) \| \mathbf{w} \|_1,\quad \alpha\in[0,1]$$

Контроль сложности

Гиперпараметр $\lambda>0$ определяет силу регуляризации, то есть степень упрощения модели. Чем $\lambda$ выше, тем сильнее оптимизатор при настройке весов будет ориентироваться на регуляризатор, прижимающий веса к нулю, а не на точность модели на обучающей выборке. При $\lambda\to\infty$ веса будут стремиться к нулю, а результирующий регрессионный прогноз будет вырождаться в максимально простую модель - константу.

Обратим внимание, что по формулам выше не рекомендуется подвергать регуляризации смещение $w_0$, чтобы даже при слишком сильной регуляризации прогнозы оставались в среднем несмещёнными.

Особенности решения с регуляризацией

Для всех представленных видов регуляризации оптимизируемый критерий будет выпуклым, поэтому, найдя какой-либо минимум, мы можем быть уверены, что это глобальный минимум (докажите).

Линейная регрессия с L2-регуляризацией называется гребневой регрессией (ridge regression), а с L1-регуляризацией - лассо-регрессией (LASSO, Least Absolute Shrinkage and Selection Operator).

Сравнительные достоинства L1- и L2-регуляризации уже рассматривались ранее. Поэтому лишь напомним вкратце, что L1-регуляризация может выдавать оптимальное решение, в котором часть весов будет в точности равна нулю. В контексте линейной регрессии это означает автоматический отбор признаков, поскольку признаки при нулевых коэффициентах вообще не будут оказывать влияния на прогнозы модели. Чем выше гиперпараметр $\lambda$, тем больше признаков будет отброшено из модели.

Анализ данных и интерпретируемость

Коэффициент $\lambda$ полезно варьировать для обнаружения самых значимых признаков для прогнозирования в целях общего анализа данных и интерпретации зависимостей между ними.

L2-регуляризация, в свою очередь, способствует более равномерному распределению весов по признакам и более полному учёту входной информации.

ElasticNet-регуляризация обладает обоими свойствами и требует задания дополнительного гиперпараметра $\alpha\in[0,1]$.

Гиперпараметр $\lambda$ обычно подбирают по прогнозам на валидационной выборке или используя кросс-валидацию по логарифмической сетке значений $[10^{-6},10^{-5},...10^5,10^6]$. Найдя наилучшее значение, его можно уточнить по более мелкой сетке в окрестности найденного значения.

Решение для линейной регрессии с $L_1$- и ElasticNet-регуляризацией находится численными методами, а для гребневой регрессии (L2-регуляризация) его можно найти аналитически.

Будет ли изменение масштаба признаков (после перенастройки модели с новым масштабом) влиять на решение линейной регрессии с регуляризацией?

Да, будет. Например, если признак уменьшим в 100 раз, то соответствующий коэффициент при признаке будет стремиться к увеличению в 100 раз, однако регуляризация не даст в полной мере это реализовать!

Поэтому, чтобы обеспечить регуляризацию одинаковой силы на все признаки, их необходимо предварительно привести к одной шкале, используя нормализацию. Также нормализация важна, если мы хотим выявить самые значимые признаки посредством L1-регуляризации.

Версии линейной регрессии с регуляризациями L1, L2 и ElasticNet реализованы в библиотеке sklearn [1].

Пример запуска в Python

Использование гребневой регрессии:

from sklearn.linear_model import Ridge
from sklearn.metrics import mean_absolute_error

X_train, X_test, Y_train, Y_test = get_demo_regression_data()  
model = Ridge(alpha=1)        # инициализация модели, alpha-вес при регуляризаторе
model.fit(X_train,Y_train)    # обучение модели                
Y_hat = model.predict(X_test) # построение прогнозов
print(f'Средний модуль ошибки (MAE): {mean_absolute_error(Y_test, Y_hat):.2f}')  

Больше информации. Полный код.

Использование LASSO-регрессии:

from sklearn.linear_model import Lasso
from sklearn.metrics import mean_absolute_error

X_train, X_test, Y_train, Y_test = get_demo_regression_data()  
model = Lasso(alpha=1)        # инициализация модели, alpha-вес при регуляризаторе
model.fit(X_train,Y_train)    # обучение модели                
Y_hat = model.predict(X_test) # построение прогнозов
print(f'Средний модуль ошибки (MAE): {mean_absolute_error(Y_test, Y_hat):.2f}')  

Больше информации. Полный код.

Зашумление признаков

Альтернативным способом регуляризации является обучение на признаках, к которым добавлен случайный шум $\mathbf{\delta}\in \mathbb{R}^D$. Это заставит модель не переобучаться под значения отдельных признаков, поскольку значения каждого признака становятся менее надёжными из-за шума. Чем дисперсия шума выше, тем сильнее регуляризующий эффект от зашумления.

Обратим внимание, что при применении модели шум не добавляется. Настроенная модель работает на исходных признаках.

Шум удовлетворяет двум свойствам:

• нулевое мат. ожидание: $\mathbb{E}\mathbf{\delta}=0$,

• нескореллированные компоненты, каждая из которых имеет дисперсию $\lambda$:

$$\text{cov}(\mathbf{\delta})=\mathbb{E}\{\mathbf{\delta}\mathbf{\delta}^T\}=\lambda I,$$

где $I$ - единичная матрица.

Интересно, что если усреднять потери по всевозможным реализациям шума, то получим, что зашумление признаков эквивалентно L2-регуляризации!

Доказательство эквивалентности

$$\begin{aligned} L(\mathbf{w}) &= \mathbb{E} \left\{ \frac{1}{N} \sum_{i=1}^N (y_i - \hat{y}_i)^2 \right\} = \mathbb{E} \left\{ \frac{1}{N} \sum_{i=1}^N (y_i - (\mathbf{x}_i+\mathbf{\delta}_i)^T \mathbf{w})^2 \right\} \\ &= \mathbb{E} \left\{ \frac{1}{N} \sum_{i=1}^N ((y_i - \mathbf{x}_i^T \mathbf{w})-\mathbf{\delta}_i^T \mathbf{w})^2 \right\} \\ &= \mathbb{E} \left\{ \frac{1}{N} \sum_{i=1}^N (y_i - \mathbf{x}_i^T \mathbf{w})^2 - 2 \mathbf{\delta}_i^T \mathbf{w} (y_i - \mathbf{x}_i^T \mathbf{w}) + \mathbf{w}^T \mathbf{\delta}_i \mathbf{\delta}_i^T \mathbf{w} \right\} \\ &= \mathbb{E} \left\{ \frac{1}{N} \sum_{i=1}^N (y_i - \mathbf{x}_i^T \mathbf{w})^2 \right\} - 2 \mathbb{E} \left\{ \mathbf{\delta}_i^T \mathbf{w} (y_i - \mathbf{x}_i^T \mathbf{w}) \right\} + \mathbb{E} \left\{\mathbf{w}^T \mathbf{\delta}_i \mathbf{\delta}_i^T \mathbf{w} \right\} \\ &=\frac{1}{N} \sum_{i=1}^N (y_i - \mathbf{x}_i^T \mathbf{w})^2 + \lambda \|\mathbf{w}\|_2^2, \end{aligned}$$

где в предпоследней формуле мы использовали линейность мат. ожидания, равенство нулю мат. ожидания шума и его известную ковариационную матрицу.

Таким образом, зашумление признаков во время обучения эквивалентно в среднем добавлению L2-регуляризации. О связи зашумления признаков с регуляризацией в более общем случае нелинейных нейросетевых моделей можно прочитать в [1].

Литература

1. Документация sklearn: linear models.

2. Bishop C. M. Training with noise is equivalent to Tikhonov regularization //Neural computation. – 1995. – Т. 7. – №. 1. – С. 108-116.