Нормализация свёрточных слоёв

Для повышения устойчивости и скорости настройки свёрточной нейросети применяется нормализация свёрточных слоёв (convolutional layer normalization).

Эта нормализация несколько отличается от батч-нормализации и нормализации слоя в многослойном персептроне, учитывая специфику обработки пространственных данных на изображениях.

Особенностью свёрточного слоя является то, что свёртка извлекает один и тот же признак в разных локациях на изображении. Таким образом, применив свёртку, мы получаем карту пространственной размерности $H\times W$ значений одного и того же признака, где $H$ - высота, а $W$ - ширина карты признаков. Применив $C$ свёрток, мы получим $H\cdot W$ реализаций каждого из $C$ признаков, извлекаемых каждой свёрткой.

Настройка параметров нейросети производится мини-батчами из $B$ изображений.

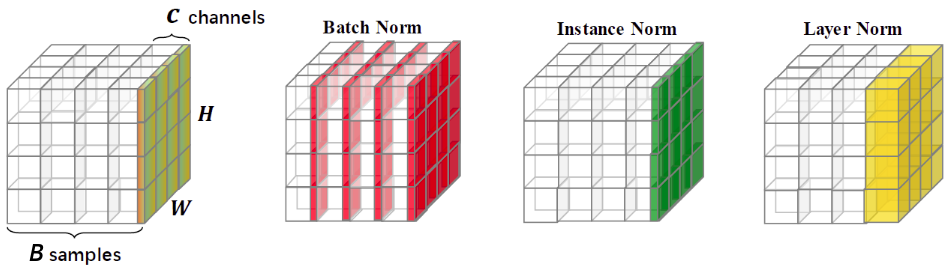
Таким образом, внутреннее представление изображений мини-батча можно представить в виде тензора размера $(B\cdot C)\times H\times W$, как показано на рисунке слева, а основные виды нормализации свёрточных слоёв (batch norm, instance norm, layer norm) - справа [1]:

Каждый тип нормализации задаётся одной и той же формулой, перевзвешивающей активации каналов $1,2,...C$:

$$\begin{aligned} & z_1^b(x,y) \;&\to\quad &\gamma_1\frac{z_1^b(x,y)-\mu_1^b}{\sqrt{(\sigma_1^b)^2+\delta}}+\beta_1, \\ & z_2^b(x,y) \;&\to\quad &\gamma_2\frac{z_2^b(x,y)-\mu_2^b}{\sqrt{(\sigma_2^b)^2+\delta}}+\beta_2, \\ & \cdots & \cdots \\ & z_C^b(x,y) \;&\to\quad &\gamma_C\frac{z_C^b(x,y)-\mu_C^b}{\sqrt{(\sigma_C^b)^2+\delta}}+\beta_C, \\ \end{aligned}$$

где $z_i^b(x,y)$ - активация $i$-й свёртки в позиции $(x,y)$ для изображения $b$ в мини-батче. $\delta=0.001$ - малый параметр, чтобы избежать деления на ноль, а $\gamma_i,\beta_i, i=1,2,...C$ - настраиваемые параметры.

Виды нормализации свёрточных слоёв

Батч-нормализация (batch-normalization [2]) усредняет активации по различным изображениям мини-батча и по различным позициям на каждом изображении:

$$\begin{aligned} \mu_i^b &= \mu_i = \frac{1}{B}\sum_{b=1}^B\frac{1}{HW}\sum_{x=1}^W \sum_{y=1}^H z^b_i(x,y) \\ (\sigma_i^b)^2 &= (\sigma_i)^2 = \frac{1}{B}\sum_{b=1}^B\frac{1}{HW}\sum_{x=1}^W \sum_{y=1}^H (z^b_i(x,y)-\mu_i)^2 \\ \end{aligned}$$

Расчет $\{\mu_i^b,\sigma_i^b\}_{i,b}$ меняется в режимах обучения и применения сети точно так же, как и в обычной батч-нормализации.

Нормализация экземпляра (instance normalization [3]) усредняет независимо для каждого изображения только по его реализациям на различных позициях на изображении:

$$\begin{aligned} \mu_i^b &= \frac{1}{HW}\sum_{x=1}^W \sum_{y=1}^H z^b_i(x,y) \\ (\sigma_i^b)^2 &= \frac{1}{HW}\sum_{x=1}^W \sum_{y=1}^H (z^b_i(x,y)-\mu_i)^2 \\ \end{aligned}$$

Расчет $\{\mu_i^b,\sigma_i^b\}_{i,b}$ не меняется в режимах обучения и применения сети.

Нормализация слоя (layer normalization [4]) усредняет независимо для каждого изображения по всевозможным признакам на всевозможных позициях на изображении:

$$\begin{aligned} \mu_i^b &= \mu^b = \frac{1}{C}\sum_{i=1}^C\frac{1}{HW}\sum_{x=1}^W \sum_{y=1}^H z^b_i(x,y) \\ (\sigma_i^b)^2 &= (\sigma^b)^2 = \frac{1}{C}\sum_{i=1}^C\frac{1}{HW}\sum_{x=1}^W \sum_{y=1}^H (z^b_i(x,y)-\mu_i)^2 \\ \end{aligned}$$

Расчет $\{\mu_i^b,\sigma_i^b\}_{i,b}$ не меняется в режимах обучения и применения сети.

Литература

1. Neupane D., Kim Y., Seok J. Bearing fault detection using scalogram and switchable normalization-based CNN (SN-CNN) //IEEE Access. – 2021. – Т. 9. – С. 88151-88166.
2. Ioffe S., Szegedy C. Batch normalization: Accelerating deep network training by reducing internal covariate shift //International conference on machine learning. – pmlr, 2015. – С. 448-456.
3. Ulyanov D., Vedaldi A., Lempitsky V. Instance normalization: The missing ingredient for fast stylization //arXiv preprint arXiv:1607.08022. – 2016.
4. Ba J. L., Kiros J. R., Hinton G. E. Layer normalization //arXiv preprint arXiv:1607.06450. – 2016.