Перейти к основному содержимому

Автокодировщик

Идея​

Автокодировщик (autoencoder) - это нейросеть x^=f(x)\hat{\mathbf{x}}=f(\mathbf{x}), которой по входу x\mathbf{x} требуется сгенерировать выход x^\hat{\mathbf{x}} максимально похожий на вход. Для настройки автокодировщика обычно используется квадрат L2-потерь:

L(x^,x)=∣∣x^−x∣∣2(1)\mathcal{L}(\hat{\mathbf{x}},\mathbf{x})=||\hat{\mathbf{x}}-\mathbf{x}||^2 \tag{1}
Разметка не используется

Поскольку в качестве целевой переменной (отклика) выступает исходное признаковое описание объекта без меток, то это задача обучения без учителя (unsupervised learning).

Структурно автокодировщик состоит из

  • кодировщика (encoder) e=e(x)\mathbf{e} = e(\mathbf{x})

  • и декодировщика (decoder) d(e)d(\mathbf{e}):

x^=f(x)=d(e(x))\hat{x}=f(x)=d(e(x))

Кодировщик преобразует исходный объект в его внутреннее признаковое представление e\mathbf{e}, называемое эмбеддингом (embedding), а декодировщик пытается по эмбеддингу объекта восстановить исходный объект.

Чтобы избежать тривиального решения задачи, когда автокодировщик настраивается повторять тождественное преобразование x^=x\hat{\mathbf{x}}=\mathbf{x}, на архитектуру / процесс настройки весов накладываются некоторые ограничения, делающие задачу восстановления исходного объекта нетривиальной.

Самый простой случай - потребовать, чтобы размерность эмбеддинга была существенно меньше, чем размерность исходного объекта.

Применения автокодировщика​

  • Предобучение (pretraining). Если для конечной задачи обучения с учителем обучающая выборка {(xn,yn)}n=1N\{(\mathbf{x}_n,y_n)\}_{n=1}^Nмала, но есть много неразмеченных объектов {x}n=1M\{\mathbf{x}\}_{n=1}^M, M≫NM\gg N, то можно на большой неразмеченной выборки настроить автокодировщик f(x)=d(e(x))f(\mathbf{x})=d(e(\mathbf{x})), а потом инициализировать первые слои сети, решающей целевую задачу слоями кодировщика e(x)e(\mathbf{x}), то есть применить трансферное обучение. Таким образом, даже без использования меток мы получим перевод объекта из исходного пространства низкоуровневых признаков x\mathbf{x} в высокоуровневые e(x)e(\mathbf{x}), с которыми проще работать. По сути, кодировщик осуществляет нелинейное снижение размерности признаков (dimensionality reduction), с которыми работает уже прогнозирующая модель.

    При достаточном объёме размеченной выборки можно первые перенесённые слои донастроить под конечную задачу с небольшим шагом обучения (finetuning).

  • Сжатие данных. Если размерность пространства эмбеддингов e(x)e(\mathbf{x}) существенно меньше размерности исходного пространства признаков x\mathbf{x}, то объекты можно хранить не в исходном виде, а в сжатом - в виде эмбеддинга. Чтобы восстановить сжатый объект e(x)e(\mathbf{x}) до исходного, достаточно просто пропустить его через декодировщик x^=d(e(x))\hat{\mathbf{x}}=d(e(\mathbf{x})). Поскольку автокодировщик неидеально восстанавливает исходный объект, получим сжатие данных с потерями (lossy compression), аналогично тому, как изображения хранятся в JPEG-формате.

  • Визуализация данных - частный случай снижения размерности, когда размерность эмбеддинга e(x)e(\mathbf{x}) равна двум или трём. В этом случае сложные многомерные данные можно визуализировать для человека.

  • Фильтрация шума (denoising) достигается за счёт пропускания зашумлённого объекта (например, изображения с шумом) через автокодировщик. Удаление шума обеспечивается тем, что автокодировщик хорошо восстанавливает типичные паттерны реальных данных, которые часто встречаются, а шум случаен, поэтому его сложно воспроизвести. Фильтрующий автокодировщик, описанный далее, специально обучается удалять шум.

  • Детекция аномалий (anomaly detection) - задача, в которой нужно выделить нетипичные объекты, выбивающиеся из общего распределения объектов. Она также может решаться с помощью автокодировщика.

Как с помощью автокодировщика детектировать аномальные объекты?

Автокодировщик настраивается хорошо восстанавливать типичные объекты выборки. Нетипичные объекты имеют нестандартное распределение и встречаются редко, поэтому восстанавливаться автокодировщиком будут плохо. Поэтому о степени аномальности объекта можно судить по ошибке его восстановления:

abnormality(x)=∣∣f(x)−x∣∣2\text{abnormality}(\mathbf{x})=||f(\mathbf{x})-\mathbf{x}||^2

Типы автокодировщиков​

Недоопределённый автокодировщик​

Недоопределённый автокодировщик (undercomplete autoencoder) обладает свойством, что размерность пространства эмбеддингов меньше пространства исходных признаков:

dim(e(x))<dim(x)\text{dim}(e(\mathbf{x}))<\text{dim}(\mathbf{x})

Ниже показан недоопределённый автокодировщик с одним скрытым слоем.

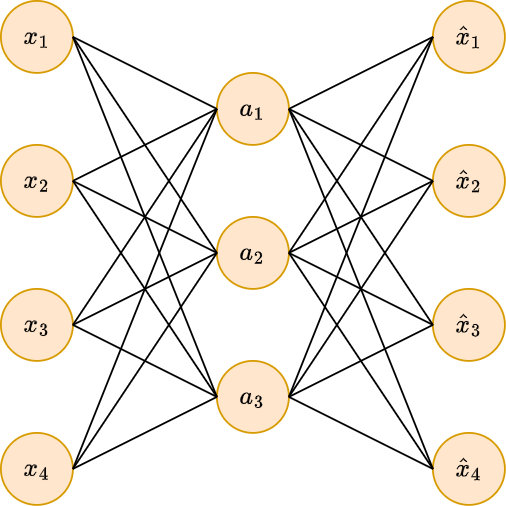
Единичные нейроны здесь и далее опущены для простоты визуализации, но они есть на всех слоях, кроме выходного, чтобы обеспечивать смещение в каждом рассчитываемом нейроне.

Автокодировщик и метод главных компонент

Самым популярным методом линейного снижения размерности (dimensionality reduction) является метод главных компонент (principal component analysis [1]), проецирующий объекты на KK-мерное подпространство наилучшей аппроксимации, т.е. такое пространство, для которого сумма квадратов расстояний между объектами и их проекциями на это подпространство минимально.

Можно показать [2], что недоопределённый автокодировщик с KK нейронами на скрытом слое эквивалентен методу главных компонент, то есть e(x)e(x) выступает проекцией на то же самое подпространство наилучшей аппроксимации, если настройка весов осуществляется согласно (1), а на всех слоях используются тождественные активации.

Больший интерес представляет использование глубокого недоопределённого автокодировщика с нелинейными функциями активации - его кодировочная часть позволяет извлекать нелинейные внутренние признаки (non-linear dimensionality reduction)!

Разреженный автокодировщик​

Разреженный автокодировщик (sparse autoencoder [3]) добивается невырожденного решения (которым выступает тождественное преобразование f(x)=xf(\mathbf{x})=\mathbf{x}) за счёт модификации функции потерь (1), добавляя в неё L1-регуляризацию на эмбеддинг объекта e(x)=[e1,e2,...eK]e(\mathbf{x})=[e_1,e_2,...e_K]:

Ls(x^,x)=∣∣f(x)−x∣∣2+λ∑k=1K∣ek∣,\mathcal{L}_s(\hat{\mathbf{x}},\mathbf{x})=||f(\mathbf{x})-\mathbf{x}||^2+\lambda \sum_{k=1}^K |e_k|,

где λ>0\lambda>0 - гиперпараметр, отвечающий за силу регуляризации. Как и при регуляризации весов модели, использование L1-регуляризации при настройке автокодировщика будет приводить к разреженным эмбеддингам, т.е. эмбеддингам, у которых часть элементов будут в точности равны нулю.

Фильтрующий автокодировщик​

Фильтрующий автокодировщик (denoising autoencoder, [4]) избавляется от вырождения автокодировщика в тождественное преобразование за счёт добавления шума к исходному объекту x\mathbf{x}:

x→+шумx~\mathbf{x} \xrightarrow{\text{+шум}} \tilde{\mathbf{x}}

При этом в функции потерь требуется восстановление исходного незашумлённого объекта x\mathbf{x} по зашумлённому x~\tilde{\mathbf{x}}:

L(x,x^)=∣∣f(x~)−x∣∣2\mathcal{L}(\mathbf{x},\hat{\mathbf{x}})=||f(\tilde{\mathbf{x}})-\mathbf{x}||^2

Шум можно добавлять, зануляя отдельные случайные элементы x\mathbf{x} либо добавляя к x\mathbf{x} Гауссов шум (распределённый по нормальному закону с небольшой дисперсией).

Идеи рассмотренных видов автокодировщиков можно совмещать друг с другом!

Маскированный автокодировщик​

При применении описанного выше фильтрующего автокодировщика к изображениям признаками x\mathbf{x} выступают пиксели изображения, интенсивность которых меняется плавно, из-за чего фильтрующему автокодировщику становится очень просто восстановить зашумлённые пиксели по их соседям.

Чтобы заставить автокодировщик решать более сложную задачу (и получать более интеллектуальные эмбеддинги), можно использовать маскированный автокодировщик (masked autoencoder, [5]), в котором в качестве зашумляющего преобразования применяется исключение не отдельных пикселей, а квадратных фрагментов изображения (патчей, patches), как показано на иллюстрации [5]:

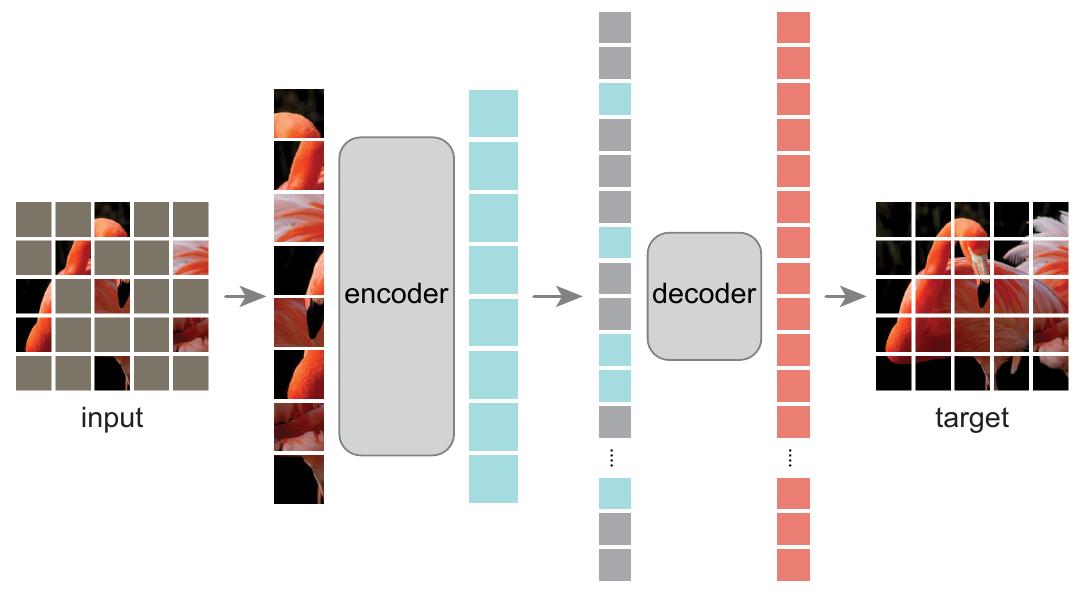
Автокодировщик на базе трансформерной модели (image transformer) позволяет добиться правдоподобного восстановления изображения, даже если 80% фрагментов пропущено [5]:

Сжимающий автокодировщик​

Сжимающий автокодировщик (contractive autoencoder, [6]) аналогичен разреженному автокодировщику, но в качестве регуляризатора используется квадрат нормы Фробениуса от матрицы Якоби (т.е. сумма квадратов элементов матрицы) от эмбеддингов по входным признакам x=[x1,x2,...xD]x=[x^1,x^2,...x^D]:

Lс(x^,x)=∣∣f(x)−x∣∣2+λ∑d=1D∑k=1K(∂ek(x)∂xd)2\mathcal{L}_с(\hat{\mathbf{x}},\mathbf{x})=||f(\mathbf{x})-\mathbf{x}||^2+\lambda \sum_{d=1}^D\sum_{k=1}^K \left( \frac{\partial e_k(\mathbf{x})}{\partial x^d} \right )^2

Таким образом автокодировщик выучивает эмбеддинг, который будет слабо меняться при изменении входа x\mathbf{x}, что заставит вектора эмбеддингов приближаться к низкоразмерному многообразию, описывающему разнообразие реальных многомерных данных.

Вариационный автокодировщик​

Другой популярный вид автокодировщиков - это вариационный автокодировщик (variational autoencoder, VAE [7]), который учится восстанавливать данные таким образом, чтобы распределение эмбеддингов объектов было близко к выбранному априорному распределению (как правило, нормальному), что позволяет обученный автокодировщик использовать не только для сжатия существующих объектов, но и для генерации новых объектов, восстанавливая их из эмбеддингов, сэмплируемых из выбранного распределения.

Детальнее об автокодировщиках можно прочитать в [8] и [9], а вариационный автокодировщик подробно описан в [10].

Литература​

  1. Wikipedia: Метод главных компонент.
  2. Bourlard H. Auto-association by multilayer perceptrons and singular value decomposition. – 2000.
  3. Ranzato M. A. et al. Sparse feature learning for deep belief networks //Advances in neural information processing systems. – 2007. – Т. 20.
  4. Vincent P. et al. Extracting and composing robust features with denoising autoencoders //Proceedings of the 25th international conference on Machine learning. – 2008. – С. 1096-1103.
  5. He K. et al. Masked autoencoders are scalable vision learners //Proceedings of the IEEE/CVF conference on computer vision and pattern recognition. – 2022. – С. 16000-16009.
  6. Rifai S. et al. Contractive auto-encoders: Explicit invariance during feature extraction //Proceedings of the 28th international conference on international conference on machine learning. – 2011. – С. 833-840.
  7. Pham D., Le T. Auto-Encoding Variational Bayes //arXiv preprint arXiv:1312.6114. – 2013.
  8. Bishop C. M., Bishop H. Deep learning: Foundations and concepts. – Springer Nature, 2023.
  9. Goodfellow I. et al. Deep learning. – Cambridge : MIT press, 2016.
  10. Учебник ШАД: Variational Autoencoder (VAE).