Регуляризация весов нейросети

Идея

Вместо того, чтобы жёстко упрощать модель, исключая лишние признаки, нейроны и целые слои, можно упрощать модель мягко, добавляя в функцию потерь регуляризацию, штрафующую веса по их абсолютной величине.

Пусть $X$ - вектора признаков всех объектов обучающей выборки, а Y - вектор их откликов (целевых значений), как вводилось ранее.

Чаще всего используется L2-регуляризация (называемая weight decay):

$$L(X,Y) \to L(X,Y)+\textcolor{red}{\lambda||\mathbf{w}||^2_2} = L(X,Y)+\textcolor{red}{\lambda \sum_{i=1}^I w_i^2}\tag{1}$$

либо $L_1$-регуляризация:

$$L(X,Y) \to L(X,Y)+\textcolor{red}{\lambda||\mathbf{w}||_1} = L(X,Y)+\textcolor{red}{\lambda \sum_{i=1}^I |w_i|}\tag{2}$$

Добавление регуляризующих слагаемых делает оптимальные веса меньше по абсолютной величине, вследствие чего итоговая зависимость $f_\mathbf{w}(\mathbf{x})$ меняется более плавно.

Реальные зависимости тоже в большинстве случаев обладают плавностью изменений, поэтому эти виды регуляризации весьма естественны и при подборе коэффициента $\lambda$ приводят к улучшению обобщающей способности.

Контроль силы регуляризации

Сила регуляризации контролируется гиперпараметром $\lambda>0$: чем он выше, тем сильнее оптимальные веса будут прижаты к нулю и тем более плавную прогнозную функцию мы получим. Важно подвергать модель регуляризации не слишком сильно, иначе её прогнозы могут выродиться в константу!

Обычно $\lambda$ подбирают по качеству модели на отдельной валидационной выборке, перебирая значения по логарифмической сетке, например, $10^{-6},10^{-5},...10^5,10^6$.

Отличия L1- и L2-регуляризаций

Посчитав производную по весу для регуляризаторов в (1) и (2), можно увидеть, что L2-регуляризация сильнее прижимает к нулю большие веса, но слабее - малые. А L1-регуляризация прижимает веса к нулю с одинаковой силой, поскольку градиент по ней - константа.

Поэтому при достаточно большом $\lambda$ L1-регуляризация в точности положит равными нулю часть весов (что эквивалентно удалению соответствующей связи в сети). В то же время при L2-регуляризации все веса будут в общем случае ненулевыми даже при сильной степени регуляризации $\lambda$.

Другим обоснованием, почему L2-регуляризация не зануляет веса, а L1 - зануляет, является эквивалентность следующих задач оптимизации для некоторого порога $\gamma=\gamma(\lambda)$, следующая из условий Каруша-Куна-Таккера [1]:

$$L(\mathbf{w})+\lambda R(\mathbf{w})\to\min_\mathbf{w} \iff \begin{cases} L(\mathbf{w})\to\min_\mathbf{w} \\ R(\mathbf{w})\le\gamma \end{cases}$$

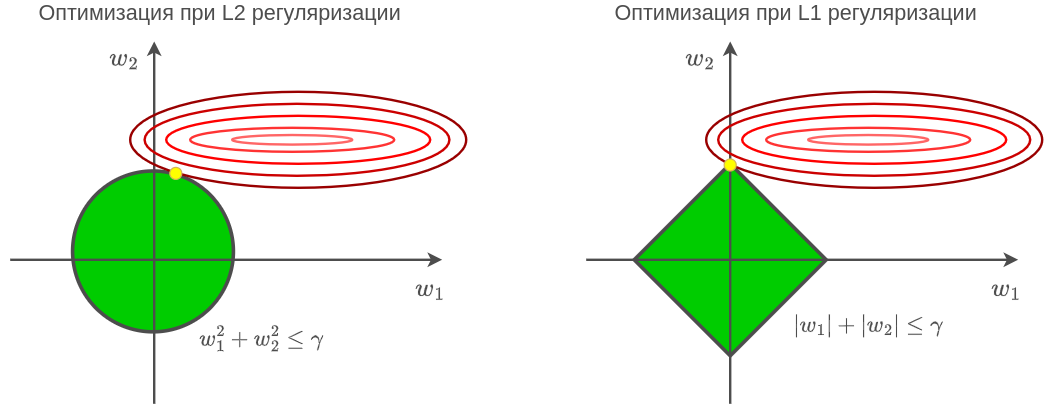
Если визуализировать линии уровня функции потерь и область, задаваемую ограничением второй задачи оптимизации (справа), то видно, что для L2-регуляризации оптимальное значение весов (жёлтый кружок) будет иметь ненулевые веса, а для L1-регуляризации часть оптимальных весов может стать в точности равной нулю:

Особый учёт смещений

Особое значение в нейросети имеют нейроны, принимающие значение тождественной единицы. Веса связей, исходящих из таких нейронов, отвечают за смещения (bias) распределений активаций и обычно не регуляризуются, чтобы регуляризация не приводила к смещению прогнозов в сторону нуля. К тому же весов, отвечающих смещениям, существенно меньше, чем всех прочих, поэтому они не сильно влияют на сложность модели.

Обобщение

Вместо того, чтобы подвергать регуляризации все веса сети с одинаковой силой $\lambda$, можно подвергать регуляризации веса, отвечающие разным слоям сети, с разной силой. Рекомендуется слабее регуляризовать начальные слои, а сильнее - более поздние.

Это объясняется тем, что первые слои сильно связаны со входами $x$, информацию о которых нежелательно потерять из-за чрезмерной регуляризации. В последних же слоях генерируются всевозможные сложные признаки, не все из которых в конечном счёте окажутся полезными.

Литература

1. Wikipedia: Условия Каруша - Куна - Таккера.