Сеть радиально-базисных функций

Определение

Сеть радиально-базисных функций (radial basis function network, RBF-network [1], предложена в [2]) - это специальный вид двухслойной нейронной сети:

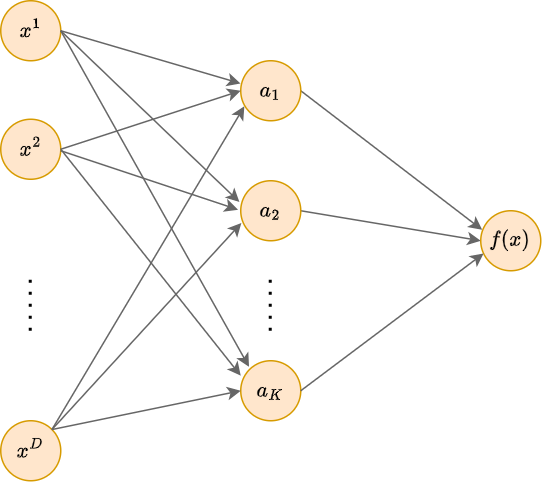
У этой архитектуры отсутствуют смещения (нейроны, выдающие константу 1), а на скрытом слое используются радиальные базисные функции (radial basis function, RBF, RB-функции [3]):

$$a_i=S(||\mathbf{x}-\mathbf{c}_i||),$$

которые зависят только от расстояния между вектором признаков объектом $\mathbf{x}$ и центром $\mathbf{c}_i$. $S(\cdot)\ge 0$ некоторая функция, которая обычно выбирается убывающей, что позволяет трактовать $S(||\mathbf{x}-\mathbf{c}_i||)$ как степень близости $\mathbf{x}$ к $\mathbf{c}_i$ (similarity function).

Прогноз в RBF-сети строится по правилу:

$$f(x)=\sum_{i=1}^K w_i S_i(||\mathbf{x}-\mathbf{c}_i||) \tag{1}$$

В качестве функции близости в (1) чаще всего берётся функция Гауссова ядра (Gaussian kernel):

$$S(||\mathbf{x}-\mathbf{c}||)=e^{-\gamma ||\mathbf{x}-\mathbf{c}||^2_2},$$

где $||\mathbf{x}-\mathbf{c}||^2_2$ - квадрат L2 нормы, то есть квадрат обыкновенного Евклидового расстояния, а $\gamma$ - параметр, характеризующий скорость убывания функции при удалении $\mathbf{x}$ от центра $\mathbf{c}$.

Другими вариантами выбора RB-функции являются обратная квадратичная функция (inverse quadratic):

$$S(||\mathbf{x}-\mathbf{c}||)=\frac{1}{1+\gamma ||\mathbf{x}-\mathbf{c}||^2_2}$$

и обратная мультиквадратичнвая функция (inverse multiquadratic):

$$S(||\mathbf{x}-\mathbf{c}||)=\frac{1}{\sqrt{1+\gamma ||\mathbf{x}-\mathbf{c}||^2_2}},$$

убывающая к нулю более медленно.

С другими популярными видами радиально-базисных функций, в том числе возрастающими, а не только убывающими, можно ознакомиться в [3].

Идеологически RBF-сеть больше всего похожа на метод ближайших центроидов классического машинного обучения, представляя его сглаженную версию, в которой число центроидов не связано напрямую с числом классов, а может быть любым. При этом их расположение не описывается явной формулой, а настраивается автоматически по данным.

Настраиваемые параметры

Настраиваемыми параметрами RBF-сети выступают:

• центры RBF-функций $\mathbf{c}_1,...\mathbf{c}_K$;

• параметры функций близости $\gamma_1,...\gamma_K$;

• веса, с которыми суммируются активации $w_1,...w_K$.

Инициализация параметров

Методы инициализации параметров перед обучением:

• Центры инициализируются случайными объектами выборки.

  • Более устойчивый вариант: инициализировать их центроидами после кластеризации методом K-средних (K-means [4]).

• Коэффициенты $\gamma_1,...\gamma_K$ инициализируются обратной величиной к средним квадратам расстояния между парами объектов, чтобы в начале оптимизации скрытые нейроны имели содержательный и невырожденный характер изменения.

• Веса $w_1,...w_K$ инициализируются случайно.

  • Более устойчивый вариант: как значения откликов в обучающих объектах, ближайших к соответствующим центрам $\mathbf{c}_1,...\mathbf{c}_K$ для случаев, когда RB-функция берётся убывающей от единицы к нулю, и её можно трактовать как функцию близости.

Пример использования

Рассмотрим аппроксимацию следующей модельной функции:

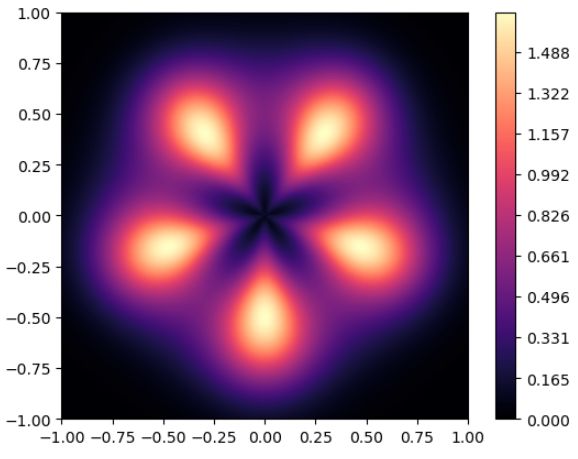
RBF-сеть с тремя центрами может (при некоторой инициализации) моделировать её следующим образом:

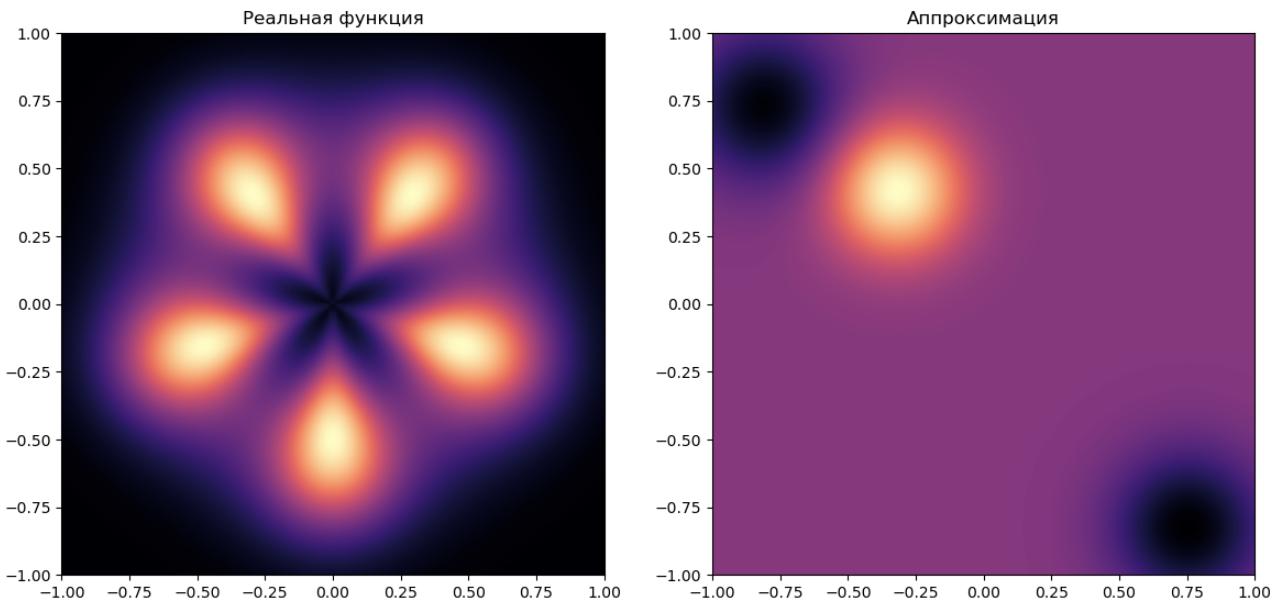
В примере число скрытых нейронов (3 шт.) недостаточно для моделирования всех локальных максимумов функции (5 шт.), и аппроксимация получилась неточной.

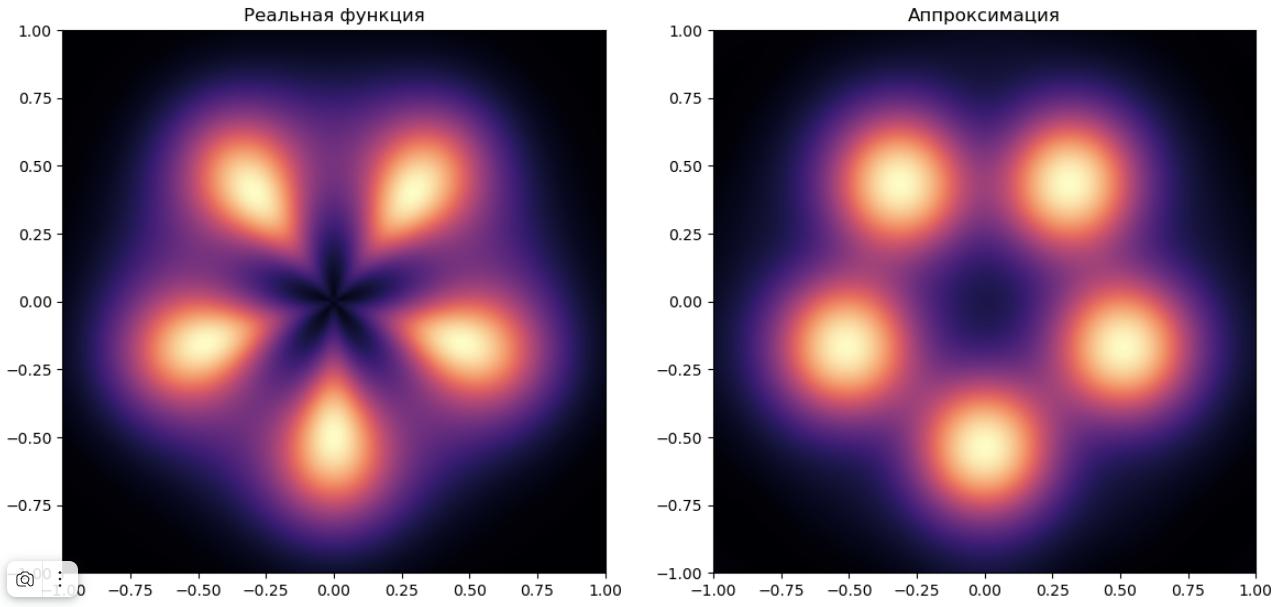
RBF-сеть с 5 центрами:

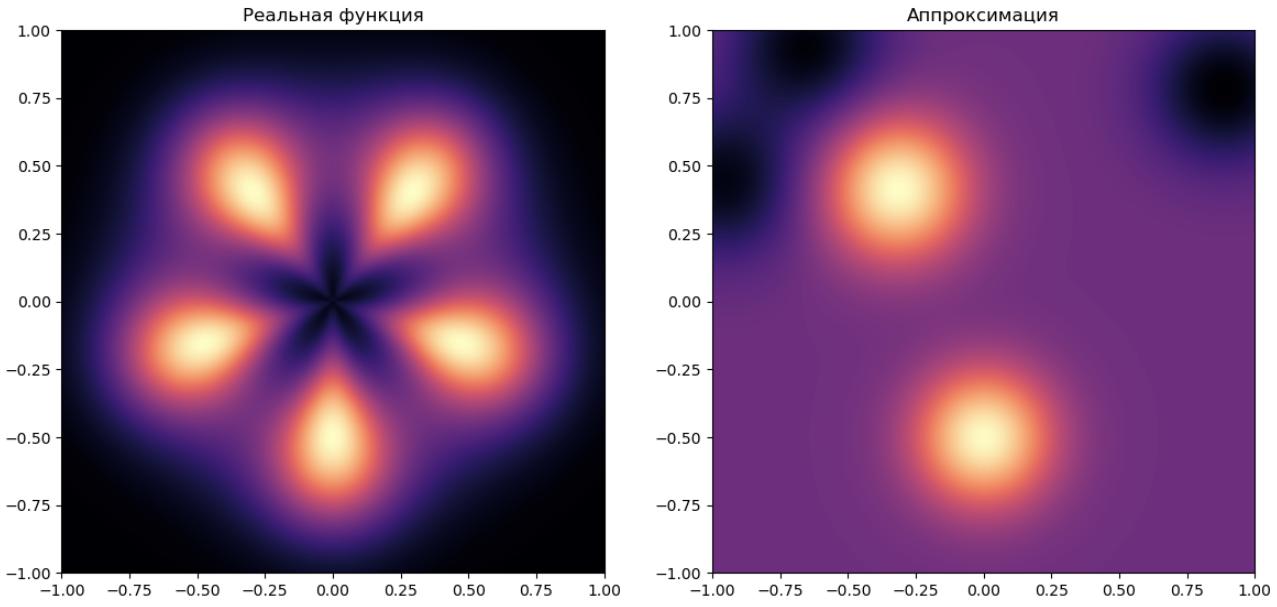
Здесь интересно, что даже в случае, когда число скрытый нейронов совпадает с числом локальных максимумов, аппроксимация всё равно получилась неточной из-за неудачной инициализации центров RB-функций. Часть центров оказалось на периферии моделируемой области, где прогнозируемая функция принимает малые значения. Веса при таких RB-функциях оказались отрицательными.

Вывод: для моделей с малым числом параметров важна грамотная инициализация!

RBF-сеть с 50 центрами будет уже значительно лучше аппроксимировать моделируемую функцию, поскольку при пятидесяти случайных инициализациях хотя бы один центр будет оказываться недалеко от локального максимума:

При дальнейшем наращивании количества RB-функций в скрытом слое точность аппроксимации будет возрастать. В частности, сеть получит возможность моделировать несферическую форму локальных максимумов функции.

Вывод: для повышения точности моделирования лучше выбирать более гибкую перепараметризованную модель и наращивать число обучающих примеров для её точной настройки.

Усложения

Нормализация значений функций близости

Если используются убывающие к нулю RB-функции, такие как Гауссово ядро, то для объектов, расположенных далеко от центров, нейросеть будет выдавать прогнозы, близкие к нулю!

Чтобы при удалении объектов от центров прогнозы сети стремились не к нулю, а константе, рекомендуется добавить смещение (bias) на последнем слое.

Более общее решение - заменить исходные RB-функции на их нормализованные варианты:

$$S_n(||\mathbf{x}-\mathbf{c}_i||) = \frac{S(||\mathbf{x}-\mathbf{c}_i||)}{\sum_{j=1}^K S(||\mathbf{x}-\mathbf{c}_j||)},\quad i=1,2,...K,$$

либо использование возрастающих [3], а не убывающих RB-функций.

Другие функций расстояния

Вместо Евклидового расстояния в (1) можно использовать и другие, например, изученные ранее. В работах [5], [6] расстояние Махаланобиса показало себя лучше Евклидового. Также в сами функции расстояния можно вводить настраиваемые параметры (metric learning).

Совмещение подходов

Классическая модель нейрона с нелинейностью (персептрон), даёт глобальную аппроксимацию данных, изменяющуюся в зависимости от расстояния от объекта $\mathbf{x}$ до гиперплоскости $w_0+\mathbf{w}^T\mathbf{x}$.

Нейрон, основанный на RB-функции, даёт локальную аппроксимацию данных вокруг соответствующего центра $\mathbf{c}_i$. Добавление подобных нейронов к классическую нейросеть позволяет лучше учитывать локальные особенности данных, используя меньшее число параметров.

Пример: почти линейная зависимость с несколькими локальными пиками будет экономичнее моделироваться сочетанием классических нейронов и нейронов, основанных на вычислении RB-функций.

При этом типы нейронов можно совмещать на любом слое сети, а не только на самом первом. Это повышает выразительную способность нейросети, но может приводить к переобучению при отсутствии ярко выраженных локальных особенностей в данных.

---

Дополнительную информацию о применениях радиально-базисных функций можно прочитать в [7].

Литература

1. Wikipedia: Radial basis function network.
2. Lowe D., Broomhead D. Multivariable functional interpolation and adaptive networks //Complex systems. – 1988. – Т. 2. – №. 3. – С. 321-355.
3. Wikipedia: Radial basis function.
4. Wikipedia: k-means clustering.
5. Beheim L. et al. New RBF neural network classifier with optimized hidden neurons number //WSEAS Trans. Syst. – 2004. – Т. 2. – С. 467-472.
6. Ibrikci T. et al. Mahalanobis distance with radial basis function network on protein secondary structures //Proceedings of the Second Joint 24th Annual Conference and the Annual Fall Meeting of the Biomedical Engineering Society. – IEEE, 2002. – Т. 3. – С. 2184-2185.
7. Scholarpedia: Radial basis function.