Перейти к основному содержимому

Рекуррентная сеть

Обработка последовательностей​

Входные данные часто представляются в виде последовательности x1x2...xT\mathbf{x}_1\mathbf{x}_2...\mathbf{x}_T, например:

  • динамика цен на акции,

  • динамика действий посетителя веб-сайта,

  • изменение погоды,

  • текст как последовательность слов,

  • речь как последовательность звуков,

  • видео как последовательность кадров.

Далее для определённости будем рассматривать текст как последовательность слов, подаваемых на вход нейросети в виде эмбеддингов, хотя те же рассуждения применимы и для обработки последовательностей других типов.

Независимая обработка​

Мы могли бы обрабатывать каждый элемент последовательности x\mathbf{x} независимо, используя многослойный персептрон f(x)f(\mathbf{x}):

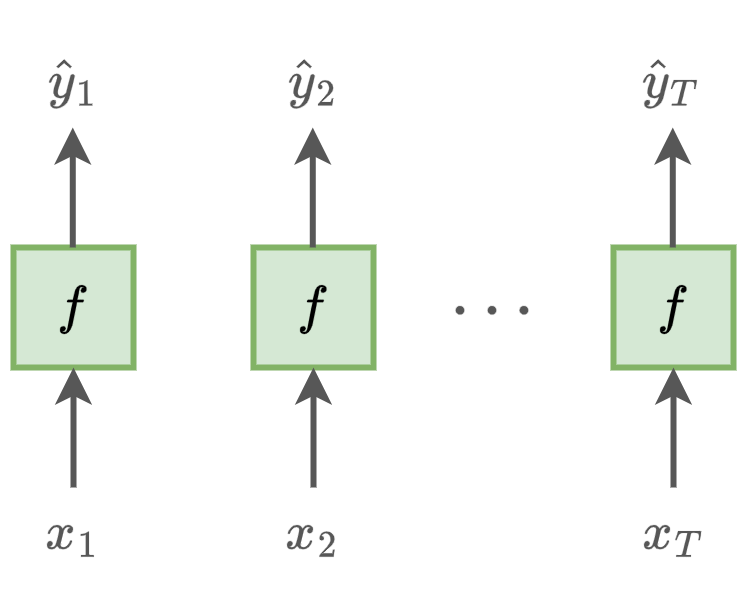
Но такой подход не учитывает зависимости выхода от других элементов последовательности. Например, будущие действия посетителя веб-сайта зависят от его старых действий, динамика будущих цен зависит от их исторических изменений, новые слова текста зависят от старых и т.д.

Проиллюстрируем это примером. Пусть решается задача разметки частей речи для текста (part-of-speech tagging, POS), в которой каждому слову нужно автоматически сопоставить часть речи. Пусть мы обрабатываем фразу "I like to watch movies":

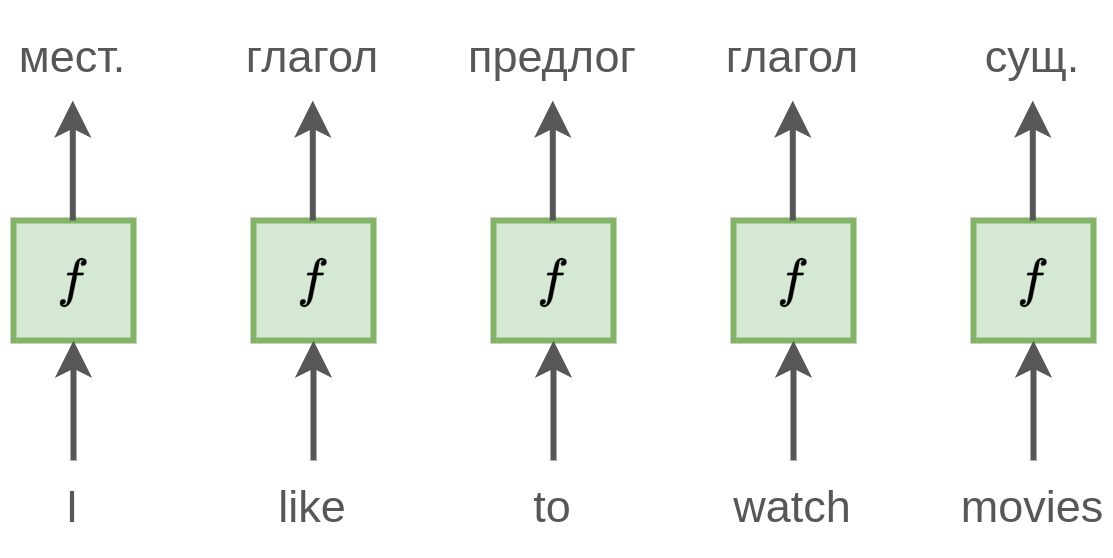
При независимой обработке слов модель будет часто ошибаться, поскольку не учитывает контекст соседних слов, влияющих на роль каждого слова в предложении.

  • [watch] может быть как глаголом, так и существительным, например, во фразе "this is a very expensive watch".

  • [like] также может выступать как существительное, например, во фразе "he gave this post a like".

Если бы модель учитывала предыдущие слова (перед [like] стоит [I], перед [watch] стоит [to]), подобной неоднозначности для неё бы не возникало.

Использование свёрток​

Мы могли бы применить операцию свёртки, чтобы учесть левый контекст:

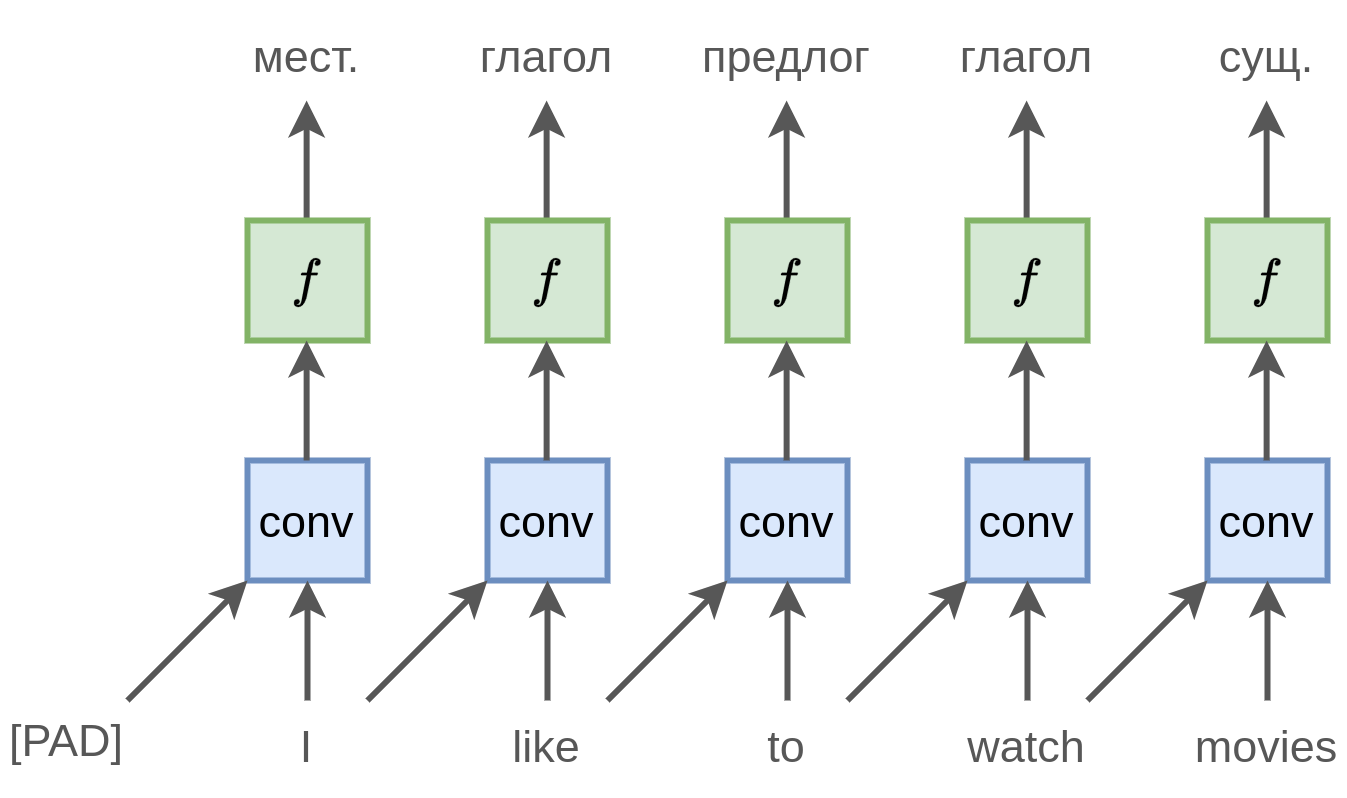
Но тогда был бы учтён контекст, состоящий лишь из одного левого соседа. Часто важен более длинный контекст, например для разрешения неоднозначности слова [watch] во фразе "I like to walk and watch movies".

Для учёта контекста из KK соседей можно было бы применить свёртку с более широким ядром или KK раз применить свёртку с двумерным ядром. Ранее мы уже рассматривали эту идею в свёрточных сетях для обработки последовательностей. Недостатком архитектуры является то, что использование свёрток приводит к обработке, учитывающей лишь ограниченный контекст.

Рекуррентные сети​

Учитывая перечисленные недостатки, для анализа и обработки последовательностей чаще используются рекуррентные нейросети (Recurrent neural net, RNN), способные помнить (в теории) весь исторический контекст из предыдущих наблюдений и учитывать его вычислительно эффективно.

Для этого используется скрытое состояние (hidden state) ht∈RDh\mathbf{h}_t\in\mathbb{R}^{D_h}, хранящее контекст из всех ранее виденных наблюдений. Прогноз строится, учитывая не только текущее наблюдение xt\mathbf{x}_t, но и ht\mathbf{h}_t, что обеспечивает зависимость прогноза от всей истории наблюдений:

y^t=f(xt,ht)\hat{\mathbf{y}}_t = f(\mathbf{x}_t, \mathbf{h}_t)

y^t\hat{y}_t часто не является итоговым прогнозом, а представляет собой лишь промежуточный эмбеддинг, к которому уже применяется многослойный персептрон для получения итогового прогноза.

Само скрытое состояние пересчитывается на каждом шаге обработки последовательности рекуррентно по текущему наблюдению и своему значению на предыдущем шаге обработки:

ht=g(xt,ht−1),t=1,2,3,...\mathbf{h}_t=g(\mathbf{x}_t, \mathbf{h}_{t-1}), \quad t=1,2,3,...

Последовательный процесс генерации прогнозов y^1,y^2,...y^T\hat{\mathbf{y}}_1,\hat{\mathbf{y}}_2,...\hat{\mathbf{y}}_T по входам x1,x2,...xT\mathbf{x}_1,\mathbf{x}_2,...\mathbf{x}_T

и скрытым состояниям можно графически представить так:

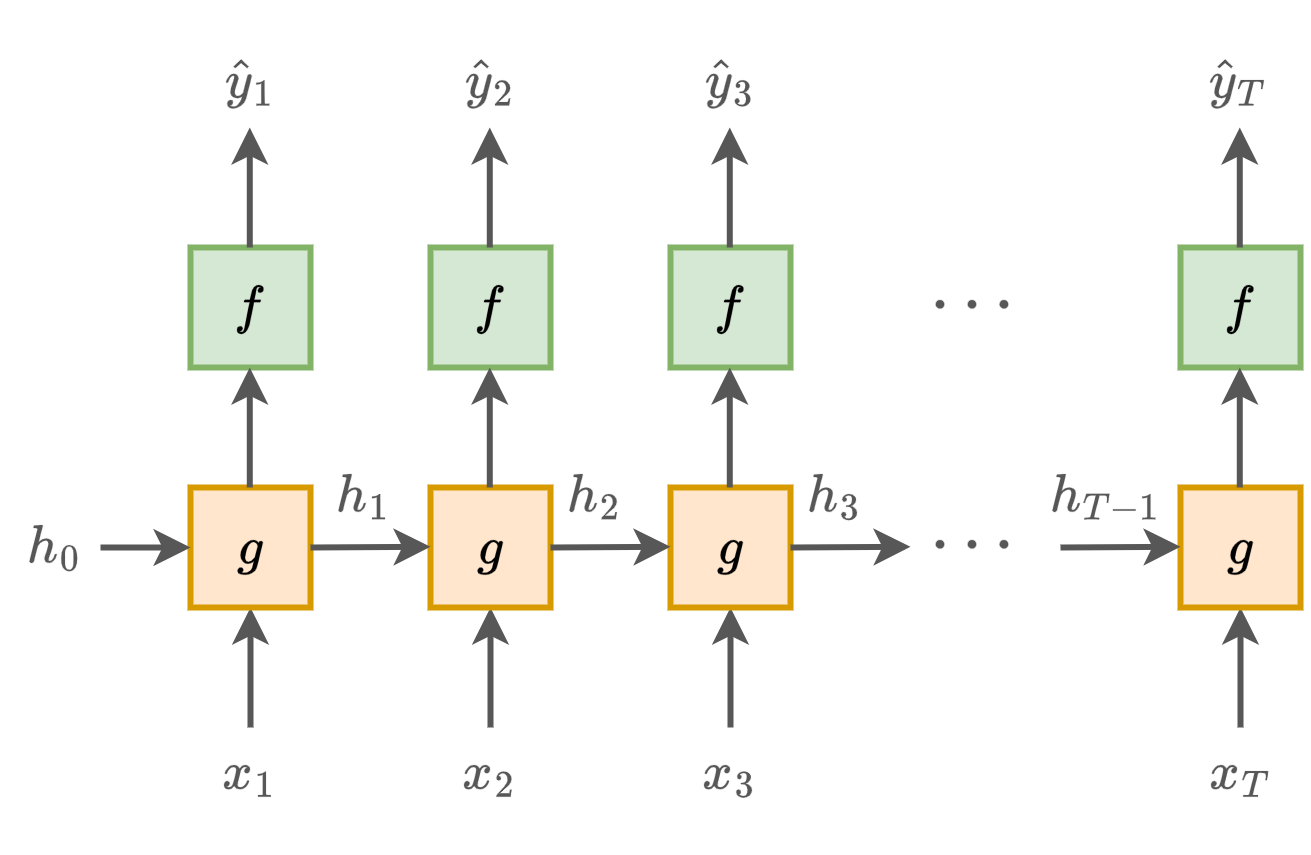
При этом h0∈RDh\mathbf{h}_0\in\mathbb{R}^{D_h} - тоже параметр сети, который можно задавать вектором из нулей или настраивать по данным.

Если разворачивать зависимость рекуррентной сети (network unfolding)

y^t=f(ht)=f(g(xt,ht−1))=f(g(xt,g(xt−1,ht−2)))==f(g(xt,g(xt−1,g(xt−2,ht−3))))=...=F(xt,xt−1,...x1,h0),\widehat{\mathbf{y}}_{t}=f(\mathbf{h}_{t})=f(g(\mathbf{x}_{t},\mathbf{h}_{t-1}))=f(g(\mathbf{x}_{t},g(\mathbf{x}_{t-1},\mathbf{h}_{t-2})))=\\=f(g(\mathbf{x}_{t},g(\mathbf{x}_{t-1},g(\mathbf{x}_{t-2},\mathbf{h}_{t-3}))))=...=F(\mathbf{x}_{t},\mathbf{x}_{t-1},...\mathbf{x}_{1},\mathbf{h}_{0}),

то можно увидеть, что y^t\hat{\mathbf{y}}_t зависит от всех ранее виденных наблюдений xt,xt−1,...x1\mathbf{x}_{t},\mathbf{x}_{t-1},...\mathbf{x}_{1} и строится многократным применением одних и тех же преобразований g(⋅),f(⋅)g(\cdot),f(\cdot), просто применённых к различным входным данным.

Таким образом, рекуррентная сеть - это обычная многослойная сеть, имеющая на каждом слое одинаковые параметры (weight sharing), а число слоёв пропорционально номеру обрабатываемого элемента последовательности tt. То есть для длинного входа эта сеть может содержать очень большое число слоёв.

Проблемы настройки​

Из-за того, что число слоёв велико, а параметры сети одни и те же на каждом слое, настройка рекуррентной сети довольно неустойчива и имеет тенденцию скатываться в одну из крайностей:

  • сеть экспоненциально быстро забывает историю (проблема затухающих градиентов, vanishing gradient problem);

  • сеть экспоненциально быстро увеличивает вклад дальних наблюдений в прогноз, вследствие чего прогноз и настройка весов ведут себя неустойчиво (проблема взрывающихся градиентов, exploding gradient problem).

Для решения первой проблемы используются специальные архитектуры, такие как GRU и LSTM.

Для решения второй используется обрезка градиентов (gradient clipping) по абсолютному или относительному значению.

Простейшая рекуррентная сеть​

Простейшей рекуррентной сетью является сеть Элмана [1]:

ht=g(Wxhxt+Whhht−1+bh),y^t=f(Whyht+by),\begin{aligned} \mathbf{h}_{t} & =g\left(W_{xh}\mathbf{x}_{t}+W_{hh}\mathbf{h}_{t-1}+\mathbf{b}_{h}\right),\\ \widehat{\mathbf{y}}_{t} & =f\left(W_{hy}\mathbf{h}_{t}+\mathbf{b}_{y}\right), \end{aligned}

где

  • g(⋅),f(⋅)g(\cdot),f(\cdot) - некоторые функции нелинейности;

  • Wxh,Whh,WhyW_{xh},W_{hh},W_{hy} - обучаемые матрицы;

  • bh,by\mathbf{b}_h,\mathbf{b}_y - обучаемые вектора смещений.

Настройка рекуррентной сети​

Для эффективного использования возможностей параллелизации на видеокарте, рекуррентная сеть синхронно обрабатывает не одну последовательность, а сразу минибатч из BB последовательностей.

Для этого вычисления переписываются в матричной форме, что для сети Элмана будет иметь следующий вид:

Ht=g(WxhXt+WhhHt−1+bheT),Y^t=f(WhyHt+byeT),\begin{aligned}H_{t} & =g\left(W_{xh}X_{t}+W_{hh}H_{t-1}+\mathbf{b}_{h}\mathbf{e}^T\right),\\ \widehat{Y}_{t} & =f\left(W_{hy}H_{t}+\mathbf{b}_{y}\mathbf{e}^T\right), \end{aligned}

где

  • Xt∈RD×BX_t\in\mathbb{R}^{D\times B} - матрица текущих входов для каждой последовательности (по столбцам);

  • Ht∈RD×BH_t\in\mathbb{R}^{D\times B} - матрица текущих состояний для каждой последовательности (по столбцам);

  • e=[1,1,...,1]T∈RB\mathbf{e}=[1,1,...,1]^T\in\mathbb{R}^B - вектор из единиц, домножение на который повторяет вектор смещения BB раз.

Для обучения по минибатчам, последовательности должны быть одинаковой длины TT.

Обработка коротких последовательностей​

Если входная последовательность короче TT, то она дополняется спец. токеном [PAD], обозначающим пустой вход. Например, при T=7T=7 и входной последовательности "I like to watch movies", она будет преобразована в [[I], [like], [to], [watch], [movies], [pad], [pad]].

Опционально перед первым [PAD] может ставиться спец. токен [EOS], чтобы в явном виде обозначить конец ввода.

Для того, чтобы как можно меньше операций производить вхолостую, обрабатывая пустой токен [PAD], входные последовательности предварительно сортируются по числу элементов и обрабатываются блоками из последовательностей примерно одинаковой длины, как показано ниже:

На рисунке зелёным обозначены реальные токены последовательности, а жёлтым - дополнение токеном [PAD].

Настройка сети производится по развернутой рекуррентной сети (unfolded network), когда явно выписана зависимость между выходом и всеми входами. Этот способ настройки называется обратным распространением ошибки во времени (back propagation through time, BPTT) [2].

Обработка длинных последовательностей​

Если входная последовательность слишком длинная, то прямой и обратный проход в методе обратного распространения ошибки могут не поместиться в память. В этом случае разворачивание применяется не до самого начала входной последовательности, а не более, чем на KK шагов назад. Этот метод называется обрезанным распространением ошибки во времени (truncated back propagation through time, truncated BPTT).

В этом методе сначала обрабатывается первый блок входов x1x2...xK\mathbf{x}_1\mathbf{x}_2...\mathbf{x}_K, получая итоговое скрытое состояние hK\mathbf{h}_K и выходы y^1y^2...y^K\hat{\mathbf{y}}_1\hat{\mathbf{y}}_2...\hat{\mathbf{y}}_K, по которым считаются потери и проходит одна итерация градиентного метода оптимизации. Далее из состояния hK\mathbf{h}_K и входов xK+1xK+2...x2K\mathbf{x}_{K+1} \mathbf{x}_{K+2} ... \mathbf{x}_{2K} генерируется новое скрытое состояние h2K\mathbf{h}_{2K} и выходы y^K+1y^K+2...y^2K\hat{\mathbf{y}}_{K+1}\hat{\mathbf{y}}_{K+2}...\hat{\mathbf{y}}_{2K}, по которым снова считаются ошибки и уточняются параметры сети. Так процесс продолжается, пока не будет обработана вся длинная последовательность целиком.

Особенность truncated BPTT

Обратим внимание, что truncated BPTT не позволяет процессу оптимизации учитывать зависимости длиннее, чем на KK шагов назад. Это препятствует учёту долгосрочных зависимостей. Но на это можно смотреть и как на регуляризатор, в явном виде не позволяющий модели переобучаться под зависимости, которые слишком растянуты во времени и могут оказаться ложными (false dependencies). Также это делает настройку сети более стабильной, уменьшая проблему взрывающихся градиентов (exploding gradient problem), которая тем сильнее, чем большим числом слоёв производится обработка входной последовательности.

С обработкой длинных последовательностей приходится иметь дело, например, в задаче языкового моделирования, когда требуется предсказывать следующее слово по предыдущим, обучаясь на длинных текстах.

Обучение сети строится следующим образом:

  1. Собирается большое число текстов, которые объединяются в одну большую последовательность, разделённую токенами [EOS] (end of sequence).

  2. Далее рекуррентная сеть проходит по всей последовательности, и сохраняются скрытые состояния на каждом шаге.

  3. Формирование минибатчей обучающих последовательностей происходит нарезкой объединённой ппоследовательности либо на последовательные блоки, либо на случайные длины TT.

Регуляризация​

Для борьбы с переобучением при настройке сети используется регуляризация любым из ранее изученных методов: можно ограничивать число слоёв и нейронов, накладывать L1/L2L_1/L_2-регуляризацию на веса, использовать аугментацию и другие приёмы.

Трансферное обучение​

При обработке текстов рекуррентными сетями слова представляются эмбеддингами. Поскольку уникальных слов много, то, чтобы упростить настройку модели, эмбеддинги слов можно брать из другой задачи, используя трансферное обучение. Например, из метода LSA, применённого к матрице совстречаемости слов либо из языковой модели (language model) Word2vec или FastText. Однако поскольку эмбеддинги слов - это точно такие же параметры модели, как и веса самой рекуррентной сети, то при достаточном объёме обучающей выборки их можно настраивать вместе с самой моделью или дообучать под конечную задачу.

Учёт редких и новых слов​

Для того, чтобы сократить число обучаемых эмбеддингов слов, можно заменить редко встречающиеся слова (например, меньше трёх раз во всех документах) специальным токеном [unknown].

Помимо существенного сокращения числа выучиваемых параметров (поскольку в языке очень много редких слов, согласно закону Ципфа [3]), это дополнительно позволит модели органично обрабатывать новые слова во время применения на тестовой выборке, - их достаточно также заменить токеном [unknown]!

:::

DropOut в рекуррентных сетях​

Рассмотрим особенности применения DropOut-регуляризации в рекуррентных сетях.

Случайное отбрасывание нейронов вдоль оси времени (вдоль итераций обработки последовательности) разрывает зависимости между последовательными наблюдениями, что препятствует настройке сети на учёт временных зависимостей. Поэтому в [3] предложено применять DropOut только между слоями многоуровневой обработки данных (naive RNN DropOut). В этом методе случайно отбрасываются нейроны, отвечающие за преобразования xt→ht\mathbf{x}_t \to \mathbf{h}_t и ht→yt\mathbf{h}_t\to\mathbf{y}_t, но все нейроны, отвечающие за зависимость ht−1→ht\mathbf{h}_{t-1} \to \mathbf{h}_{t}, остаются нетронутыми.

В [4] предложено накладывать DropOut не только вдоль уровней обработки, но и вдоль оси времени (итераций обработки), при этом для каждой последовательности генерировать и фиксировать одну и ту же маску для вертикальных и горизонтальных связей (variational RNN DropOut).

Оба способа проиллюстрированы ниже [4], где пунктиром обозначены переходы без отбрасывания нейронов, а сплошной линией - слои с DropOut, использующей DropOut-маску прореживания нейронов, обозначенную цветом (одному цвету отвечает одинаковая маска):

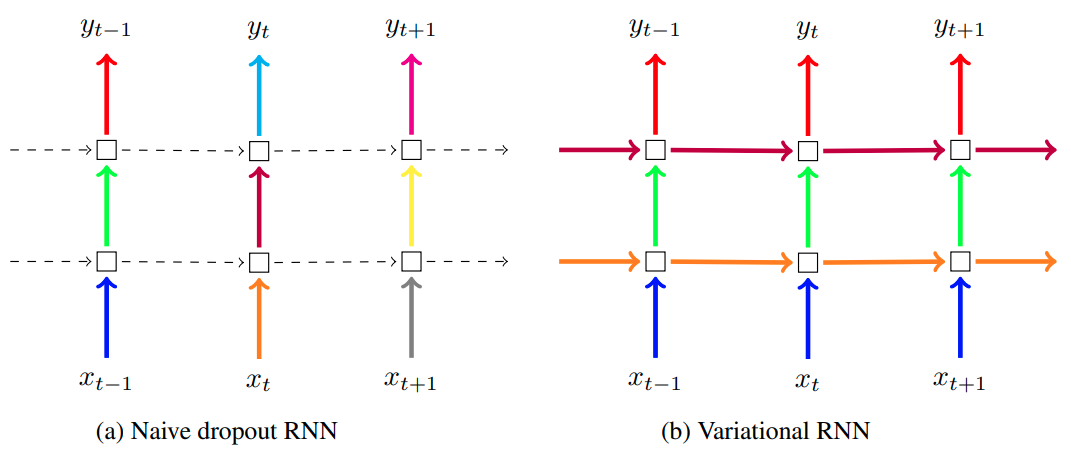
Использование одной и той же маски прореживания вдоль итераций обработки позволяет применять DropOut-регуляризацию, оставляя модели возможность учитывать долгосрочные зависимости между наблюдениями через сохранённые нейроны.

Входы и выходы рекуррентной сети​

Если вход вещественный xt∈RD\mathbf{x}_t\in\mathbb{R}^D (например, вектор текущих цен на выбранные акции на бирже), то он и используется как вход. Аналогично, если вещественный выход yt∈RK\mathbf{y}_t\in\mathbb{R}^K (например, вектор будущих цен на акции), то он тоже напрямую используется как выход (но его можно использовать и как промежуточный эмбеддинг, служащий входом для другой модели, такой как многослойный персептрон).

Если вход категориальный (принадлежит одной из CinC_{in} дискретных категорий), как, например, слово языка, то каждая категория кодируется своим DD-мерным эмбеддингом (вектором вещественных чисел), и вместо категории в качестве xt\mathbf{x}_t подаётся соответствующий ей эмбеддинг. Как мы видели, эмбеддинги могут заимствоваться из другой задачи, используя трансферное обучение. Например, для кодировки слов можно использовать Word2Vec, обученный решать задачу языкового моделирования. В качестве альтернативы (если обучающая выборка достаточно велика) можно обучать эмбеддинги под итоговую задачу вместе с остальными параметрами рекуррентной сети. В качестве инициализации такого обучения также можно подставлять эмбеддинги, полученные из другой задачи.

Если категорий мало, например, при обработке текста не пословно, а посимвольно, в качестве эмбеддингов допускается использовать one-hot кодирование.

Если выход категориальный (принадлежит одной из CoutC_{out} дискретных категорий), то выходом рекуррентной сети служит вектор из CoutC_{out} вещественных чисел, трактуемых как рейтинги соответствующих категорий. К этим рейтингам применяется SoftMax-преобразование, чтобы получить вероятности категорий. Итоговую категорию можно выбирать как самую вероятную либо сэмплировать её согласно предсказанному распределению.

Последнее полезно, например, в задаче генерации языка, когда по предыдущим словам нужно генерировать следующее. Если всегда брать самое вероятное слово, то сгенерированный текст будет получаться слишком однообразным.

Рекуррентная сеть как кодировщик​

Обратим внимание, что, пройдя по всей последовательности, рекуррентная сеть в последнем скрытом состоянии (а также на последнем выходе, если он векторный) хранит эмбеддинг этой последовательности, кодирующий всю последовательность вектором фиксированной длины.

В частности, можно получить:

  • эмбеддинг слова, пройдя по нему как по последовательности букв;

  • эмбеддинг параграфа, пройдя по нему как по последовательности слов;

  • эмбеддинг звука, пройдя по нему как по последовательности частот;

  • эмбеддинг видео, пройдя по нему как по последовательности кадров.

Эмбеддинг последовательности можно далее использовать как входной вектор признаков для многослойного персептрона, решающего конечную задачу (например, классификации комментариев на положительные и отрицательные). Настраивать веса рекуррентной сети нужно вместе с весами модели, использующей полученные эмбеддинги.

Далее мы изучим, как использовать рекуррентную сеть, чтобы генерировать последовательности, например, последовательности слов в тексте, как оценивать качество полученных языковых моделей, как повысить качество генерации с помощью лучевого поиска, рассмотрим режимы применения рекуррентных нейронных сетей, а также усложнения их архитектуры. В конце изучим популярные продвинутые версии рекуррентных сетей - модели LSTM и GRU, которые позволяют более эффективно помнить и использовать более ранние наблюдения.

Литература​

  1. Elman J. L. Finding structure in time //Cognitive science. – 1990. – Т. 14. – №. 2. – С. 179-211.
  2. Werbos P. J. Backpropagation through time: what it does and how to do it //Proceedings of the IEEE. – 1990. – Т. 78. – №. 10. – С. 1550-1560.
  3. Wikipedia: Закон Ципфа.
  4. Wojciech Zaremba, Ilya Sutskever, and Oriol Vinyals. Recurrent neural network regularization. arXiv:1409.2329, 2014.
  5. Gal Y., Ghahramani Z. A Theoretically Grounded Application of Dropout in Recurrent Neural Networks, arXiv e-prints, p //arXiv preprint arXiv:1512.05287. – 2015.