Алгоритм градиентного бустинга

Базовый алгоритм

Разобравшись в идее построения каждой следующей базовой модели в градиентном бустинге, приходим к следующему алгоритму построения итогового ансамбля:

Алгоритм градиентного бустинга

Вход:

• обучающая выборка $X,Y=\left\{ (\mathbf{x}_{n},y_{n})\right\} _{n=1}^{N}$ ;

• функция потерь $\mathcal{L}(f,y)$ и число базовых моделей $M$.

---

1. Настраиваем начальное приближение $G_{0}(\mathbf{x})$ по $X,Y$.

2. Для каждого $m=1,2,...M$:

   1. вычисляем градиенты: $g_{n}=\frac{\partial\mathcal{L}(G_{m-1}(\mathbf{x}_{n}),y_{n})}{\partial G};$

   2. настраиваем $f_{m}(\cdot)$ на выборке $\{(\mathbf{x}_{n},-g_{n})\}_{n=1}^{N}$;

   3. обновляем $G_{m}(\mathbf{x})=G_{m-1}(\mathbf{x})+\varepsilon f_{m}(\mathbf{x})$.

---

Выход: композиция $G_{M}(\mathbf{x})$.

Алгоритм с переменным шагом

Шаг обучения $\varepsilon$ можно варьировать, подбирая его наилучшее значение на каждой итерации, решая задачу одномерной оптимизации (например, простым перебором по сетке):

Алгоритм градиентного бустинга с адаптацией шага обучения

Вход:

• обучающая выборка $X,Y=\left\{ (\mathbf{x}_{n},y_{n})\right\} _{n=1}^{N}$ ;

• функция потерь $\mathcal{L}(f,y)$ и число базовых моделей $M$.

---

1. Настраиваем начальное приближение $G_{0}(\mathbf{x})$ по $X,Y$.

2. Для каждого $m=1,2,...M$:

   1. вычисляем градиенты: $g_{n}=\frac{\partial\mathcal{L}(G_{m-1}(\mathbf{x}_{n}),y_{n})}{\partial G};$

   2. настраиваем $f_{m}(\cdot)$ на выборке $\{(\mathbf{x}_{n},-g_{n})\}_{n=1}^{N}$;

   3. настраиваем шаг $\varepsilon_{m}=\arg\min_{\varepsilon>0}\sum_{n=1}^{N}\mathcal{L}\left(G_{m-1}(\mathbf{x}_{n})+\varepsilon f_{m}(\mathbf{x}_{n}),y_{n}\right);$

   4. обновляем $G_{m}(\mathbf{x})=G_{m-1}(\mathbf{x})+\varepsilon_{m} f_{m}(\mathbf{x}).$

---

Выход: композиция $G_{M}(\mathbf{x})$.

Модификация для решающих деревьев

Когда базовыми алгоритмами $f_1(\mathbf{x}),...f_M(\mathbf{x})$ выступают решающие деревья (что и применяется почти всегда на практике), то алгоритм немного изменяется. Как известно, решающее дерево разбивает пространство признаков на систему непересекающихся прямоугольников $R_1,...R_K$, соответствующих листьям дерева. Каждому листу $k=1,2,...K$ (и соответствующему прямоугольнику) назначается константный прогноз $\gamma_k$, как показано на иллюстрации:

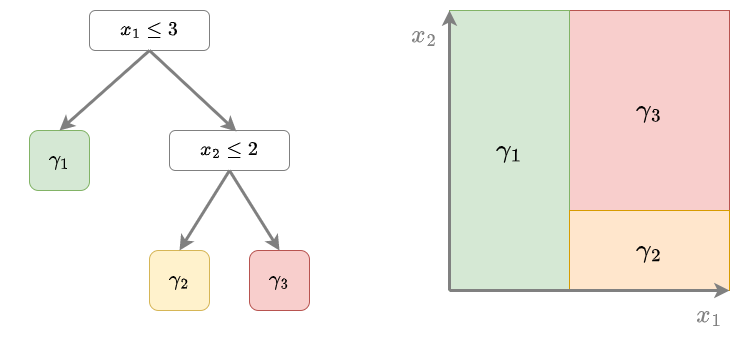
Прогноз решающего дерева имеет вид:

$$\hat{y}(\mathbf{x}) = \sum_{k=1}^K \gamma_k \mathbb{I}[\mathbf{x}\in R_k]$$

После настройки решающего дерева на шаге 2.ii, предлагается индивидуально подобрать прогнозы $\gamma_1,...\gamma_K$ для каждой соответствующей области признакового пространства, чтобы они лучше всего улучшили качество работы ансамбля:

Алгоритм градиентного бустинга для решающих деревьев

Вход:

• обучающая выборка $X,Y=\left\{ (\mathbf{x}_{n},y_{n})\right\} _{n=1}^{N}$;

• функция потерь $\mathcal{L}(f,y)$ и число базовых моделей $M$.

---

1. Настраиваем начальное приближение $G_{0}(\mathbf{x})$ по $X,Y$.

2. Для каждого $m=1,2,...M$:

   1. вычисляем градиенты: $g_{n}=\frac{\partial\mathcal{L}(G_{m-1}(\mathbf{x}_{n}),y_{n})}{\partial G}$;

   2. настраиваем решающее дерево $f_{m}(\cdot)$ на выборке $\{(\mathbf{x}_{n},-g_{n})\}_{n=1}^{N}$, получаем разбиение пространства признаков $\{R_{k}\}_{k=1}^{K}$;

   3. для каждого прямоугольника $R_{k}$ $(k=1,2,...K)$ пересчитываем прогнозы:

      $$\gamma_{k}=\arg\min_{\gamma}\sum_{\mathbf{x}_{n}\in R_{k}}\mathcal{L}(F_{m-1}(\mathbf{x}_{n})+\gamma,\,y_{n})$$

   4. обновляем $G_{m}(\mathbf{x}):=G_{m-1}(\mathbf{x}) + \sum_{k=1}^{K}\gamma_{k}\mathbb{I}[\mathbf{x}\in R_{k}]$.

---

Выход: композиция $G_{M}(\mathbf{x})$.

Обратим внимание, что в этой схеме отсутствует подбор коэффициента $\varepsilon_m$ при базовой модели. Учёт коэффициента мог бы синхронно изменять все прогнозы добавляемого решающего дерева в каждом прямоугольнике. Но необходимости в этом нет, поскольку мы уже подобрали индивидуальные прогнозы в каждом прямоугольнике на шаге 2.iii.

Также с реализацией градиентного бустинга и особенностью реализации для решающих деревьев можно ознакомиться в [1].

Пример запуска на Python

Градиентный бустинг для классификации:

from sklearn.ensemble import GradientBoostingClassifier
from sklearn.metrics import accuracy_score
from sklearn.metrics import brier_score_loss

X_train, X_test, Y_train, Y_test = get_demo_classification_data()  

# инициализация модели (базовые модели-по умолчанию деревья, но могут быть другие):
model = GradientBoostingClassifier(n_estimators=1000,  # число базовых моделей   
                                   learning_rate=0.1,  # шаг обучения 
                                   subsample=1.0,      # доля случайных объектов для обучения
                                   max_features=1.0)   # доля случайных признаков для обучения
model.fit(X_train, Y_train)       # обучение модели   
Y_hat = model.predict(X_test)     # построение прогнозов
print(f'Точность прогнозов: {100*accuracy_score(Y_test, Y_hat):.1f}%')

P_hat = model.predict_proba(X_test)  # можно предсказывать вероятности классов
loss = brier_score_loss(Y_test, P_hat[:,1])  # мера Бриера на вер-ти положительного класса
print(f'Мера Бриера ошибки прогноза вероятностей: {loss:.2f}')

Градиентный бустинг для регрессии:

from sklearn.ensemble import GradientBoostingRegressor
from sklearn.metrics import mean_absolute_error

X_train, X_test, Y_train, Y_test = get_demo_regression_data()  

# инициализация модели (базовые модели-по умолчанию деревья, но могут быть другие):
model = GradientBoostingRegressor(n_estimators=1000,  # число базовых моделей   
                                  learning_rate=0.1,  # шаг обучения  
                                  subsample=1.0,      # доля случайных объектов для обучения
                                  max_features=1.0)   # доля случайных признаков для обучения     
model.fit(X_train, Y_train)       # обучение модели   
Y_hat = model.predict(X_test)     # построение прогнозов
print(f'Средний модуль ошибки (MAE): \
    {mean_absolute_error(Y_test, Y_hat):.2f}')       

Больше информации. Полный код.

Литература

1. Hastie T., Tibshirani R., Friedman J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction. – Springer Science & Business Media, 2009.