Иллюстрация работы градиентного бустинга по шагам

Рассмотрим визуализацию работы градиентного бустинга:

$$G_m(\mathbf{x})=f_0(\mathbf{x})+\varepsilon f_1(\mathbf{x})+\varepsilon f_2(\mathbf{x})+...+\varepsilon f_m(\mathbf{x}),$$ $$m=1,2,3,...,$$

где

• $f_0(\mathbf{x})\equiv 0$;

• $f_1(\mathbf{x}),f_2(\mathbf{x}),...$ - решающие деревья глубины 3;

• $\varepsilon=0.3$.

Для простоты визуализации рассмотрим двумерное признаковое пространство

$$\mathbf{x}=[x^1,x^2]$$

Будем строить целевую зависимость $y(\mathbf{x})$ и текущее приближение $G_m(\mathbf{x})$ на левом графике, а ошибку $y(\mathbf{x})-G_m(\mathbf{x})$ и следующую базовую модель $f_{m+1}(\mathbf{x})$ - на правом.

$$m=0:$$

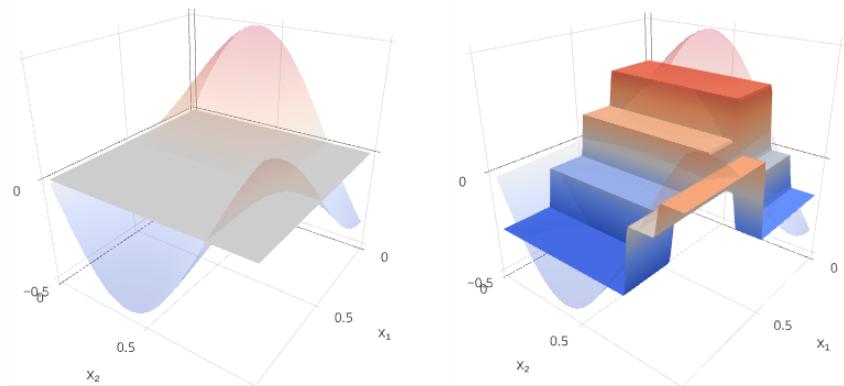
$$m=1:$$

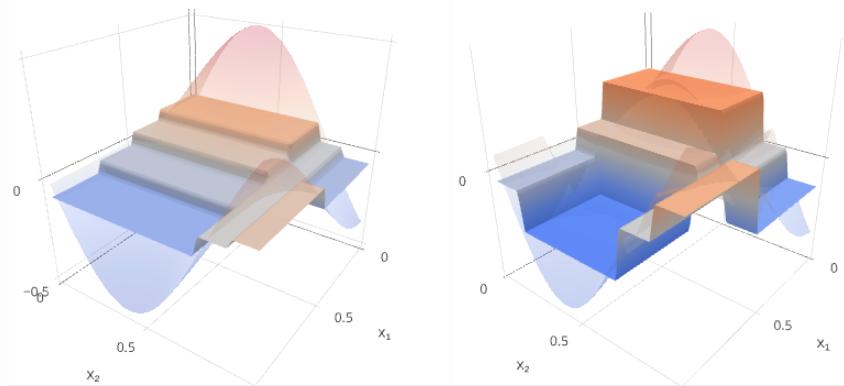
$$m=2:$$

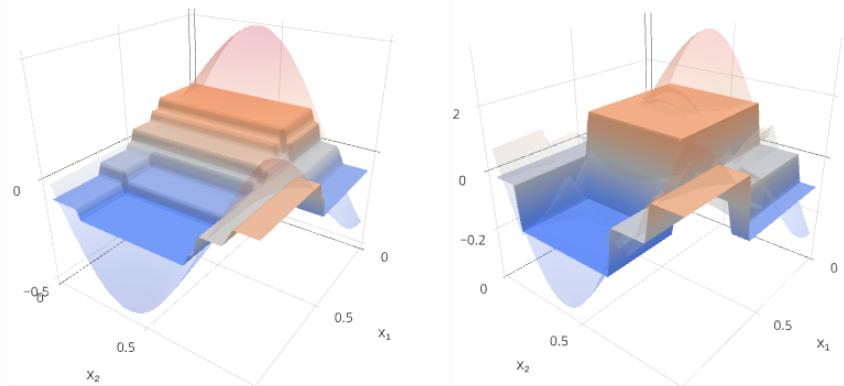
$$m=3:$$

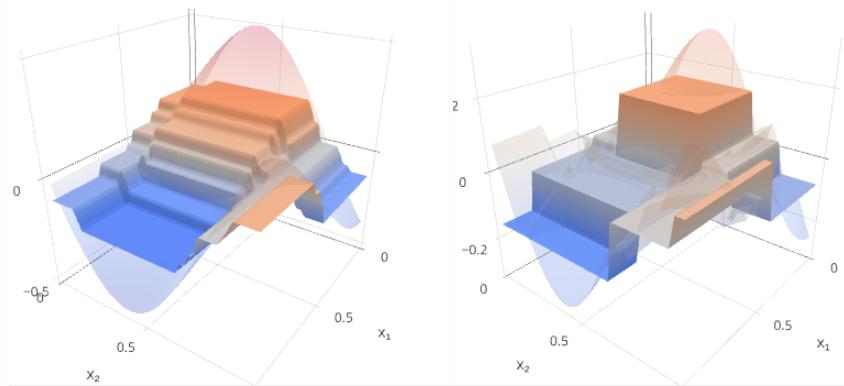
$$m=4:$$

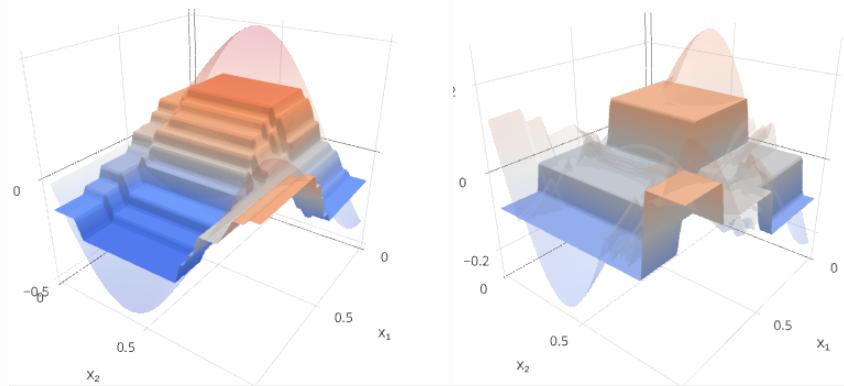
$$m=5:$$

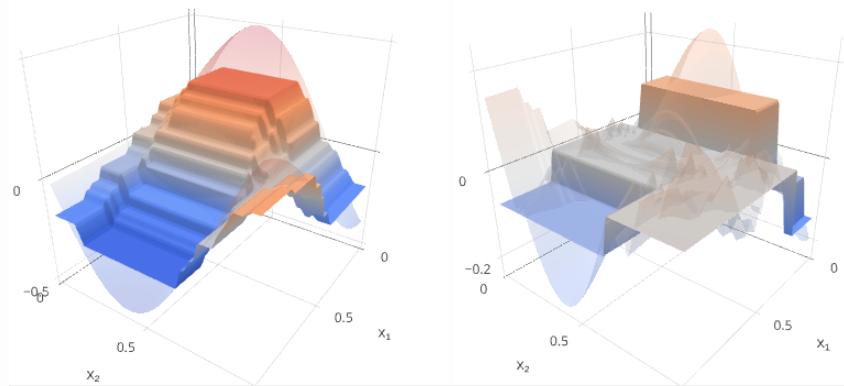
$$m=6:$$

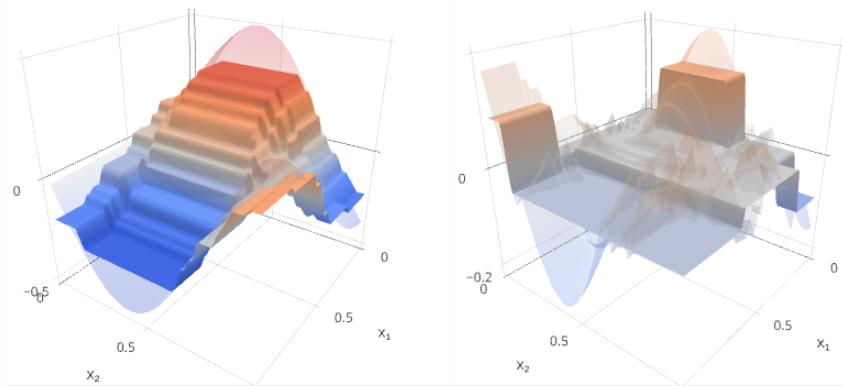
$$m=7:$$

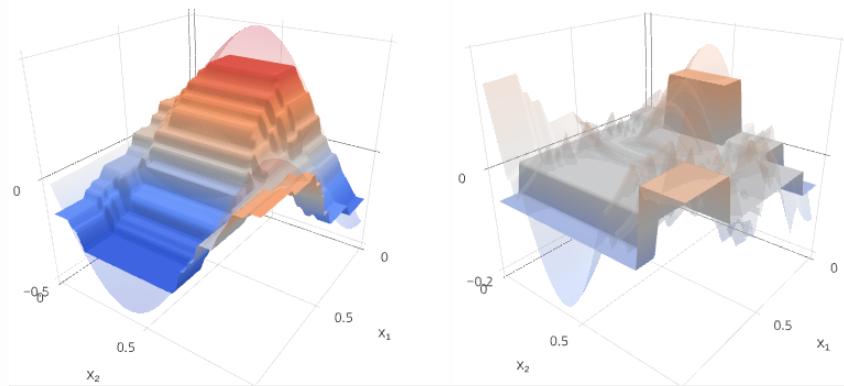
$$m=8:$$

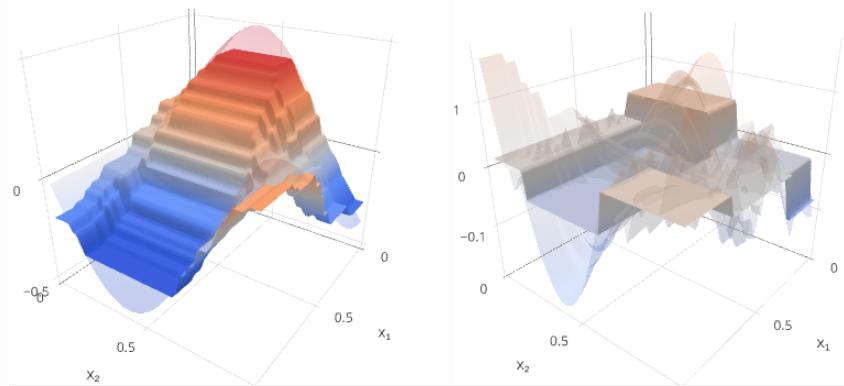
$$m=9:$$

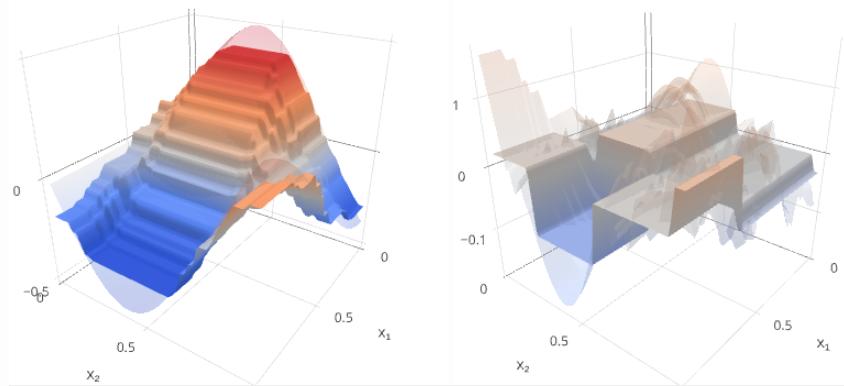
$$m=10:$$

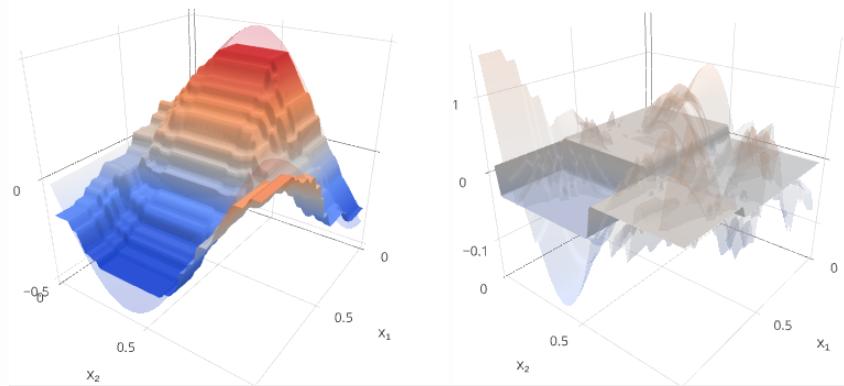
Как видим, с ростом $m$ отклонение прогноза от истинного значения уменьшается и становится более шумным. Скачки в ошибке возникают на местах разбиения признакового пространства узлами деревьев.

Результаты работы были получены, используя интерактивный визуализатор Алексея Рогожникова [1], в котором можно отобразить работу бустинга и при других пользовательских настройках.

Литература

1. Brilliantly wrong: Gradient Boosting explained.